降维算法----PCA原理推导
1、从几何的角度去理解PCA降维
以平面坐标系为例,点的坐标是怎么来的?
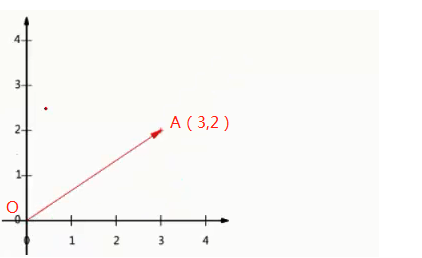
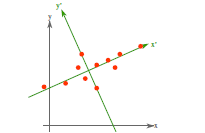
图1 图2
如上图1所示,向量OA的坐标表示为(3,2),A点的横坐标实为向量OA与单位向量(1,0)的内积得到的(也就是向量OA在单位向量(1,0)所表示的的方向上的投影的长度,正负由向量OA与投影方向的夹角决定),纵坐标同理可得。而降维的过程从几何的角度去理解,实质就可以理解为投影的过程。如上图2,二维平面上的点为例,对其降维实际就是将其投影到某一方向上,将二维数据点转换为一维数据点。显然我们可投影的方向有无数多个。并不是随意选择一个方向投影就能满足我们的要求。因为我们降维的最终目的还是为了更好更快捷的分析数据间的规律,如果我们的降维破坏掉了原数据间的规律,那这种对数据的处理是无意义的。那在处理数据时,我们就需要考虑将原始数据往哪里投影的问题?PCA已经帮我们给出了这个问题的答案。
2、PCA原理推导
2.1 最大方差理论(PCA理论基础)
在信号处理中认为信号具有较大的方差,噪声有较小的方差,信噪比就是信号与噪声的方差比,越大越好。如上述图2,样本在x'的投影方差较大,在y'的投影方差较小,那么认为纵轴上的投影是由噪声引起的。因此我们认为,最好的k维特征是将n维样本点转换为k维后,每一维上的样本方差都很大。故我们的投影方向就可以确定为样本数据方差最大的方向。对于高维度的数据,我们的投影方向要选择多个。按照我们的最大方差原理,第一个投影方向为方差最大的方向,第二个方向为方差次大的方向....,直到已经选择的投影方向的数量满足我们的要求。那如果按照这种方式去选择,会存在一个问题,即这些维度之间是近似线性相关的,如果将这些维度从集合中的坐标系去理解。显然由它们所组成的坐标系之家的夹角很小。这样显然不能完全表征数据所有特征。为了让任意两个维度能够尽可能多的表征数据的特征,我们需要选择独立的维度。举例如下:
假如我们现在要将一个具有5个维度的数据,降维到3个维度。
第一步:找到方差最大的方向,选择此方向作为第一个维度
第二步:在于第一步确定的方向正交的方向上,找到方差最大的作为第二个维度
第三步:在与第一步和第二步所选择方向正交的方向上,找到方差最大的作为第三个维度
2.2 PCA数学推导(解释了求解主成分为什么最终是求解协方差矩阵的特征值与特征向量)
如何通过数学去寻找方差最大的方向呢?
第一步:构建线性变换
问题:为什么要对样本进行线性变换?
解答:线性变化的过程应用在此处从几何的角度去理解实为(一)重新确定单位基向量与(二)原始样本集所表示的向量在新的单位基向量上投影的过程;以下述式(4)矩阵形式为例解释如下:
(一)重新确定单位基向量
如下式(4)矩阵中的每一行即为重新确定的单位基向量(p维),类比到二维平面中即就是确定如上文图2中x'和y'
(二)原始样本集所表示的向量在新的单位基向量上投影
如下式(4)中y1,y2到yp即就是数据原始样本集中的每一个样本分别在(一)中所确定的单位基向量上投影所得到的由重新确定的单位基向量所组成的坐标系下的向量每个维度的坐标值。
我们通过下述式(4)就可以表达上述(一)和(二),而(一)中重新确定的基向量要符合方差最大的要求,如何使得其满足方差最大的要求?数学原理即为如下“第二步:求解最大方差”的推导过程
设原样本数据维度为p,则可以写成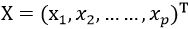 ,这里X表示某一样本数据,设样本集中有N个样本,则样本集的均值方差如下:
,这里X表示某一样本数据,设样本集中有N个样本,则样本集的均值方差如下:

对原样本进行如下线性变换
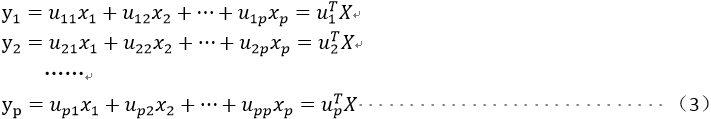
同时给出上述线性变换的矩阵形式如下

第二步:求解最大方差
新的数据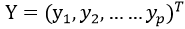 的方差与协方差满足如下式子:
的方差与协方差满足如下式子:
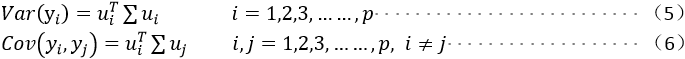
假如我们希望y1的方差达到最大,则显然此问题是一个约束优化问题(二次优化问题)形式如下:

对式(7)的说明,注意这里的u表示的新的坐标系下的基向量(即为上述式(4)中举证的每一行元素组成),限制条件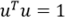 是为了使得基向量是单位向量,即长度为1 。
是为了使得基向量是单位向量,即长度为1 。
关于二次型在约束条件下的极值问题即求解上述式(7)有如下定理:
即在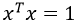 条件下,一般二次型
条件下,一般二次型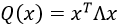 的最大、最小值的求法:
的最大、最小值的求法:
定理1:设Λ是对称矩阵,令m = min{xTΛx:||x||=1},M = max{xTΛx:||x||=1},那么M是Λ的最大特征值λ1,m是Λ的最小特征值,如果x是对应M的单位特征向量u1,那么xTΛx的值为M,如果x是对应m的单位特征向量,xTΛx的值为m;
定理2:设Λ,λ1和u1如定理1所示。在条件xTx=1和xTu1=0限制下xTΛx最大值是第二大特征值λ2,且这个最大值,可以在对应λ2的特征向量u2处取到。
推论:设Λ是一个n*n的对称矩阵,且其正交对角化为Λ=PDP-1,将对角举证D上的元素重新排列,使得λ1 >=λ2 >=……>=λn,且P的列是其对应的单位特征向量u1,u2,……,un,那么对k-2,....n时,在条件xTx=1,xTu1=0,……xTuk=0限制下,xTΛx的最大特征值λk,且这个最大特征值在x=uk处可以取到。
上述定理1,定理2,推论的证明过程见求二次型最大最小值方法初探
由上述式(1)到式(7)的推导过程我们便将求解最大方差的问题转换为了求解协方差矩阵∑的特征值与特征向量。
设u1是∑最大特征值(设为λ1)的特征向量,此时y1为第一主成分,类似的希望y2的方差达到最大,并要求cov(y1,y2)=0,由于u1是λ1的特征向量,所以选择的u2应与u1正交,类似于前面的推导,a2是∑第二大特征值(设为λ2)的特征向量,称y2为第二主成分,依次类推得到后续主成分。
3、PCA降维步骤
由上述2、PCA原理推导,我们已经知晓,求解数据集的主成分的过程即为求解样本集协方差矩阵的特征值与特征向量的过程。
假设数据集为:

第一步:将样本数据中心化(为了简化运算,这部并不是必须的)
上述数据集已完成中心化
第二步:计算样本数据的协方差矩阵

第三步:求出协方差矩阵的特征值与正交单位特征向量
特征值: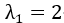 ,对应的特征向量为:
,对应的特征向量为: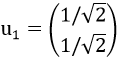
特征值: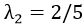 ,对应的特征向量为:
,对应的特征向量为: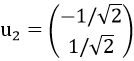
第四步:对上述协方差矩阵对角化
线性代数中定理:对于任意n阶实对称矩阵A,必然存在n阶正交矩阵P,使得: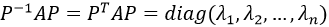 ,其中
,其中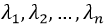 为A的全部特征值;矩阵P为列向量组为A的n个标准正交的特征向量
为A的全部特征值;矩阵P为列向量组为A的n个标准正交的特征向量
由上述定理可知:

最大特征值为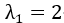 ,对应的特征向量为
,对应的特征向量为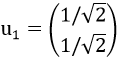 ,故第一主成分为:
,故第一主成分为: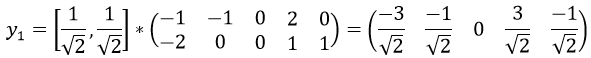
次大特征值为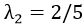 ,对应的特征向量为
,对应的特征向量为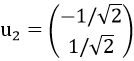 ,故第二主成分为:
,故第二主成分为: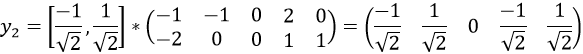
降维算法----PCA原理推导的更多相关文章
- 机器学习实战基础(二十一):sklearn中的降维算法PCA和SVD(二) PCA与SVD 之 降维究竟是怎样实现
简述 在降维过程中,我们会减少特征的数量,这意味着删除数据,数据量变少则表示模型可以获取的信息会变少,模型的表现可能会因此受影响.同时,在高维数据中,必然有一些特征是不带有有效的信息的(比如噪音),或 ...
- 一文彻底搞懂BP算法:原理推导+数据演示+项目实战(上篇)
欢迎大家关注我们的网站和系列教程:http://www.tensorflownews.com/,学习更多的机器学习.深度学习的知识! 反向传播算法(Backpropagation Algorithm, ...
- [机器学习理论] 降维算法PCA、SVD(部分内容,有待更新)
几个概念 正交矩阵 在矩阵论中,正交矩阵(orthogonal matrix)是一个方块矩阵,其元素为实数,而且行向量与列向量皆为正交的单位向量,使得该矩阵的转置矩阵为其逆矩阵: 其中,为单位矩阵. ...
- 机器学习实战基础(二十):sklearn中的降维算法PCA和SVD(一) 之 概述
概述 1 从什么叫“维度”说开来 我们不断提到一些语言,比如说:随机森林是通过随机抽取特征来建树,以避免高维计算:再比如说,sklearn中导入特征矩阵,必须是至少二维:上周我们讲解特征工程,还特地提 ...
- PCA原理推导及其在数据降维中的应用
一个信号往往包含多个维度,各个维度之间可能包含较强的相关性.下图表示的是一组二维信号x=(x1,x2),可以看到数据点基本上分布在x2=x1这条直线上,二者存在很强的相关性(也就是确定x1之后,就能确 ...
- ML: 降维算法-PCA
PCA (Principal Component Analysis) 主成份分析 也称为卡尔胡宁-勒夫变换(Karhunen-Loeve Transform),是一种用于探索高维数据结 ...
- 降维算法-PCA主成分分析
1.PCA算法介绍主成分分析(Principal Components Analysis),简称PCA,是一种数据降维技术,用于数据预处理.一般我们获取的原始数据维度都很高,比如1000个特征,在这1 ...
- 非监督的降维算法--PCA
PCA是一种非监督学习算法,它能够在保留大多数有用信息的情况下,有效降低数据纬度. 它主要应用在以下三个方面: 1. 提升算法速度 2. 压缩数据,减小内存.硬盘空间的消耗 3. 图示化数据,将高纬数 ...
- 机器学习实战基础(二十三):sklearn中的降维算法PCA和SVD(四) PCA与SVD 之 PCA中的SVD
PCA中的SVD 1 PCA中的SVD哪里来? 细心的小伙伴可能注意到了,svd_solver是奇异值分解器的意思,为什么PCA算法下面会有有关奇异值分解的参数?不是两种算法么?我们之前曾经提到过,P ...
随机推荐
- Luogu P4118 [Ynoi2016]炸脖龙I
题目 首先考虑没有修改的情况.显然直接暴力扩展欧拉定理就行了,单次复杂度为\(O(\log p)\)的. 现在有了修改,我们可以树状数组维护差分数组,然后\(O(\log n)\)地单次查询单点值. ...
- 基于MatConvNet的CNN图像搜索引擎PicSearch
简介 Picsearch是一种基于卷积神经网络特征的图像搜索引擎. Github:https://github.com/willard-yuan/CNN-for-Image-Retrieval Web ...
- Docker 添加容器SSH服务
很多时候我们需要登陆到容器内部操作,此时我们就需要开启容器的SSH支持了,下面的小例子将具体介绍三种分配IP地址的方法,分别是pipworl分配,commit分配,Docker分配等. 基于commi ...
- Git复习(三)之分支管理、分支策略
创建合并删除分支 我们知道每次提交git都会将他们串成一条线,这条时间线就是一个分支.在git里这条时间线叫做主分支,即master分支 HEAD指向master,master指向最新的提交,所以,H ...
- Sklearn使用良心完整入门教程
The complete .ipynb file can be download through my share in onedrive:https://1drv.ms/u/s!Al86h1dThX ...
- leetcode 1051. Height Checker
Students are asked to stand in non-decreasing order of heights for an annual photo. Return the minim ...
- 禁止ios10双指缩放
document.addEventListener('gesturestart', function(event) { event.preventDefault(); });
- json串到java对象
json串到java对象 前端传入参数json字符串,格式如下: {"语文":"88","数学":"78"," ...
- 配置maven的国内镜像
pom.xml文件出现错误标记,一般是相关的maven资源没有下载完整. 1,配置maven的国内镜像,保证能够顺利下载maven中配置的资源. 在maven的配置文件 settings.xml ...
- Mybatis常见面试题总结
1.#{}和${}的区别是什么? ${}是Properties文件中的变量占位符,它可以用于标签属性值和sql内部,属于静态文本替换,比如${driver}会被静态替换为com.mysql.jdbc. ...
