洛谷 P2783 有机化学之神偶尔会做作弊(Tarjan,LCA)

题目背景

LS中学化学竞赛组教练是一个酷爱炉石的人。

有一天他一边搓炉石一边监考，而你作为一个信息竞赛的大神也来凑热闹。

然而你的化竞基友却向你求助了。

“第1354题怎么做”<--手语 他问道。

题目描述

你翻到那一题：给定一个烃，只含有单键（给初中生的一个理解性解释：就是一堆碳用横线连起来，横线都是单条的）。

然后炎魔之王拉格纳罗斯用他的火焰净化了一切环（？？？）。所有的环状碳都变成了一个碳。如图所示。

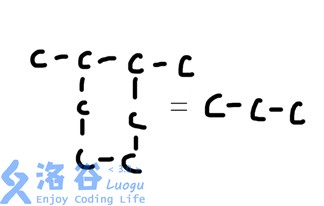
然后指定多组碳，求出它们之间总共有多少碳。如图所示（和上图没有关系）。

但是因为在考试，所以你只能把这个答案用手语告诉你的基友。你决定用二进制来表示最后的答案。如图所示（不要在意，和题目没有什么没关系）。

输入输出格式

输入格式：

第一行两个整数n,m.表示有n个点，m根键

接下来m行每行两个整数u，v表示u号碳和v号碳有一根键

接下来一个整数tot表示询问次数

接下来tot行每行两个整数，a,b表示询问的两个碳的编号

输出格式：

共tot行

每行一个二进制数

输入输出样例

输入样例#1： 复制

3 2
1 2
2 3
2
1 2
2 3

输出样例#1： 复制

10
10

说明

1<n<=10000,1<m<=50000

（两个碳不成环）

这是一道包含了两个板子的题目:tarjan+lca。(应该还是比较明显的)

但是这里我们发现C与C之间必须要连一条双向边，不符合普通tarjan的要求。

我们注意到题目中的条件:两个C不成环。那我们只要让当前的点不递归到它的"爸爸"就可以了。

lca是在树上求两点距离的很常见,常用的办法，在碰到树上题目是可以多考虑。

至于2进制我打的不是很简洁,可以学习一下别人的。

 #include<bits/stdc++.h>
 using namespace std;
 int n,m,cnt,vistime,sum,top;
 int head[],h[],dfn[],low[],s[],num[],deep[],f[][],belong[],ans[];
 bool instack[];
 struct node{
 int to,next;
 }edge[],e[];
 int read()
 {
     int x=,w=;char ch=getchar();
     while(ch>''||ch<'') {if(ch=='-')w=-;ch=getchar();}
     while(ch>=''&&ch<='') x=(x<<)+(x<<)+ch-'',ch=getchar();
     return x*w;
 }
 void add(int x,int y)
 {
     cnt++;
     edge[cnt].to=y;
     edge[cnt].next=head[x];
     head[x]=cnt;
 }
 void ad(int x,int y)
 {
     cnt++;
     e[cnt].to=y;
     e[cnt].next=h[x];
     h[x]=cnt;
 }
 void print(int x)
 {
     int cnt=;
     if(x==) {printf("");return;}
     if(x<) printf("-"),x=-x;
     while(x)
     {
         cnt++;
         if(x&) ans[cnt]=;
         x>>=;
     }
     for(int i=cnt;i>;i--)
     {
         printf("%d",ans[i]);
         ans[i]=;
     }
     printf("\n");
 }
 void tarjan(int,int);
 void build(int,int,int);
 int lca(int,int);
 int main()
 {
     int u,v,tot;
     n=read();m=read();
     for(int i=;i<=m;i++)
     {
         u=read();v=read();
         add(u,v);
         add(v,u);
     }
     cnt=;
     for(int i=;i<=n;i++)
     {
         if(!dfn[i])
         tarjan(i,);
     }
     for(int i=;i<=n;i++)
     {
         for(int j=head[i];j;j=edge[j].next)
         {
             v=edge[j].to;
             if(belong[v]!=belong[i])
             {
                 ad(belong[i],belong[v]);
             }
         }
     }
     build(,,);
     for(int j=;j<=;j++)
     for(int i=;i<=sum;i++)
     {
         f[i][j]=f[f[i][j-]][j-];
     }
     tot=read();
     for(int i=;i<=tot;i++)
     {
         u=read();v=read();
         int LCA=lca(belong[u],belong[v]);
         print(deep[belong[u]]+deep[belong[v]]-*deep[LCA]+);
     }
 }
 void tarjan(int u,int from)//增加参数，防止搜回去
 {
     int v;
     dfn[u]=low[u]=++vistime;
     s[++top]=u;
     instack[u]=true;
     for(int i=head[u];i;i=edge[i].next)
     {
         v=edge[i].to;
         if(v==from) continue;
         if(!dfn[v])
         {
             tarjan(v,u);
             low[u]=min(low[v],low[u]);
         }
         else if(instack[v])
         {
             low[u]=min(low[u],dfn[v]);
         }
     }
     if(dfn[u]==low[u])
     {
         sum++;
         do
         {
             v=s[top--];
             belong[v]=sum;
             num[sum]++;
             instack[v]=false;
         }while(u!=v);
     }
 }
 void build(int k,int fa,int d)
 {
     int v;
     deep[k]=d;
     for(int i=h[k];i;i=e[i].next)
     {
         v=e[i].to;
         if(v!=fa&&!deep[v])
         {
             f[v][]=k;
             build(v,k,d+);
         }
     }
 }
 int lca(int x,int y)
 {
     if(deep[x]>deep[y]) swap(x,y);
     for(int i=;i>=;i--)
     if(deep[f[y][i]]>=deep[x]) y=f[y][i];
     if(x==y) return x;
     for(int i=;i>=;i--)
     {
         if(f[x][i]!=f[y][i])
         x=f[x][i],y=f[y][i];
     }
     return f[x][];
 }