洛谷P1309 瑞士轮——题解

题目传送

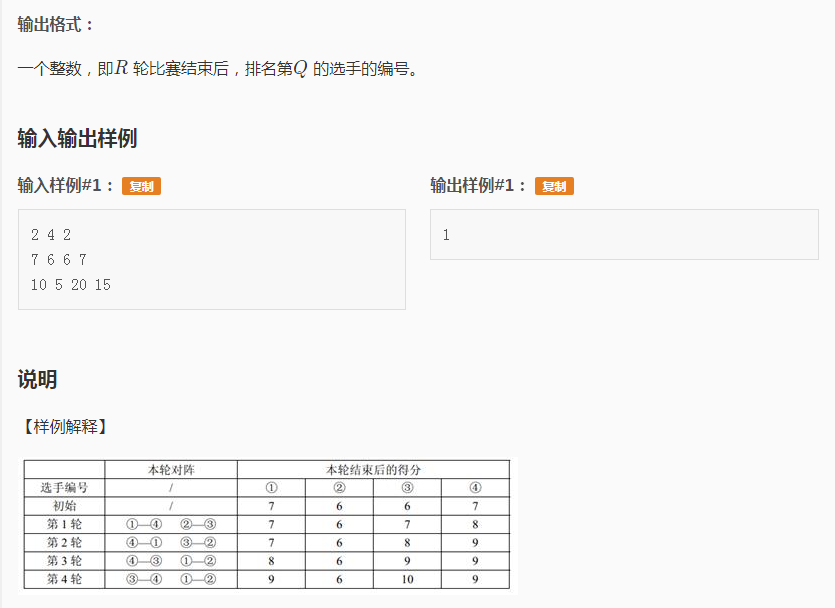
思路非常简单，只要开始时把结构体排个序，每次给赢的加分再排序，共r次，最后再输出分数第q大的就行了。

　　（天真的我估错时间复杂度用每次用sort暴力排序结果60分。。。）实际上这道题估算时间复杂度时O括号里的n并不是输入的n，而是输入的n乘2，这就要求我们精准地估算时间复杂度以采取合适的算法来解题。显然sort时不行的。为什么sort这么强都会TLE？考虑不行的原因，找找有用的教训：（先普及一下：sort是冒泡排序的改进版，平均时间复杂度为O(n log n)，最坏情况下会退化成O(n²)。）

　　从sort的原理开始考虑：sort排序时会有两个指针分别从头到尾相向而行直到相遇后的分手。然后再分别对左右两部分递归，直到递归的区间长度为1。这样发现，就算这个序列已经有序（或基本有序）时，sort会造成大量的时间浪费。这时同时O(n log n)级别的归并排序就不同了。当序列基本有序时，归并排序会造成更少的时间浪费，因为序列基本有序时，“并”操作左右两区间中的左区间应该是主要都小于右区间的，这样就会使左区间更早地并入答案数组，剩下的右区间的长度相应地更长，用个memcpy就完事了，结果是使使左右区间的开头端点比较的次数减少，进而减少了时间浪费。

　　发现把一个大轮回比赛里的所有赢家单独拿出来后他们的顺序都是合法且不变的（因为都是从原来的序列中的相应值加1）；所有输家的大小顺序也是合法的（因为值都没有改变）。这样可以直接用归并排序的思想，把赢家都放在一个区间、输家放在另一个区间中，两个区间只要归并一次就能得到有序的数列了，无需再各种递归费解合并。

见AC代码：

 #include<iostream>
 #include<algorithm>
 #include<cstdio>
 #include<cctype>
 #include<cstring>

 using namespace std;

 struct hum{
     int num,s,w;
 }a[],win[],lose[];//赢的放一起，输的放一起

 int n,r,q,ans,lw,ll;

 char ch;

 bool cmp(hum a,hum b)
 {
     return a.s>b.s||(a.s==b.s&&a.num<b.num);
 }

 inline int read()
 {
     ans=;
     ch=getchar();
     while(!isdigit(ch)) ch=getchar();
     while(isdigit(ch)) ans=(ans<<)+(ans<<)+ch-'',ch=getchar();
     return ans;
 }

 int main()
 {
        n=(read())<<,r=read(),q=read();
     for(int i=;i<=n;i++)
     {
         a[i].num=i;
         a[i].s=read();
     }
     for(int i=;i<=n;i++)    a[i].w=read();
     sort(a+,a+n+,cmp);
     for(int k=;k<=r;k++)
     {
         for(int i=;i<=n;i+=)
         {
             if(a[i].w>a[i+].w)
             {
                 a[i].s++;
                 win[++lw]=a[i];
                 lose[++ll]=a[i+];
             }
             else
             {
                 a[i+].s++;
                 win[++lw]=a[i+];
                 lose[++ll]=a[i];
             }
         }
         int l=,r=,len=;//往下都是并的过程
         while(l<=lw&&r<=ll)
         {
             if(win[l].s>lose[r].s)
                 a[len++]=win[l++];
             if(win[l].s<lose[r].s)
                 a[len++]=lose[r++];
             if(win[l].s==lose[r].s)
             {
                 if(win[l].num<lose[r].num) a[len++]=win[l++];
                 else a[len++]=lose[r++];
             }
         }
         if(l<=lw) memcpy(a+len,win+l,sizeof(hum)*(lw-l+));
         if(r<=ll) memcpy(a+len,lose+r,sizeof(hum)*(ll-r+));//并的过程结束
         lw=;ll=; //因为是由前缀++维护，所以要初始化为1
     }
     cout<<a[q].num;
     return ;
 }

还是要做好时间复杂度估计的说！