[CSP-S模拟测试]:attack（支配树+LCA+bitset）

题目传送门（内部题55）

---

输入格式

第一行，包含两个整数：$n,m,q$，表示敌军城市数、路数和情报数。
接下来$m$行，每行包含两个整数：$u,v$，表示从$u$到$v$包含一条单向道路。
接下来$q$行，每行包含一些整数：$k\ u_1\ u_2...u_k$，表示敌军会向$u_1...u_k$这$k$个城市派遣大军。

---

输出格式

对于每个询问，输出一行包含一个整数表示必经的城市数。

---

样例

样例输入1：

4 3 2
1 2
2 3
2 4
2 3 4
2 2 4

样例输出1：

2
2

样例输入2：

4 4 1
1 2
1 3
2 4
3 4
1 4

样例输出2：

---

数据范围与提示

样例$1$解释：

两个询问的必经点为：$1,2$

样例$2$解释：

询问的必经点为：$1,4$

数据范围：

对于$10\%$的数据，$1\leqslant n\leqslant 7,1\leqslant m\leqslant 10,1\leqslant q\leqslant 100$；
对于$40\%$的数据，$1\leqslant n\leqslant 50,000,m=n-1,1\leqslant q\leqslant 100,000$；
对于$100\%$的数据，$1\leqslant n\leqslant 50,000,1\leqslant m\leqslant 100,000,1\leqslant q\leqslant 100,000,\sum k\leqslant 100,000$。

---

题解

首先，想吐槽一下出题人，下面是官方题解中的第一句话：

可能是因为我的语文真的不好，反正我是没看出来是$DAG$，然而就因为这个打乱了我整场考试的节奏。

两种解法，我们一一道来：

$1.$支配树：

支配树板子题，简单讲一下

对于$40\%$的数据，是一棵树，我们无非就是求出$k$个数的$lca$，然后$depth[lca]$就是答案。

那么我们现在考虑不是一棵树的情况，就像样例$2$，会是类似下面的一张图：

对于点$6$，从$1$到它的必经点就是$1,2,5,6$，那么我们考虑如何求出这个答案。

对于$DAG$，我们就考虑$topsort$。

还是考虑利用树的情况的$depth[lca]$，那么我们就是想办法将$5$的直接父亲设为$2$即可。

思考一下下面的操作：

　　$\alpha.$如果一个点第一次被访问，那么就现将它的父亲设为指向它的点；如上图中，相当于$3\sim 5$和$4\sim 5$都没有被经过过，现在我们走了$3\sim 5$这条边，然后我们先将$5$的直接父亲设为$3$。

　　$\beta.$如果这个点已经被访问过了，那么我们将它的直接父亲设为现在指向它的这个点和现在所记录的这个点的直接父亲的$lca$；如上图中，相当于我们已经经过了$3\sim 5$这条边，然而还没有经过过$4\sim 5$这条边，现在我们走了$4\sim 5$这条边，然后我们要将$5$这个点的直接父亲设置为$3$和$4$的$lca$，即为$2$号点。

而对于上面这张图，你可以将其理解为我们将其变为了下图：

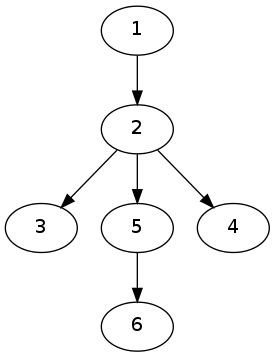
重复上面的操作，直到完成整个$topsort$，我们也就相当于将其变成了一棵树，也就转化成了$40\$数据的解法。

时间复杂度：$\Theta(k\log n)$。

期望得分：$100$分。

实际得分：$100$分。

$2.bitset$：

这个就很简单了，无非就是利用$bitset$记录一下必须经过的点，还是分为两种情况：

　　$\alpha.$还没有被访问过，直接将指向它的点的$bitset$传给它，不要忘了它自己。

　　$\beta.$被访问过，那么将它的$bitset$与指向它的$bitset$取$\&$即可。

注意空间问题，需要将$bitset$开一半，然后先处理编号前$25000$的点，然后再处理编号后$25000$号点，否则空间会超；答案就是两次处理出来的$.count()$的和。

时间复杂度：$\Theta(\frac{k\times n}{32})$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

支配树：

#include<bits/stdc++.h>
using namespace std;
struct rec{int nxt,to;}e[100001];
int head[50001],cnt;
int n,m,q,k;
int du[50001];
int depth[50001],fa[50001][21];
int que[50001];
void add(int x,int y)
{
	e[++cnt].nxt=head[x];
	e[cnt].to=y;
	head[x]=cnt;
}
int LCA(int x,int y)
{
	if(depth[x]<depth[y])swap(x,y);
	for(int i=20;i>=0;i--)
		if(depth[fa[x][i]]>=depth[y])x=fa[x][i];
	if(x==y)return x;
	for(int i=20;i>=0;i--)
		if(fa[x][i]!=fa[y][i])
		{
			x=fa[x][i];
			y=fa[y][i];
		}
	return fa[x][0];
}
void topsort()
{
	que[1]=depth[1]=1;
	int h=0,t=1;
	while(h<=t)
	{
		h++;
		depth[que[h]]=depth[fa[que[h]][0]]+1;
		for(int i=1;i<=20;i++)
			fa[que[h]][i]=fa[fa[que[h]][i-1]][i-1];
		for(int i=head[que[h]];i;i=e[i].nxt)
		{
			if(!fa[e[i].to][0])fa[e[i].to][0]=que[h];
			else fa[e[i].to][0]=LCA(fa[e[i].to][0],que[h]);
			du[e[i].to]--;
			if(!du[e[i].to])que[++t]=e[i].to;
		}
	}
}
int main()
{
	scanf("%d%d%d",&n,&m,&q);
	for(int i=1;i<=m;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		add(x,y);du[y]++;
	}
	topsort();
	while(q--)
	{
		int lca;
		scanf("%d%d",&k,&lca);
		k--;while(k--)
		{
			int x;
			scanf("%d",&x);
			lca=LCA(lca,x);
		}
		printf("%d\n",depth[lca]);
	}
	return 0;
}

$bitset$：

#include<bits/stdc++.h>
using namespace std;
struct rec{int nxt,to;}e[100001];
int head[50001],cnt;
int n,m,q;
int du[2][50001];
int que[50001];
int k[100001];
int ans[100001];
bool vis[50001];
vector<int> question[100001];
bitset<25000> bit[50001],flag;
void add(int x,int y)
{
	e[++cnt].nxt=head[x];
	e[cnt].to=y;
	head[x]=cnt;
}
void topsort1()
{
	que[1]=1;
	int h=0,t=1;
	while(h<=t)
	{
		h++;
		if(que[h]<=25000)bit[que[h]][que[h]]=1;
		for(int i=head[que[h]];i;i=e[i].nxt)
		{
			if(vis[e[i].to])bit[e[i].to]&=bit[que[h]];
			else
			{
				bit[e[i].to]=bit[que[h]];
				vis[e[i].to]=1;
			}
			du[0][e[i].to]--;
			if(!du[0][e[i].to])
				que[++t]=e[i].to;
		}
	}
}
void topsort2()
{
	que[1]=1;
	int h=0,t=1;
	while(h<=t)
	{
		h++;
		if(que[h]>25000)bit[que[h]][que[h]-25000]=1;
		for(int i=head[que[h]];i;i=e[i].nxt)
		{
			if(vis[e[i].to])bit[e[i].to]&=bit[que[h]];
			else
			{
				bit[e[i].to]=bit[que[h]];
				vis[e[i].to]=1;
			}
			du[1][e[i].to]--;
			if(!du[1][e[i].to])
				que[++t]=e[i].to;
		}
	}
}
int main()
{
	scanf("%d%d%d",&n,&m,&q);
	for(int i=1;i<=m;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		add(x,y);
		du[0][y]++;
		du[1][y]++;
	}
	topsort1();
	for(int i=1;i<=q;i++)
	{
		int x;scanf("%d%d",&k[i],&x);
		question[i].push_back(x);
		flag=bit[x];
		for(int j=2;j<=k[i];j++)
		{
			scanf("%d",&x);
			flag&=bit[x];
			question[i].push_back(x);
		}
		ans[i]=flag.count();
	}
	for(int i=1;i<=50000;i++)bit[i]&=0;
	memset(vis,0,sizeof(vis));
	topsort2();
	for(int i=1;i<=q;i++)
	{
		flag=bit[question[i][0]];
		for(int j=1;j<k[i];j++)
			flag&=bit[question[i][j]];
		printf("%d\n",ans[i]+flag.count());
	}
	return 0;
}

---

rp++