[CSP-S模拟测试]:超级树（DP）

题目传送门（内部题5）

---

输入格式

一行两个整数$k$、$mod$，意义见上。

---

输出格式

一行一个整数，代表答案。

---

样例

样例输入1：

2 100

样例输出1：

9

样例输入2：

3 1000

样例输出2：

245

样例输入3：

20 998244353

样例输出3：

450500168

---

数据范围与提示

样例解释：
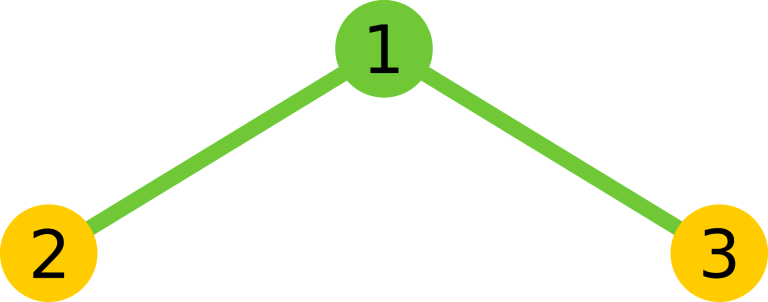
对于第一组样例，将节点如图编号，共有9条不同的路径：1,2,3,1-2,2-1,1-3,3-1,2-1-3,3-1-2。

限制与约定：

对于$10\%$的数据，$k \leqslant 4$。
对于$40\%$的数据，$k \leqslant 10$。
对于$60\%$的数据，$k \leqslant 100$。
另有$10\%$的数据，$mod=998244353$。
对于所有数据，$1 \leqslant k \leqslant 300,1 \leqslant mod \leqslant {10}^9$。

---

题解

有谁能想到$DP$？举个爪

显然k-超级树是由两个$(k-1)-$超级树合在一起加了个根组成的。

那么好吧，确定了是个$DP$，但是又有谁能想到$DP$的意义呢？

定义$dp[i][j]$表示一棵$i-$超级树，有$j$条没有公共点的路径的方案数。

好像说的有点乱，那么我们拿样例来唠两句：

$dp[2][1]=9$，这很显然，就是样例解释中那$9$种方案。

$dp[2][2]=7$，这七种方案分别是$(1,2)$，$(1,3)$，$(2,3)$，$(2,1-3)$，$(2,3-1)$，$(3,1-2)$，$(3,2-1)$。

$dp[2][3]=1$，这种方案是$(1,2,3)$。

$dp[2][4]=0$，因为一共只有$3$个点，所以我们找不到方案了。

现在开始来推式子吧～

我们来考虑$dp[i]$对$dp[i+1]$的贡献：枚举左子树的路径条数l和有子树的路径条数$r$，记$num=dp[i][l] \times dp[i][r]$。

转移分一下五种情况：

　　$1.$什么也不做：$dp[i+1][l+r]+=num$。

　　$2.$跟自己作为一条新路径：$dp[i+1][l+r+1]+=num$，不要忘了根本身还有一条。

　　$3.$根连接到左子树（或右子树）的某条路径上：$dp[i+1][l+r]+=2 \times num \times (l+r)$。

　　　　对于$3$的理解：从左子树里选一条边，延长其终点，连接根的路径条数为$sum \times l$；同理，将起点做如上操作，路径条数也为$sum \times l$；再同理，右子树也是这种操作，路径条数为$2 \times sum \times r$；总的路径条数即为：$dp[i+1][l+r]+=2 \times num \times (l+r)$。

　　$4.$根连接左子树和右子树的各一条路径：$dp[i+1][l+r-1]+=2 \times num \times l \times r$。

　　　　对于$4$的理解：从左子树中选一条边，延长其终点，经根节点连向有子树中一条边的起点，路径条数为：$sum \times l \times r$；同理，从右子树中选一条边也是如此，总的路径条数为：$dp[i+1][l+r-1]+=2 \times num \times l \times r$。

　　$5.$根连接左子树（或右子树）的两条路径：$dp[i+1][l+r-1]+=num \times (l \times (l-1)+r \times (r-1))$。

　　　　对于$5$的理解：左子树中选一条边的终点连向根节点，再将这条边继续延长，连向做字数中另外一条边的起点，路径条数为：$num \times (l \times (l-1))$；右子树中也是如此，路径条数为：$num \times (r \times (r-1))$；总的路径条数即为：$dp[i+1][l+r-1]+=num \times (l \times (l-1)+r \times (r-1))$。

边界为$dp[1][0]=dp[1][1]=1$，答案为$dp[k][1]$。

看起来第二维状态可能有$2^k$那么大，但注意到从$dp[i]$转移到$dp[i+1]$时，路径的条数最多减少1条，因此第二维只有$k$个状态对最终的状态有影响，只$dp$这些状态即可。

时间复杂度$O(k^3)$。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int k;
long long mod,num;
long long dp[310][310];
int main()
{
	dp[1][0]=dp[1][1]=1;
	scanf("%d%lld",&k,&mod);
    for(int i=1;i<k;i++)
		for(int l=0;l<=k-i+1;l++)
    	    for(int r=0;r<=k-i-l+2;r++)
			{
            	num=dp[i][l]*dp[i][r]%mod;
           		dp[i+1][l+r]=(dp[i+1][l+r]+num)%mod;//情况1
           		dp[i+1][l+r+1]=(dp[i+1][l+r+1]+num)%mod;//情况2
           		dp[i+1][l+r]=(dp[i+1][l+r]+2*num*(l+r))%mod;//情况3
           		dp[i+1][l+r-1]=(dp[i+1][l+r-1]+2*num*l*r)%mod;//情况4
           		dp[i+1][l+r-1]=(dp[i+1][l+r-1]+num*(l*(l-1)+r*(r-1)))%mod;//情况5
			}
	printf("%lld",dp[k][1]%mod);
	return 0;
}

---

rp++