遗传算法，实数编码的交叉操作之SBX（模拟二进制交叉）

本文主要介绍遗传算法（实数编码）的交叉操作中的SBX，模拟二进制交叉。

首先，给出个人用python2.7实现的代码，具体模块已上传到：

https://github.com/guojun007/sbx_cross

 #!/usr/bin/env python
 #encoding:UTF-8
 import numpy as np
 import random

 """
     SBX 模拟二进制交叉

 输入：
     population 种群矩阵
     alfa 交叉概率
     numRangeList 决策变量的上限(下限默认为0)
     mu    SBX方式的分布指数, 推荐为1
 """
 def cross(population, alfa, numRangeList, mu=1):
     N=population.shape[0]
     V=population.shape[1]
     populationList=range(N)

     for _ in xrange(N):
         r=random.random()

         if r<alfa:
             p1, p2=random.sample(populationList, 2)
             bq=np.array([0]*V)
             randList=np.random.random(V)
             #根据概率向量判断不同概率函数的选择
             orTF=(randList<=0.5)

             #计算不同决策变量的 不同概率选择 下的 系数
             for j in xrange(V):
                 if orTF[j]==True:
                     bq[j]=(2.0*randList[j])**(1.0/(mu+1))
                 else:
                     bq[j]=(1.0/(2.0*(1-randList[j])))**(1.0/(mu+1))

             #取出选定的两个个体
             old_p1=population[p1, ]
             old_p2=population[p2, ]
             #计算交叉后的两个新个体
             new_p1=0.5*((1+bq)*old_p1+(1-bq)*old_p2)
             new_p2=0.5*((1-bq)*old_p1+(1+bq)*old_p2)

             #上下限判断,防止越界
             new_p1=np.max(np.vstack((new_p1, np.array([0]*V))), 0)
             new_p1=np.min(np.vstack((new_p1, numRangeList)), 0)       

             new_p2=np.max(np.vstack((new_p2, np.array([0]*V))), 0)
             new_p2=np.min(np.vstack((new_p2, numRangeList)), 0)       

             #将交叉后的个体更新回种群
             population[p1, ]=new_p1
             population[p1, ]=new_p2

 ###以下是测试用例
 if __name__=="__main__":
     random.seed(0)
     np.random.seed(0)
     xN=20
     yN=3
     alfa=0.9
     population=np.random.rand(xN*yN).reshape(xN, yN)*1.0

     ###运行函数
     print population
     print '-'*50
     cross(population, alfa, np.array([1]*3))
     print '-'*50
     print population

以下内容引至：

http://blog.csdn.net/silence1214/article/details/48802317

最近在做作业遇到一个Dejong’s fifth function的multi modal的问题，用传统的GA方法尝试了很多次，的确没办法搞定，随机很多次也不一定在global optimum的地方得到一次解。前几天去导师家里的路上谈到这个事情，导师说一般现在都用SBX和polynomial的mutation。于是回来找了相关论文来看，找到了SBX最早的论文，奇怪的是，在论文中竟然没有给出伪代码，只是在讲解他的motivation。大概的motivation是这样的： 
1：SBX主要是用于real number的编码问题，但是借鉴与来自binary 编码的idea。在binary中，假设2个parent分别为p1和p2，后代分别为c1和c2。那么是这么一个属性的：(p1+p2)/2=(c1+c2)/2。再定义一个叫做spread factor的玩意β=|(c2−c1)/(p2−p1)|

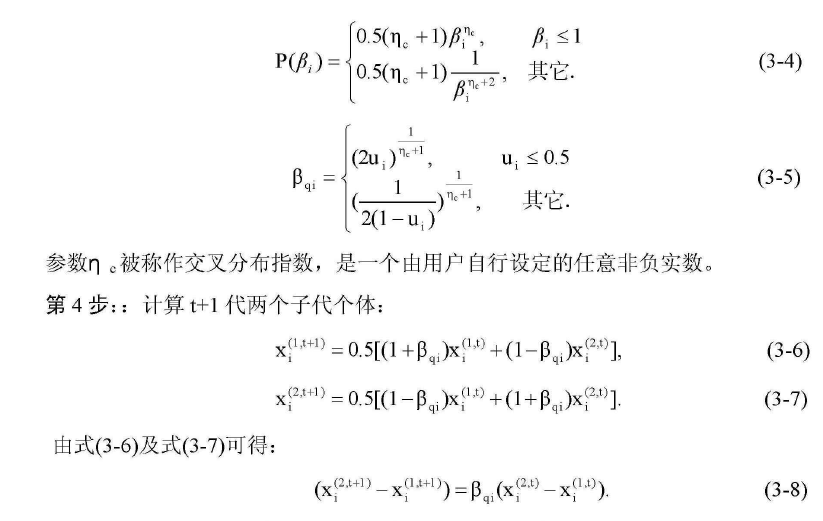
2：在SBX中就要满足第一个属性，以及尽量β也binary中的概率分布一致。由此一个方案： 
c1=(p2+p1)−0.5∗β(p2−p1) 
c2=(p2+p1)+0.5∗β(p2−p1) 
大家可以自己计算，是满足上面2个玩意的。

3：那么接下来其实就是求β的，因为是要让在real的问题中的β的分布尽量接近binary中的，那么就要首先知道binary中的分布。binary中的分布如下： 
c(β)=0.5(n+1)βn,β≤1 and c(β)=0.5(n+1)1βn+2,β>1 
也就是说β有2个分布的，具体怎么做呢？我看到有人实现是这么来的。

3.1：随机一个数字在[0,1]之间，如果该数字小于等于0.5按照第一个来求，否则按照第二个来求。求解的时候是按照对β的概率分布等于这个随机数字来计算的。这个只需要求积分即可，手工就能推导出来。

最后我用这个方法再加上tournament selection以及polynomial mutation的方法，在求解上面说的multi modal的问题的时候，竟然很多次都求解出来了！