Topology and Geometry in OpenCascade-Face

Topology and Geometry in OpenCascade-Face

摘要Abstract：本文简要介绍了几何造型中的边界表示法（BRep），并结合程序说明OpenCascade中的边界表示的具体实现，即拓朴与几何的联系。对具有几何信息的拓朴结构顶点（vertex）、边（edge）、面（face）进行了详细说明。本文仅对面（Face）进行说明。

关键字Key Words：OpenCascade、BRep、Topology、Geometry、Face

一、引言 Introduction

面（Face）由一个外环和若干个内环来表示，内环完全在外环之内。根据环（Wire）的定义，在面上沿环的方向前进，左侧总在面内，右侧总在面外。面有方向性，一般用其外法矢方向作为该面的正向。若一个面的法矢向外，称为正向面；反之，称为反向面。面的形状（surface）由面的几何信息来表示，可以是平面或曲面，平面可用平面方程来描述，曲面可以用控制多边形或型值点来描述（NURBS曲面），也可用曲面方程（隐式、显式或参数形式）来描述。对于参数曲面，通常在其二维参数域上定义环，这样就可以由一些二维的有向边来表示环，集合运算中对面的分割也可在二维参数域上进行。

OpenCascade中的面结构如下图所示：

Figure 1.1 OpenCascade Face

根据其类图可知，面除了其参数曲面mySurface外，还包含显示曲面的剖分（由三角形组成）。当面在着色显示模式下时会计算出面的三角形。可视化的算法是由BRepMesh::Mesh()来为每个面三角剖分后用来显示。

二、面 Face

面（Face）是用来描述三维实体边界的拓朴实体。面是由底层的曲面及一个或多个环（Wire）来描述。例如，一个圆柱体包含三个面：底面、顶面和侧面。每个面都是无限的（无界的）（Geom_Plane和Geom_CylindricalSurface），通过边界来限定无限的面得到面。即用位于Geom_Circle上的边形成的环，限定出底面和顶面。侧面包含四条边：其中两条边与顶面和底面其享，剩下的两条边是缝合边（seam edge），参看之前的讨论。限定侧面的环包含缝合边两次，两个缝合边具有不同的朝向。

2.1 曲面 Surface

让我们简要回顾一下什么是曲面（surface）。如果你在高中时学过数学分析（mathematical analysis），那么你可能对这个概念已经熟记于心。如果没学过，那么可能需要读些文章来自学。在wikipedia上有关于参数曲面的简单例子。

曲面将二维参数空间{u, v}映射到三维空间。如下图所示：

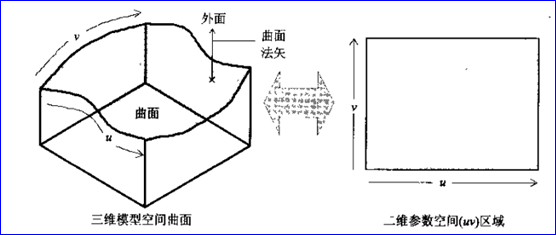
Figure 2.1 Map parameter space{u, v} into 3D space

参数区间可以有界，也可以是无界的，也可以只在一个方向上有界。如平面（Plane）的参数空间是无界的；NURBS是有界的；圆柱面（Cylindrical Surface）在U方向上有界（U∈[0，2π]），在V方向上是无界的。

Geom_Surface::Value()返回一个对应于参数空间中的参数（U，V）的空间点（X，Y，Z）。例如：地球上的任意一点都由纬度（V）和经度（U）表示，但是在世界坐标系中可以看作三维点（假如地球的中心定义为原点）。这个函数是纯虚函数，所有派生自Geom_Surface的类都有对这个函数的实现，使计算各种曲面上对应参数的空间点的方式统一。

让我们回想一下，边必须具有三维曲线（3D Curve）和曲面空间中的参数曲线（pcurve）。而OpenCascade要求面的边界（环wire）在三维和二维空间中必须是闭合的。因此，圆柱的侧面是采用前面我们讨论的那样来描述的。

2.2 朝向 Orientation

面的朝向表示面的法向与曲面法向之间的关系（Face orientation shows how face normal is aligned with its surface normal）。若面的朝向是TopAbs_FORWARD（向前），则面的法向与曲面的法向一致；若面的朝向是TopAbs_REVERSED（反向），则面的法向与曲面的法向相反。面的法向表示材质的位置，材料位于面的背面。在正确描述的实体中，所有面的法向都是向外的，如下图所示：

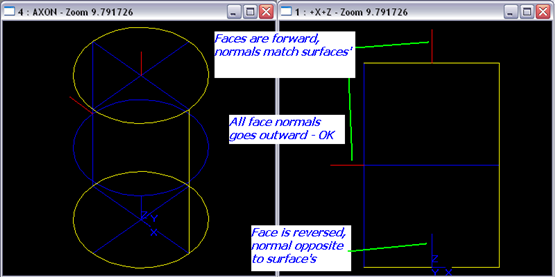
Figure 2.2 In a correct solid body all face normals go outward

面上的材料是由边的朝向确定的。方向是由曲面不是面（）的法向和边的微分的叉积确定。若边的朝向向前，则边的导数等于它的三维曲线的导数；若边的朝向反向，则边的导数与它的三维曲线的导数相反。也许考虑边的参数曲线会更易于理解：假如边是向前的，材料在它的左侧，假如是反向的，则材料在它的右侧。这让我想起了格林公式中对平面区域的边界曲线正向的规定：对平面区域D的边界曲线L，我们规定L的正向如下：当观察者沿L的这个方向行走时，D内在他附近处的那一部分总在他的左边。

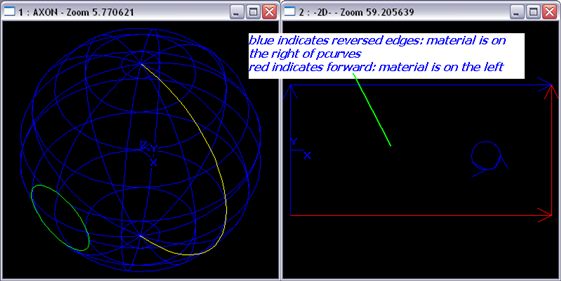
Figure 2.3 Orientation of the edge

当用积分区域的概念来理解边的朝向时好像要容易些。把参数空间看作积分区域D，其中蓝色的边表示材料在参数曲线的右侧；红色的边表示材料在边的左侧。

2.3 容差 Tolerance

面的容差的几何意义是包围面的一个具有厚度的板。如下图所示：

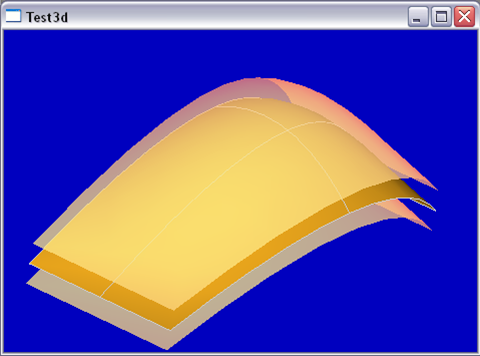
Figure 2.4 Face Tolerance

与边和顶点的容差相比，建模算法中用到面的容差的情况相对要少。通常都使用默认值Precision::Confusion()。通常情况下，OpenCascade要求注意以下条件：

当边位于面上，顶点位于边上时，面的容差<=边的容差<=顶点的容差。

2.4 三角剖分 Triangulation

除了面的参数表示，为了面的显示，需要对面进行三角剖分，剖分得到的三角形也保存在面的数据结构中。当在着色渲染模式下时，可视化算法内部调用了BRepMesh::Mesh()来对每个面进行三角剖分，并将三角剖分得到的三角形加到面的数据结构中。

2.5 附加位置 Additional location

与边和顶点不同，面有附加位置信息（TopLoc_Location），它是面（BRep_TFace）的成员变量。所以，在使用底层曲面或三角剖分得到的三角形时，不要忘了将其考虑进去。

三、示例程序 Example Code

3.1 底层创建面并访问其数据 Creating a face bottom-up and accessing the data

与创建边和顶点一样，需要类BRep_Builder和Brep_Tool来从底层创建面和访问面中的数据。代码如下所示：

BRep_Builder aBuilder;

TopoDS_Face aFace;

aBuilder.MakeFace (aFace, aSurface, Precision::Confusion());

...

TopLoc_Location aLocation;

Handle(Geom_Surface) aSurf = BRep_Tool::Surface (aFace, aLocation);

gp_Pnt aPnt = aSurf->Value (aU, aV).Transformed (aLocation.Transformation());

//or to transform a surface at once

//Handle(Geom_Surface) aSurf = BRep_Tool::Surface (aFace);

//gp_Pnt aPnt = aSurf->Value (aU, aV);

Handle(Poly_Triangulation) aTri = BRep_Tool::Triangulation (aFace, aLocation);

aPnt = aTri->Nodes.Value (i).Transformed (aLocation.Transformation());

一定要考虑面的附加位置信息。

四、结论 Conclusion

面是边界表示法BRep中有几何数据的最后一个拓朴结构。为了面的显示，需要对其进行三角剖分，三角剖分后的数据也是保存在面的数据结构中。面还有附加位置数据需要考虑，若不考虑附加位置，剖分后的三角形都是相对于原点的。

从底层创建面和访问面的属性数据，与顶点和边一样，使用类BRep_Builder和类BRep_Tool来实现。

五、参考资料

1. Roman Lygin, OpenCascade notes, opencascade.blogspot.com

2. 孙家广等. 计算机图形学. 清华大学出版社

3. OpenCascade source code.

PDF Version: Topology and Geometry in OpenCascade-Face