[BZOJ]1059 矩阵游戏(ZJOI2007)

　　虽然说是一道水题，但小C觉得还是挺有意思的，所以在这里mark一下。

Description

　　小Q是一个非常聪明的孩子，除了国际象棋，他还很喜欢玩一个电脑益智游戏——矩阵游戏。矩阵游戏在一个N*N黑白方阵进行（如同国际象棋一般，只是颜色是随意的）。每次可以对该矩阵进行两种操作：行交换操作：选择矩阵的任意两行，交换这两行（即交换对应格子的颜色）列交换操作：选择矩阵的任意行列，交换这两列（即交换对应格子的颜色）游戏的目标，即通过若干次操作，使得方阵的主对角线(左上角到右下角的连线)上的格子均为黑色。对于某些关卡，小Q百思不得其解，以致他开始怀疑这些关卡是不是根本就是无解的！！于是小Q决定写一个程序来判断这些关卡是否有解。

Input

　　第一行包含一个整数T，表示数据的组数。接下来包含T组数据，每组数据第一行为一个整数N，表示方阵的大小；接下来N行为一个N*N的01矩阵（0表示白色，1表示黑色）。

Output

　　输出文件应包含T行。对于每一组数据，如果该关卡有解，输出一行Yes；否则输出一行No。

Sample Input

　　2
　　2
　　0 0
　　0 1
　　3
　　0 0 1
　　0 1 0
　　1 0 0

Sample Output

　　No
　　Yes

HINT

　　对于100%的数据，N ≤ 200。

Solution

　　拿到这道题目肯定要思考，什么样的局面通过交换行列可以变成主对角线上都为黑格的情况？

　　由于交换是可逆的，我们倒过来思考，主对角线上都是黑格的情况通过交换行列可以变成什么局面。

　　这样就一目了然了。一开始是1~n的排列，每次交换行列相当于交换两个位置上的数字。

　　这样问题就转化成：是否能从每行选出恰好一个黑格，n行黑格代表的列数正好组成一个1~n的全排列。

　　正解是二分图匹配。全排列可以看作是行和列的匹配，思路很清晰。时间复杂度O(n^2)（匈牙利算法）/O(n^1.5)（网络流）。

　　但是小C这里要介绍的，是另一种做法。

　　想到矩阵和排列，我们会很自然地想起行列式。

　　我们思考一下行列式的计算公式：。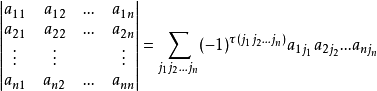

　　发现如果一个排列上的所有数都不为0，就一定会对答案有贡献！

　　所以我们就直接求这个矩阵的行列式的值就可以了？？？复杂度O(n^3)。

　　当然不行，这些排列对答案的贡献有正有负，矩阵的值全为0或1的话很容易凑出0。例如{{0,1,1},{0,1,1},{1,0,0}}。

　　那怎么办？

　　很简单啊，我们给矩阵里的黑格都随机一个权值就好了嘛。

　　什么？还是WA？

　　我们来看一看行列式等于0还有什么条件：

　　　　1.有一行或一列全为0的情况；
　　　　2.有两行或两列数值成比例的情况；
　　　　3.行向量之间或列向量之间有相关的情况；
　　　　4.逆矩阵不存在的情况：
　　　　5.行列式对应的矩阵的秩小于行列式的阶数的情况……

　　够了！似乎第二条看起来特别扎眼，于是我们给矩阵里的黑格都随机一个质数权值如何？

　　过了卧槽。

　　二分图匹配：

#include <cstdio>
#include <cstring>
#include <algorithm>
#define MN 205
using namespace std;
bool u[MN],mp[MN][MN];
int mat[][MN];
int t,n;

inline int read()
{
    int n=,f=; char c=getchar();
    while (c<'' || c>'') {if(c=='-')f=-; c=getchar();}
    while (c>='' && c<='') {n=n*+c-''; c=getchar();}
    return n*f;
}

bool dfs(int x)
{
    if (u[x]) return false;
    u[x]=true;
    for (register int i=;i<=n;++i)
    {
        if (!mp[x][i]||mat[][x]==i) continue;
        if (!mat[][i]||dfs(mat[][i])) {mat[][x]=i; mat[][i]=x; return true;}
    }
    return false;
}

int main()
{
    register int i,j;
    t=read();
    while (t--)
    {
        n=read();
        for (i=;i<=n;++i)
            for (j=;j<=n;++j) mp[i][j]=read();
        memset(mat,,sizeof(mat));
        for (i=;i<=n;++i)
        {
            memset(u,,sizeof(u));
            if (!dfs(i)) break;
        }
        if (i<=n) puts("No"); else puts("Yes");
    }
}

　　高斯消元求行列式：

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cstdlib>
#define mod 1000000007
#define MP 2000005
#define MN 205
using namespace std;
int a[MN][MN],p[MP];
bool u[MP];
int t,n,pin;

inline int read()
{
    int n=,f=; char c=getchar();
    while (c<'' || c>'') {if(c=='-')f=-; c=getchar();}
    while (c>='' && c<='') {n=n*+c-''; c=getchar();}
    return n*f;
}

int mi(int x,int y)
{
    register int z=;
    for (;y;x=1LL*x*x%mod,y>>=) if (y&) z=1LL*z*x%mod;
    return z;
}

void init()
{
    register int i,j;
    for (i=;i<MP;++i)
    {
        if (!u[i]) p[++pin]=i;
        for (j=;i*p[j]<MP;++j)
        {
            u[i*p[j]]=true;
            if (i%p[j]==) break;
        }
    }
}

int main()
{
    register int i,j,k,x,mxi,lt;
    srand(); init();
    t=read();
    while (t--)
    {
        n=read();
        for (i=;i<=n;++i)
            for (j=;j<=n;++j)
                if (read()&) a[i][j]=p[(rand()*rand()%pin+rand())%pin+];
                else a[i][j]=;
        for (i=;i<n;++i)
        {
            mxi=i;
            for (j=i+;j<=n;++j) if (a[j][i]>a[mxi][i]) mxi=j;
            if (mxi!=i) swap(a[mxi],a[i]);
            if (!a[i][i]) break;
            for (j=i+;j<=n;++j)
                for (lt=1LL*mi(a[i][i],mod-)*a[j][i]%mod,k=i;k<=n;++k)
                    a[j][k]=(a[j][k]-1LL*a[i][k]*lt%mod+mod)%mod;
        }
        if (i<n||!a[n][n]) puts("No"); else puts("Yes");
    }
}

Last Word

　　行列式还能这么用.jpg。

　　这题又让小C了解了一下行列式的一点点性质，好像还练习了一下乱搞技巧？

　　小C的n^3做法似乎成功拿到了bzoj那一题的垫底：