[BZOJ]1063 道路设计(Noi2008)

　　省选一试后的第一篇blog！

Description

　　Z国坐落于遥远而又神奇的东方半岛上，在小Z的统治时代，公路成为这里主要的交通手段。Z国共有n座城市，一些城市之间由双向的公路所连接。非常神奇的是Z国的每个城市所处的经度都不相同，并且最多只和一个位于它东边的城市直接通过公路相连。Z国的首都是Z国政治经济文化旅游的中心，每天都有成千上万的人从Z国的其他城市涌向首都。为了使Z国的交通更加便利顺畅，小Z决定在Z国的公路系统中确定若干条规划路线，将其中的公路全部改建为铁路。我们定义每条规划路线为一个长度大于1的城市序列，每个城市在该序列中最多出现一次，序列中相邻的城市之间由公路直接相连(待改建为铁路)。并且，每个城市最多只能出现在一条规划路线中，也就是说，任意两条规划路线不能有公共部分。当然在一般情况下是不可能将所有的公路修建为铁路的，因此从有些城市出发去往首都依然需要通过乘坐长途汽车，而长途汽车只往返于公路连接的相邻的城市之间，因此从某个城市出发可能需要不断地换乘长途汽车和火车才能到达首都。我们定义一个城市的“不便利值”为从它出发到首都需要乘坐的长途汽车的次数，而Z国的交通系统的“不便利值”为所有城市的不便利值的最大值，很明显首都的“不便利值”为0。小Z想知道如何确定规划路线修建铁路使得Z国的交通系统的“不便利值”最小，以及有多少种不同的规划路线的选择方案使得“不便利值”达到最小。当然方案总数可能非常大，小Z只关心这个天文数字modQ后的值。注意：规划路线1-2-3和规划路线3-2-1是等价的，即将一条规划路线翻转依然认为是等价的。两个方案不同当且仅当其中一个方案中存在一条规划路线不属于另一个方案。

Input

　　第一行包含三个正整数N、M、Q，其中N表示城市个数,M表示公路总数,N个城市从1~N编号,其中编号为1的是首都。Q表示上文提到的设计路线的方法总数的模数。接下来M行，每行两个不同的正数ai、bi表示有一条公路连接城市ai和城市bi。输入数据保证一条公路只出现一次。

Output

　　包含两行。第一行为一个整数，表示最小的“不便利值”。第二行为一个整数，表示使“不便利值”达到最小时不同的设计路线的方法总数modQ的值。如果某个城市无法到达首都，则输出两行-1。

Sample Input

　　5 4 100
　　1 2
　　4 5
　　1 3
　　4 1

Sample Output

　　1
　　10

HINT

　　对于100%的数据，满足1≤N,M≤100000，1≤Q≤120000000，1≤ai,bi≤N。

Solution

　　题面描述得相当别扭啊，小C也是看过discuss后才知道它给的是一座森林。

　　正常来说学过树链剖分的人只要看到这一条件，题目就已经做完了。

　　题目实际上要我们求的是，求一棵树的树链剖分方案，使得所有点到根的路径上所走的轻边数量的最大值最小。

　　学过树链剖分的人都应该知道，如果按照重链剖分(即重边连向结点更多的子树)来划分一棵树，那么从某个点出发走到根节点最多只要走logN条重链。

　　树剖复杂度的证明在此提一下，其实也很简单，设x个结点组成的树中，所有点到根路径上轻边数量最大值的最大值为f(x)。

　　那么就有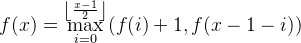，由于f(x)是递增的，所以f(x)必定是从f((x-1)/2)+1转移得到的。

　　所以转移式化简就是：，很显然f(N)是logN级别的。

　　因此答案最大不会超过logN，而且这样形态的树是一棵二叉树。

　　但实际上这道题所说的链剖不是真正意义上的链剖，划分出来的路径是可以拐弯的，因此答案会比logN更小一些，实际上在树的形态是三叉树的情况下答案达到最大，大概是log_3(N)级别。

　　然后知道了以上这些结论我们可以非常容易地写出DP的状态和转移方程：

　　设f[i][j][0/1]表示在结点i的子树中，答案为j，且该子树能否继续向上连边的链剖方案数。转移花log^2随便转移一下就行。

　　最后判断答案的时候简单地根据该处的DP值是否为0来取最小值是不可行的，因为方案数很可能对Q取模等于0，所以这里有一个小技巧，就是方案数为Q的倍数的时候，将对Q取模的值设为Q即可。

　　时间复杂度。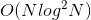

#include <cstdio>
#include <algorithm>
#include <cstring>
#define ll long long
#define MN 100005
#define MS 12
using namespace std;
struct edge{int nex,to;}e[MN<<];
int n,m,mod,pin;
int hr[MN],f[MN][][MS];

inline int read()
{
    int n=,f=; char c=getchar();
    while (c<'' || c>'') {if(c=='-')f=-; c=getchar();}
    while (c>='' && c<='') {n=n*+c-''; c=getchar();}
    return n*f;
}

inline void rw(int& x,int y) {x+=y; if(x>mod)x-=mod;}
inline int modu(ll x) {return !x?:(x-)%mod+;}
inline void ins(int x,int y) {e[++pin]=(edge){hr[x],y}; hr[x]=pin;}

void dfs(int x,int fat)
{
    register int i,j,k;
    int g[][MS],h[][MS+];
    memset(g,,sizeof(g));
    memset(h,,sizeof(h));
    g[][]=;
    for (i=hr[x];i;i=e[i].nex)
    {
        if (e[i].to==fat) continue;
        dfs(e[i].to,x);
        for (j=;j<MS;++j)
            for (k=;k<MS;++k)
            {
                rw(h[][max(j+,k)],modu(1LL*g[][k]*(f[e[i].to][][j]+f[e[i].to][][j])));
                rw(h[][max(j,k)],modu(1LL*g[][k]*f[e[i].to][][j]));
                rw(h[][max(j+,k)],modu(1LL*g[][k]*(f[e[i].to][][j]+f[e[i].to][][j])));
                rw(h[][max(j,k)],modu(1LL*g[][k]*f[e[i].to][][j]));
                rw(h[][max(j+,k)],modu(1LL*g[][k]*(f[e[i].to][][j]+f[e[i].to][][j])));
            }
        for (j=;j<MS;++j)
            g[][j]=h[][j],h[][j]=,
            g[][j]=h[][j],h[][j]=,
            g[][j]=h[][j],h[][j]=;
    }
    for (i=;i<MS;++i)
        f[x][][i]=g[][i],rw(f[x][][i],g[][i]),f[x][][i]=g[][i];
}

int main()
{
    register int i,x,y;
    n=read(); m=read(); mod=read();
    if (m!=n-) return *printf("-1\n-1");
    for (i=;i<=m;++i)
        x=read(),y=read(),
        ins(x,y),ins(y,x);
    dfs(,);
    for (i=;i<MS;++i)
        if (f[][][i]||f[][][i])
            return *printf("%d\n%d",i,(f[][][i]+f[][][i])%mod);
}

Last Word

　　心血来潮写了一下小D的mint，交上去竟然T了，好感度--，表示这模板不是很想再用了。