TopCoder SRM 560 Div 1 - Problem 1000 BoundedOptimization & Codeforces 839 E

传送门：https://284914869.github.io/AEoj/560.html

题目简述：

定义"项"为两个不同变量相乘。 
求一个由多个不同"项"相加，含有n个不同变量的式子的最大值。 
另外限制了每一个变量的最大最小值R[i]和L[i]和所有变量之和的最大值Max。

n<=13

题外话：

刚开始做这道题的时候，感觉意外眼熟？

codeforces 839 E（此题的退化版）:http://codeforces.com/contest/839/problem/E

所以这里将介绍两道题的做法（证明）。

先来看

codeforces 839E

题意：给出一个图的邻接矩阵，要求给每个点赋一个>=0的值，使得点权和为K，并定义每条边权值为两端点点权的乘积，要求最大化边的权值和。

结论：最大化边权就是要将k均分给图中的最大团中的点。

证明：codeforces上给出了一种数学归纳法的证明:http://codeforces.com/blog/entry/53815

但这里将介绍一种新的证明方法：

首先，现在有一种分配点权的方案，

a.对于两个点a,b，假设之间没有边，且与a点相连的点权和为sa，与b点相连的点权和为sb。

再假设当前a的点权为pa，b的点权为pb。

因为全部的点权和=k，所以要维持pa+pb = 一个定值。

这两个点对答案的贡献是pa*sa+pb*sb

若sa>=sb，那么(pa+pb)*sa+0*sb >= pa*sa+pb*sb，对答案的贡献更大。所以把b的点权降为0更优。

若sa<=sb，那么0*sa+(pa+pb)*sb >= pa*sa+pb*sb，对答案的贡献更大。所以把a的点权降为0更优。

由此可见，存在一种最优的分配方案，任意不相连的两个点，其中至少有一个点点权为0。

b.由a得到的结论可得，最优分配方案中，所有点权>0的点之间，两两都有边（即团）。

我们来证明这个团中，每个点的点权相同。

我们先给这个团中的每个点随机赋一个权值（满足权值和=k）。

若在这个团中并不是每个点的点权相同：

假设在这个团中，a,b权值pa不等于pb。（a与b相连）

设与a点相连的点权和（包括pb）为sa = k-pa，与b点相连的点权和（包括pa）为sb = k-pb。

假设把a的点权变为pa+t，b的点权变为pb-t对边的权值和的贡献最大。

这时，边的权值和的变化量为 t*(sa-pb) - t*(sb-pa) + (pa+t)*(pb-t) - pa*pb = - t*t + t*(sa-sb)

那么这变成了一个二次函数最值问题（初中知识吧。。）

t=(sa-sb)/2=(pb-pa)/2的时候最优。

此时a权从pa-->(pa+pb)/2，b权从pb-->(pa+pb)/2。即pa,pb变为了它们的平均数。

所以，可以对这个团进行若干个这样的操作，

每次取两个权值不相同的点，把它们的权值设为它们的平均数。

最终的最优方案，一定是每个点点权相同。

c.接下来我们证明，最大团最优。

若团的大小为s。边的权值和为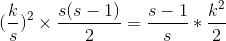

s越大越好。

TopCoder SRM 560 Div 1 - Problem 1000 BoundedOptimization

终于回到正题了。。。

若两个变量的乘积对答案有贡献，就将这两个点之间连一条边。与上题类似，唯一的区别就是：

L[i],R[i],Max的限制。并且，数据范围变小。

其实证明方法类似。

a.存在一种最优的分配方案，任意不相连的两个点，其中至少有一个点点权为为L[i]或R[i]。

证明方法同上。

b.就不一样了

由a得到的结论可得，最优分配方案中，所有点权大于L[i],小于R[i]的点之间，两两都有边（即团）。

这里，设团中的点权和为tot。

设团中某两个点a,b（设点权分别为pa,pb，设pa+pb=S）

设a,b连向团外的点权和分别为Wa,Wb

这两个点对答案的贡献是pa*pb + pa*(tot-S+Wa) + pb*(tot-S+Wb) = -pa^2 + pa*(S+Wa-Wb)  + S*(tot-S+Wb)

又是一个二次函数最值问题。

pa = (S+Wa-Wb)/2，pb = (S+Wb-Wa)/2时

（除非pa或pb不在L到R范围内，此时pa或pb有一项为L或R时更优，则a或b不会在团内，所以不考虑这种情况）

最优。

考虑pa和pb的特点：pa-Wa = (S-Wa-Wb)/2， pb-Wb = (S-Wa-Wb)/2。

于是pa - Wa = pb - Wb

所以这个团中的每一个点，pi - Wi是一个定值。

c.如何求解

一个很简单的思路出来了。

枚举哪些点权为L[i]，哪些点权为R[i]，其余点形成团。

这个枚举的过程是3^n

这个基础上求解，

对于团中的每一个点，可以轻易地求出W[i]（定义见b）

也可以知道团的点权和 <= 一个值。设团的点权和 <= sum

由b的结论可得：团中p[i] - W[i]是一个定值。

设p[i] - W[i] = C

又p[i] = C+W[i] <= R[i]，所以C <= R[i] - W[i]。

p[i] = C+W[i] >= L[i]，所以C >= L[i] - W[i]。

同时sigma{p[i]}<=sum，所以sigma{ C+W[i] }<=R[i]。

由于点权总体越大越好，所以C越大越好。解上述不等式，求出最大的C。

最后求出在这种情况下图的边权和，更新答案，便做完了！

真是道好题！

注：可能我的方法不太优秀，欢迎各位大佬在评论区给出更方便的做法

这里给出代码：

 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;
 #define _CLASSNAME_ BoundedOptimization
 #define _METHODNAME_ maxValue
 #define _RC_ double
 #define _METHODPARMS_ vector <string> s, vector <int> L, vector <int> R, int maxSum
 #define ref(i,x,y)for(int i=x;i<=y;++i)
 #define def(i,x,y)for(int i=x;i>=y;--i)
 double tot, Ans;
 int n, maxsum, w[], W[];
 struct xint { int L, R; }p[];
 bool a[][];
 bool isletter(char c) { return c >= 'a'&&c <= 'z'; }
 double _min(double a, double b) { return a < b ? a : b; }
 void work(int x) {
     if (maxsum < )return;
     if (x == n) {
         double tmp = 2e9; int num = , sum = ;
         ref(i, , n - )if (w[i] < )tmp = _min(tmp, p[i].R - W[i]), ++num, sum += W[i];
         tmp = _min(tmp, 1.0*(maxsum - sum) / num);
         ref(i, , n - )if (w[i] < )if (tmp + W[i] < p[i].L)return;
         double ans = tot, ans2 = (sum + num*tmp)*(sum + num*tmp);
         ref(i, , n - )if (w[i] < )ans += (tmp + W[i])*W[i];
         ref(i, , n - )if (w[i] < )ans2 -= (tmp + W[i])*(tmp + W[i]);
         ans = ans + ans2 / ;
         if (ans > Ans)Ans = ans;
         return;
     }
     int tmp = tot;
     //first case
     w[x] = p[x].L;
     ref(i, , x - )if (w[i] <  && a[x][i])W[i] += w[x];
     ref(i, , x - )if (w[i] >=  && a[x][i])tot += w[i] * w[x];
     maxsum -= w[x]; work(x + ); maxsum += w[x];
     ref(i, , x - )if (w[i] <  && a[x][i])W[i] -= w[x];
     tot = tmp;
     //second case
     w[x] = p[x].R;
     ref(i, , x - )if (w[i] <  && a[x][i])W[i] += w[x];
     ref(i, , x - )if (w[i] >=  && a[x][i])tot += w[i] * w[x];
     maxsum -= w[x]; work(x + ); maxsum += w[x];
     ref(i, , x - )if (w[i] <  && a[x][i])W[i] -= w[x];
     tot = tmp;
     //third case
     w[x] = -; W[x] = ;
     ref(i, , x - )if (w[i] <  && !a[x][i])return;
     ref(i, , x - )if (w[i] >=  && a[x][i])W[x] += w[i];
     work(x + );
     W[x] = ;
 }
 class _CLASSNAME_ {
 public:
     _RC_ _METHODNAME_(_METHODPARMS_)
     {
         string S = "";
         memset(a, , sizeof a);
         memset(W, , sizeof W);
         memset(w, , sizeof w);
         Ans = ; tot = ;
         ref(i, , s.size() - )S = S + s[i];
         ref(i, , S.size() - )if (isletter(S[i]) && isletter(S[i + ]))
             a[S[i] - 'a'][S[i + ] - 'a'] = a[S[i + ] - 'a'][S[i] - 'a'] = ;
         n = L.size();
         ref(i, , n - )p[i].L = L[i], p[i].R = R[i];
         maxsum = maxSum;
         work();
         return _RC_(Ans);
     }
     // BEGIN CUT HERE
 public:
     void run_test(int Case) { if ((Case == -) || (Case == )) test_case_0(); if ((Case == -) || (Case == )) test_case_1(); if ((Case == -) || (Case == )) test_case_2(); if ((Case == -) || (Case == )) test_case_3(); }
 private:
     template <typename T> string print_array(const vector<T> &V) { ostringstream os; os << "{ "; for (typename vector<T>::const_iterator iter = V.begin(); iter != V.end(); ++iter) os << '\"' << *iter << "\","; os << " }"; return os.str(); }
     void verify_case(int Case, const double &Expected, const double &Received) { cerr << "Test Case #" << Case << "..."; if (Expected == Received) cerr << "PASSED" << endl; else { cerr << "FAILED" << endl; cerr << "\tExpected: \"" << Expected << '\"' << endl; cerr << "\tReceived: \"" << Received << '\"' << endl; } }
     void test_case_0() { string Arr0[] = { "ba+cb" }; vector <string> Arg0(Arr0, Arr0 + (sizeof(Arr0) / sizeof(Arr0[]))); int Arr1[] = { ,, }; vector <int> Arg1(Arr1, Arr1 + (sizeof(Arr1) / sizeof(Arr1[]))); int Arr2[] = { ,, }; vector <int> Arg2(Arr2, Arr2 + (sizeof(Arr2) / sizeof(Arr2[]))); int Arg3 = ; double Arg4 = 2.25; verify_case(, Arg4, maxValue(Arg0, Arg1, Arg2, Arg3)); }
     void test_case_1() { string Arr0[] = { "ab" }; vector <string> Arg0(Arr0, Arr0 + (sizeof(Arr0) / sizeof(Arr0[]))); int Arr1[] = { , ,  }; vector <int> Arg1(Arr1, Arr1 + (sizeof(Arr1) / sizeof(Arr1[]))); int Arr2[] = { , ,  }; vector <int> Arg2(Arr2, Arr2 + (sizeof(Arr2) / sizeof(Arr2[]))); int Arg3 = ; double Arg4 = 1.0; verify_case(, Arg4, maxValue(Arg0, Arg1, Arg2, Arg3)); }
     void test_case_2() { string Arr0[] = { "ca+fc+fa+d","b+da+","dc+c","b","+ed+eb+ea" }; vector <string> Arg0(Arr0, Arr0 + (sizeof(Arr0) / sizeof(Arr0[]))); int Arr1[] = { ,,,,, }; vector <int> Arg1(Arr1, Arr1 + (sizeof(Arr1) / sizeof(Arr1[]))); int Arr2[] = { ,,,,, }; vector <int> Arg2(Arr2, Arr2 + (sizeof(Arr2) / sizeof(Arr2[]))); int Arg3 = ; double Arg4 = 2029.25; verify_case(, Arg4, maxValue(Arg0, Arg1, Arg2, Arg3)); }
     void test_case_3() {
         string Arr0[] = { "db+ea+ik+kh+je+","fj+lk+i","d+jb+h","a+gk+mb+ml+lc+mh+cf+fd+","gc+ka+gf+bh+mj+eg+bf+hf+l","b+al+ja+da+i",
             "f+g","h+ia+le+ce+gi+d","h+mc+fe+dm+im+kb+bc+","ib+ma+eb+mf+jk+kc+mg+mk+","gb+dl+ek+hj+dg+hi","+ch+ga+ca+fl+ij+fa+jl+dc+dj+fk","+li+jg" }; vector <string> Arg0(Arr0, Arr0 + (sizeof(Arr0) / sizeof(Arr0[]))); int Arr1[] = { ,,,,,,,,,,,, }; vector <int> Arg1(Arr1, Arr1 + (sizeof(Arr1) / sizeof(Arr1[]))); int Arr2[] = { ,,,,,,,,,,,, }; vector <int> Arg2(Arr2, Arr2 + (sizeof(Arr2) / sizeof(Arr2[]))); int Arg3 = ; double Arg4 = 294978.3333333333; verify_case(, Arg4, maxValue(Arg0, Arg1, Arg2, Arg3));
     }

     // END CUT HERE
 };
 // BEGIN CUT HERE

 int main() {
     _CLASSNAME_ user;
     user.run_test(-);
     getchar();
 }
 // END CUT HERE