Codeforces Round #407 (Div. 1)

人傻不会B 写了C正解结果因为数组开小最后RE了 疯狂掉分

AC:A Rank:392 Rating: 2191-92->2099

A. Functions again

题目大意：给定一个长度为n的数组，求最大的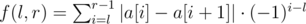，其中1<=l<r<=n。（n<=10^5）

思路：按左端点所在位置的奇偶性分开计算即可。

#include<cstdio>
#include<algorithm>
using namespace std;
#define ll long long
char B[<<],*S=B,C;int X,F;
inline int read()
{
    for(F=;(C=*S++)<''||C>'';)if(C=='-')F=-;
    for(X=C-'';(C=*S++)>=''&&C<='';)X=(X<<)+(X<<)+C-'';
    return X*F;
}
#define MN 200000
int a[MN+];
ll s[MN+];
int main()
{
    fread(B,,<<,stdin);
    int n=read(),i,p;long long mx=,mn;
    for(i=;i<=n;++i)a[i]=read();
    for(mn=,i=p=;i<n;++i,p*=-)
    {
        s[i]=s[i-]+abs(a[i+]-a[i])*p;
        mx=max(mx,s[i]-mn);
        if(~i&)mn=min(mn,s[i]);
    }
    for(mn=,i=,p=-;i<n;++i,p*=-)
    {
        s[i]=s[i-]+abs(a[i+]-a[i])*p;
        mx=max(mx,s[i]-mn);
        if(i&)mn=min(mn,s[i]);
    }
    printf("%I64d",mx);
}

B. Weird journey

题目大意：给定一张n个点m条边的无向图，无重边，有自环，问有多少对边满足有路径有且只经过这两条边一次，且经过其他m-2条边两次。（n,m<=10^6）

思路：分类讨论+大判断。先判连通性，答案为相邻的非自环边对数+自环边数*非自环边数+自环边对数。

#include<cstdio>
char B[<<],*S=B,C;int X;
inline int read()
{
    while((C=*S++)<''||C>'');
    for(X=C-'';(C=*S++)>=''&&C<='';)X=(X<<)+(X<<)+C-'';
    return X;
}
#define MN 1000000
int f[MN+],r[MN+],u[MN+];
int gf(int k){return f[k]?f[k]=gf(f[k]):k;}
int main()
{
    fread(B,,<<,stdin);
    int n,m,x,y,i,cnt=,s=;long long ans=;
    n=read();m=read();
    for(i=;i<=m;++i)
    {
        x=read();y=read();
        if(x==y)++s,u[x]=;
        else ++r[x],++r[y];
        if(gf(x)!=gf(y))++cnt,f[gf(x)]=gf(y);
    }
    for(i=;i<=n;++i)if(!u[i]&&!r[i])++cnt;
    if(cnt<n)return *puts("");
    for(i=;i<=n;++i)ans+=1LL*r[i]*(r[i]-)>>;
    ans+=1LL*s*(m-s)+(1LL*s*(s-)>>);
    printf("%I64d",ans);
}

C. The Great Mixing

题目大意：k种可乐，每种浓度为ai/1000，每种取出任意自然数份混合在一起，问混合出浓度为n/1000的可乐至少要几份。（0<=n,ai<=1000，k<=10^6）

思路：先把所有ai减去n，问题转化为选出的和为0至少选几个，如果都小于0或都大于0则无解，否则容易证明答案至多为O(n)（若ai<0，aj>0，则ai*aj+aj*(-ai)=0），bfs搜出和为x至少要几步，可以很快算出答案。

#include<cstdio>
char B[<<],*S=B,C;int X;
inline int read()
{
    while((C=*S++)<''||C>'');
    for(X=C-'';(C=*S++)>=''&&C<='';)X=(X<<)+(X<<)+C-'';
    return X;
}
#define MN 1000
#define MX 1000000
int u[MN*+],t[MN+],tn,d[MX*+],q[MX*+],qn;
int main()
{
    fread(B,,<<,stdin);
    int n,k,i,j,x,o1=,o2=;
    n=read();k=read();
    for(i=;i<=k;++i)
    {
        if(!(x=read()-n))return *puts("");
        if(x<)o1=;
        if(x>)o2=;
        if(!u[x+MN])u[x+MN]=,t[++tn]=x;
    }
    if(o1||o2)return *puts("-1");
    for(i=;i<=tn;++i)d[q[++qn]=t[i]+MX]=;
    for(i=;i<=qn;++i)
    {
        if(q[i]==MX)return *printf("%d",d[MX]);
        for(j=;j<=tn;++j)
        {
            x=q[i]+t[j];
            if(x<||x>MX*||d[x])continue;
            d[q[++qn]=x]=d[q[i]]+;
        }
    }
}