[Treap][学习笔记]

平衡树

平衡树就是一种可以在log的时间复杂度内完成数据的插入，删除，查找第k大，查询排名，查询前驱后继以及其他许多操作的数据结构。

Treap

treap是一种比较好写，常数比较小，可以实现平衡树基本操作的一种平衡树。treap的平衡是基于随机化。是将堆与二叉查找树结合起来所得到的数据结构。

treap在插入数时，给每个数赋了一个新的随机的值id。在以后的操作中，必须始终使得treap中的id构成一个堆的形态才可以。这样就达到了平衡的目的。

定义

struct node {
   int ch[2],val,id,cnt,siz;
}TR[N];

ch[0/1]分别表示左右儿子。

val是插入的数

id是赋给这个数的一个随机的值

cnt表示这个数字出现的次数

siz为在treap中以这个点为根的数字的个数

更新

void up(int cur) {
   TR[cur].siz = TR[ls].siz + TR[rs].siz + TR[cur].cnt;
}

就是维护一下siz

旋转

f表示将左(0)还是右(1)儿子旋转上来。

如图



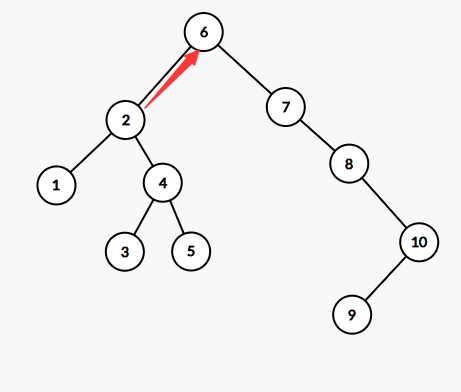
加入我们现在要把2旋转到6这个位置，那么旋转之后6肯定成为了2的右儿子，那4去哪里呢。我们就把4变成6的左儿子，这样就完成了旋转。然后在维护一下siz就行了。

就成了这样



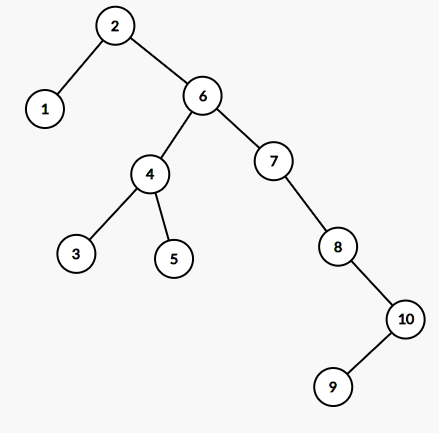
因为treap不存父亲，所以这里要取地址，把6换成2

void rotate(int &cur,int f) {
   int son = TR[cur].ch[f];
   TR[cur].ch[f] = TR[son].ch[f ^ 1];
   TR[son].ch[f ^ 1] = cur;
   up(cur);
   cur = son;
   up(cur);
}

插入

插入一个元素时我们只要按照与二叉查找树相同的方法，找到一个合适的位置插入即可。如果这个元素以前已经插入过了。那么只要把这个数的cnt++就行了。插入完成之后，还要维护id满足堆的形态这个条件。所以如果插入之后的儿子的id比当前节点的id小了，那么就将儿子旋转上来就行了。

void insert(int &cur,int val) {
   if(!cur) {
      cur = ++tot;
      TR[cur].val = val;
      TR[cur].id = rand();
      TR[cur].cnt = TR[cur].siz = 1;
      return;
   }
   TR[cur].siz++;//!!
   if(TR[cur].val == val) { TR[cur].cnt++;return;}
   int d = val > TR[cur].val;
   insert(TR[cur].ch[d],val);
   if(TR[TR[cur].ch[d]].id < TR[cur].id) rotate(cur,d);
}

删除

首先找到要删除的节点，根据这个节点儿子的个数可以分为两种情况。

情况1：这个节点有1个或者0个儿子。那么直接将这个节点变为这个节点的儿子(没有就是0)就行了

情况2：这个节点有2个儿子。那么不断的往下旋转这个节点，知道满足情况1。在旋转的时候应该注意，因为要满足堆这个条件。所以应该将儿子中id较小的那个旋转上来。

void del(int &cur,int val) {
   if(!cur) return;
   if(val == TR[cur].val) {
      if(TR[cur].cnt > 1) {TR[cur].cnt--;TR[cur].siz--; return;}
      if(!ls || !rs) {cur = ls + rs;return;}
      int d = TR[rs].id < TR[ls].id;
      rotate(cur,d);
      del(cur,val);
   }
   else TR[cur].siz--,del(TR[cur].ch[val > TR[cur].val],val);
}

查找排名

这个就真的和二叉搜索树一样了。如果要找的那个数字比当前节点大。那么就将排名加上左子树大小，然后搜右子树，否则搜左子树。

int Rank(int cur,int val) {
   if(!cur) return 0;
   if(val == TR[cur].val) return TR[ls].siz + 1;
   if(val < TR[cur].val) return Rank(ls,val);
   return Rank(rs,val) + TR[ls].siz + TR[cur].cnt;
}

查找第k大(排名为k的元素)

和查找排名差不多。只要不断的记录下要查找当前子树中的第几大。如果比左子树大小加上根节点大小还大，那么就减去左子树大小和根大小，并查找右子树，否则查找左子树

int kth(int cur,int now) {
   while(1) {
      if(TR[ls].siz >= now) cur = ls;
      else if(TR[ls].siz + TR[cur].cnt < now) now -=TR[ls].siz + TR[cur].cnt,cur = rs;
      else return TR[cur].val;
   }
}

前驱

还是从根往下搜索，如果要找的数比当前根节点要大，那么就搜索右子树，并将搜到的答案与当前根取max，否则就搜索左子树

int pred(int cur,int val) {
   if(!cur) return -INF;
   if(val <= TR[cur].val) return pred(ls,val);//!!!
   return max(pred(rs,val),TR[cur].val);
}

后继

跟前驱同理

int nex(int cur,int val) {
   if(!cur) return INF;
   if(val >= TR[cur].val) return nex(rs,val);//!!!
   return min(nex(ls,val),TR[cur].val);
}

一言

迷途经累劫，悟则刹那间。 ——六祖坛经