字符串匹配算法-kmp算法

一原理：

部分转自：http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html

字符串匹配是计算机的基本任务之一。

举例来说，有一个字符串"BBC ABCDAB ABCDABCDABDE"，我想知道，里面是否包含另一个字符串"ABCDABD"？

许多算法可以完成这个任务，Knuth-Morris-Pratt算法（简称KMP）是最常用的之一。它以三个发明者命名，起头的那个K就是著名科学家Donald Knuth。

这种算法不太容易理解，网上有很多解释，但读起来都很费劲。直到读到Jake Boxer的文章，我才真正理解这种算法。下面，我用自己的语言，试图写一篇比较好懂的KMP算法解释。

1.

首先，字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符，进行比较。因为B与A不匹配，所以搜索词后移一位。

2.

因为B与A不匹配，搜索词再往后移。

3.

就这样，直到字符串有一个字符，与搜索词的第一个字符相同为止。

4.

接着比较字符串和搜索词的下一个字符，还是相同。

5.

直到字符串有一个字符，与搜索词对应的字符不相同为止。

6.

这时，最自然的反应是，将搜索词整个后移一位，再从头逐个比较。这样做虽然可行，但是效率很差，因为你要把"搜索位置"移到已经比较过的位置，重比一遍。

7.

一个基本事实是，当空格与D不匹配时，你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是，设法利用这个已知信息，不要把"搜索位置"移回已经比较过的位置，继续把它向后移，这样就提高了效率。

8.

怎么做到这一点呢？可以针对搜索词，算出一张《部分匹配表》（Partial Match Table）。这张表是如何产生的，后面再介绍，这里只要会用就可以了。

9.

已知空格与D不匹配时，前面六个字符"ABCDAB"是匹配的。查表可知，最后一个匹配字符B对应的"部分匹配值"为2，因此按照下面的公式算出向后移动的位数：

　　移动位数 = 已匹配的字符数 - 对应的部分匹配值

因为 6 - 2 等于4，所以将搜索词向后移动4位。

10.

因为空格与Ｃ不匹配，搜索词还要继续往后移。这时，已匹配的字符数为2（"AB"），对应的"部分匹配值"为0。所以，移动位数 = 2 - 0，结果为 2，于是将搜索词向后移2位。

11.

因为空格与A不匹配，继续后移一位。

12.

逐位比较，直到发现C与D不匹配。于是，移动位数 = 6 - 2，继续将搜索词向后移动4位。

13.

逐位比较，直到搜索词的最后一位，发现完全匹配，于是搜索完成。如果还要继续搜索（即找出全部匹配），移动位数 = 7 - 0，再将搜索词向后移动7位，这里就不再重复了。

14.

下面介绍《部分匹配表》是如何产生的。

首先，要了解两个概念："前缀"和"后缀"。 "前缀"指除了最后一个字符以外，一个字符串的全部头部组合；"后缀"指除了第一个字符以外，一个字符串的全部尾部组合。

15.

"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例，

　　－　"A"的前缀和后缀都为空集，共有元素的长度为0；

　　－　"AB"的前缀为[A]，后缀为[B]，共有元素的长度为0；

　　－　"ABC"的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；

　　－　"ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；

　　－　"ABCDA"的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为"A"，长度为1；

　　－　"ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为"AB"，长度为2；

　　－　"ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。

16.

"部分匹配"的实质是，有时候，字符串头部和尾部会有重复。比如，"ABCDAB"之中有两个"AB"，那么它的"部分匹配值"就是2（"AB"的长度）。搜索词移动的时候，第一个"AB"向后移动4位（字符串长度-部分匹配值），就可以来到第二个"AB"的位置。

二：next数组详解

public static int[] makeNext(String str) {
        char[] strCharArr = str.toCharArray();
        int[] next = new int[strCharArr.length];
        next[0] = 0; // 模版字符串的第一个字符的最大前后缀长度为0
        // for循环，从第二个字符开始，依次计算每一个字符对应的next值
        for (int i = 1, k = 0; i < strCharArr.length; i++) {// q:模版字符串下标；k:最大前后缀长度
            while (k > 0 && strCharArr[k] != strCharArr[i]) {// 递归的求出P[0]···P[q]的最大的相同的前后缀长度k
                k = next[k - 1];
            }
            if (strCharArr[i] == strCharArr[k]) {// 如果相等，那么最大相同前后缀长度加1
                k++;
            }
            next[i] = k;
        }
        return next;
    }

　　

现在我着重讲解一下while循环所做的工作：

1. 　　已知前一步计算时最大相同的前后缀长度为k（k>0），即P[0]···P[k-1]；
2. 　　此时比较第k项P[k]与P[q],如图1所示
3. 　　如果P[K]等于P[q]，那么很简单跳出while循环;
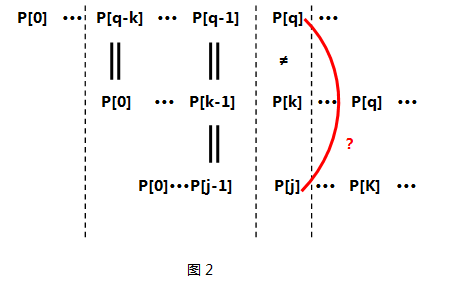
4. 　　那么我们应该利用已经得到的next[0]···next[k-1]来求P[0]···P[k-1]这个子串中最大相同前后缀，可能有同学要问了——为什么要求P[0]···P[k-1]的最大相同前后缀呢？？？是啊！为什么呢？ 原因在于P[k]已经和P[q]失配了，而且P[q-k] ··· P[q-1]又与P[0] ···P[k-1]相同，看来P[0]···P[k-1]这么长的子串是用不了了，那么我要找个同样也是P[0]打头、P[k-1]结尾的子串即P[0]···P[j-1](j==next[k-1])，看看它的下一项P[j]是否能和P[q]匹配。如图2所示

全部代码：

/**
 * code by me
 * <p>
 * Data:2017/8/21 Time:10:43
 * User:lbh
 */
public class KMP {

    public static int[] makeNext(String str) {
        char[] strCharArr = str.toCharArray();
        int[] next = new int[strCharArr.length];
        next[0] = 0; // 模版字符串的第一个字符的最大前后缀长度为0
        // for循环，从第二个字符开始，依次计算每一个字符对应的next值
        for (int i = 1, k = 0; i < strCharArr.length; i++) {// q:模版字符串下标；k:最大前后缀长度
            while (k > 0 && strCharArr[k] != strCharArr[i]) {// 递归的求出P[0]···P[q]的最大的相同的前后缀长度k
                k = next[k - 1];
            }
            if (strCharArr[i] == strCharArr[k]) {// 如果相等，那么最大相同前后缀长度加1
                k++;
            }
            next[i] = k;
        }
        return next;
    }

    public static int kmp(String text, String target) {
        if (target == null || "".equals(target) || text == null || "".equals(text)) {
            return 0;
        }
        int[] next = makeNext(target);
        char[] textCharArr = text.toCharArray();
        char[] targetCharArr = target.toCharArray();
        int targetLen = targetCharArr.length;
        for (int i = 0, k = 0; i < textCharArr.length; i++) {
            while (k > 0 && targetCharArr[k] != textCharArr[i]) {
                k = next[k - 1];
            }
            if (targetCharArr[k] == textCharArr[i]) {
                k++;
            }
            if (k == targetLen) {
                return i - targetLen + 1;
            }
        }
        return 0;
    }

    public static void main(String[] args) {
        System.out.println(Arrays.toString(makeNext("你好，我是刘宝华，你好，请问有什么事情吗？")));
        String text = "今天星期一，你好，我是刘宝华，你好，请问有什么事情吗？O(∩_∩)O";
        String target = "你好，我是刘宝华，你好，请问有什么事情吗？";
        System.out.println(kmp(text,target));
    }
}