机器学习理论基础学习4--- SVM（基于结构风险最小化）

一、什么是SVM？

　　SVM（Support Vector Machine）又称为支持向量机，是一种二分类的模型。当然如果进行修改之后也是可以用于多类别问题的分类。支持向量机可以分为线性和非线性两大类。其主要思想为找到空间中的一个更够将所有数据样本划开的超平面，并且使得本集中所有数据到这个超平面的距离最短。

　　那么，又怎么表示这个“都正确”呢？可以这样考虑：就是让那些“很有可能不正确”的数据点彼此分开得明显一点就可以了。对于其它“不那么可能不正确”或者说“一看就很正确”的数据点，就可以不用管了。这也是SVM名称的由来，模型是由那些支持向量（Support Vector）决定的。这也是为什么SVM对outlier不敏感。SVM 的最终决策函数只由少数的支持向量所确定,计算的复杂性取决于支持向量的数目,而不是样本空间的维数,这在某种意义上避免了“维数灾难”。

---

二、有几种SVM？

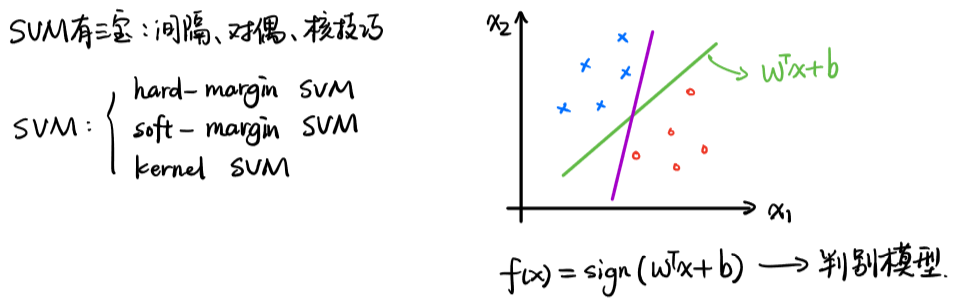
硬间隔SVM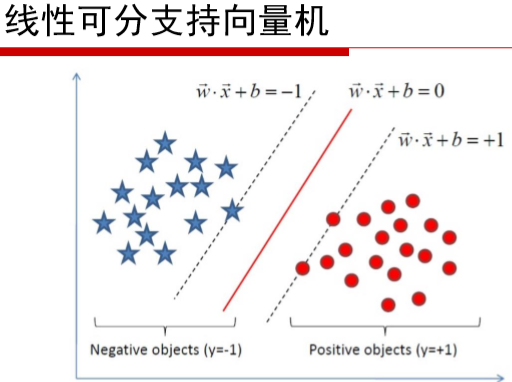
软间隔SVM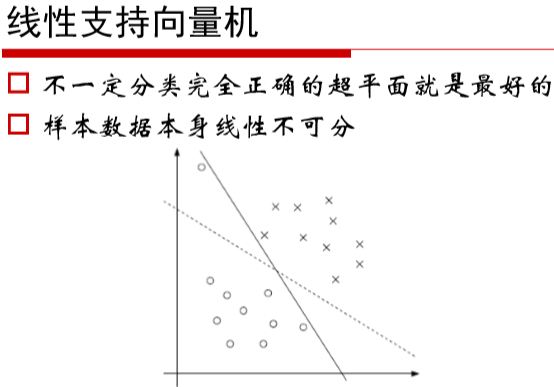
kernel SVM

---

三、几何形式>>>>>>最大间隔分类器的数学形式

---

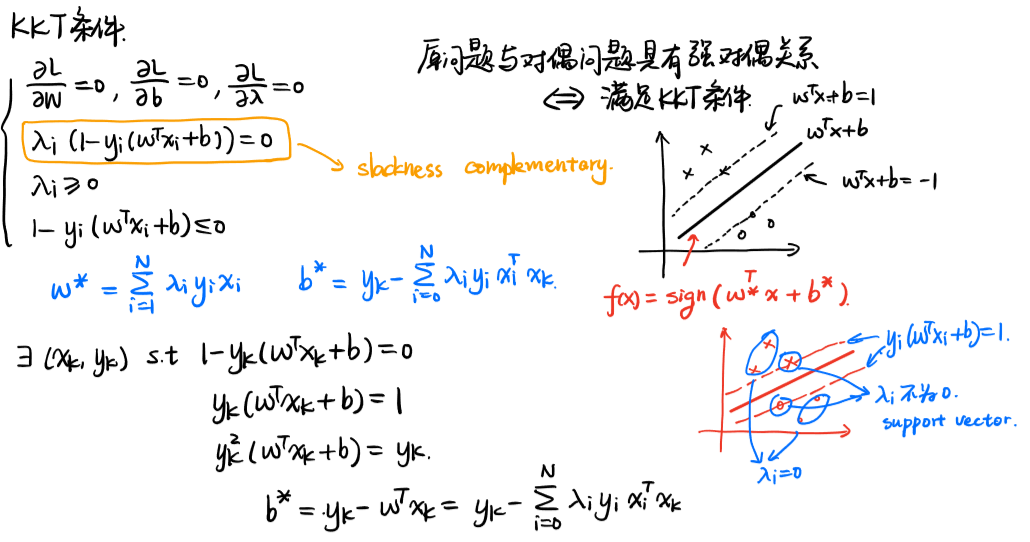
四、硬间隔SVM的推导

利用拉格朗日函数将带约束的原问题转换为无约束的问题，再利用强对偶性，得到无约束问题的等价形式，从而得到硬间隔SVM的数学形式

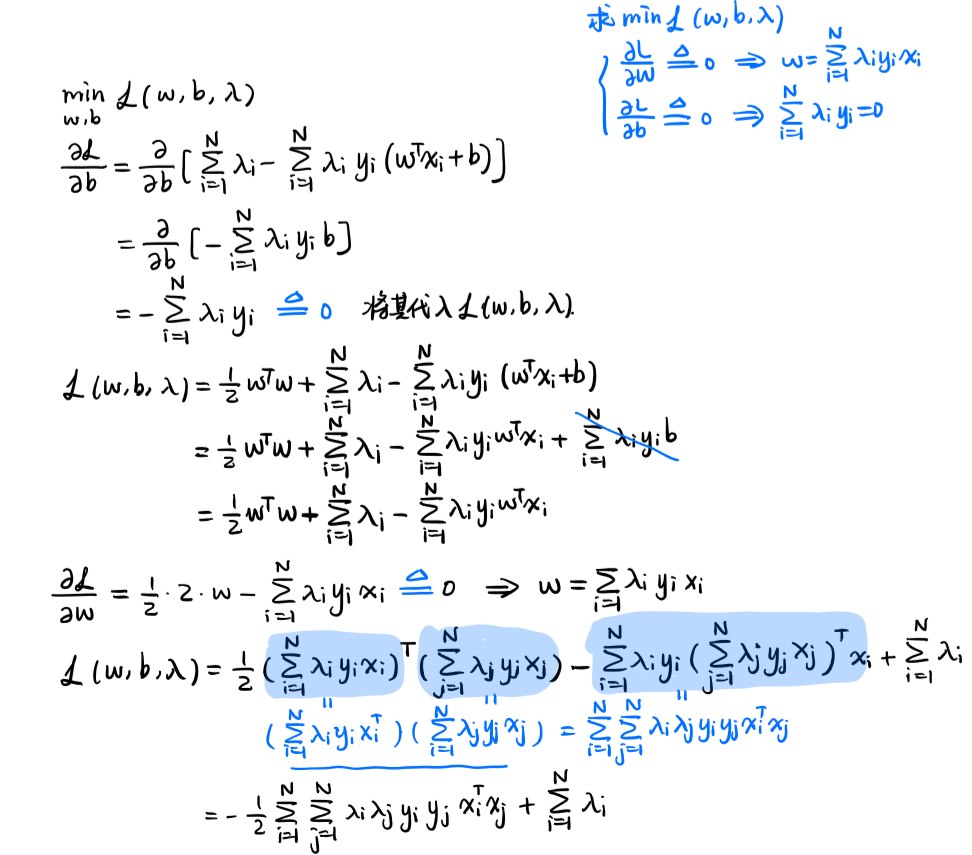
为什么将原问题转为对偶问题？

• 对偶问题将原始问题中的约束转为了对偶问题中的等式约束（KKT）
• 方便核函数的引入
• 改变了问题的复杂度。由求特征向量w转化为求比例系数a，在原始问题下，求解的复杂度与样本的维度有关，即w的维度。在对偶问题下，只与样本数量有关。

---

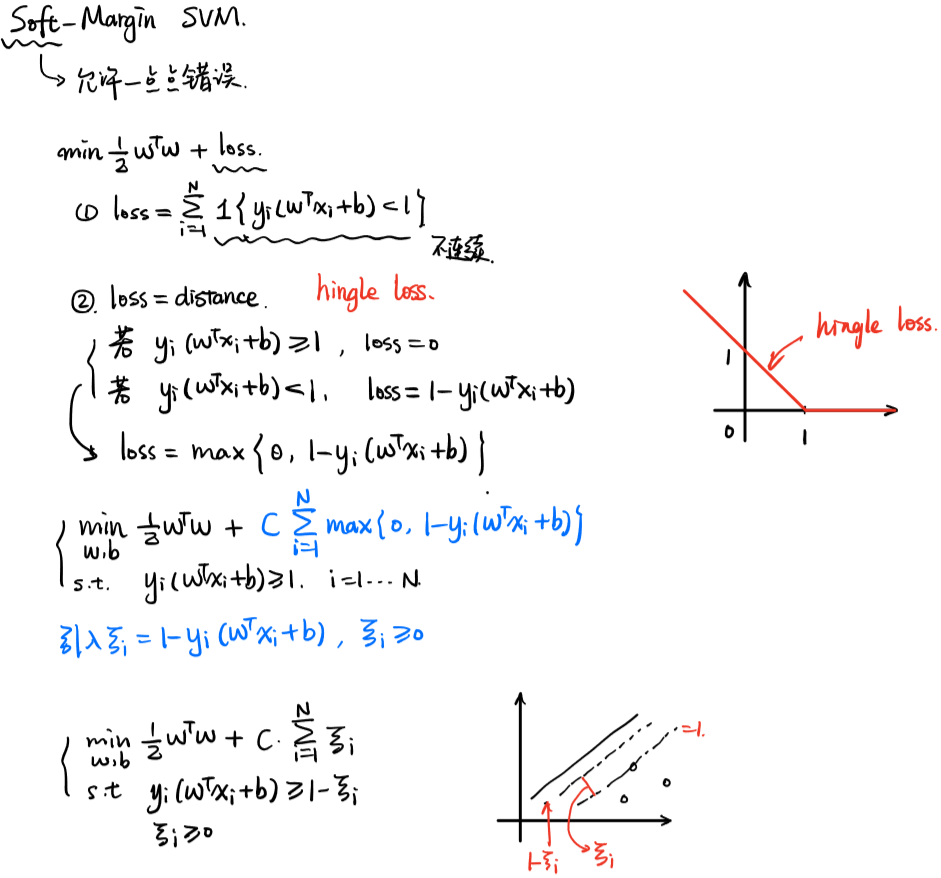
五、软间隔SVM的推导

---

六、核函数的选择

1、线性核函数

　　
线性核，主要用于线性可分的情况，我们可以看到特征空间到输入空间的维度是一样的，其参数少速度快，对于线性可分数据，其分类效果很理想，因此我们通常首先尝试用线性核函数来做分类，看看效果如何，如果不行再换别的

2、多项式核函数

　　
多项式核函数可以实现将低维的输入空间映射到高纬的特征空间，但是多项式核函数的参数多，当多项式的阶数比较高的时候，核矩阵的元素值将趋于无穷大或者无穷小，计算复杂度会大到无法计算。

3、高斯（RBF）核函数

　　 

高斯径向基函数是一种局部性强的核函数，其可以将一个样本映射到一个更高维的空间内，该核函数是应用最广的一个，无论大样本还是小样本都有比较好的性能，而且其相对于多项式核函数参数要少，因此大多数情况下在不知道用什么核函数的时候，优先使用高斯核函数。

4、sigmoid核函数

　　  

采用sigmoid核函数，支持向量机实现的就是一种多层神经网络。

因此，在选用核函数的时候，如果我们对我们的数据有一定的先验知识，就利用先验来选择符合数据分布的核函数；如果不知道的话，通常使用交叉验证的方法，来试用不同的核函数，误差最小的即为效果最好的核函数，或者也可以将多个核函数结合起来，形成混合核函数。选择核函数的技巧：

• 如果特征的数量大到和样本数量差不多，则选用LR或者线性核的SVM；
• 如果特征的数量小，样本的数量正常，则选用SVM+高斯核函数；
• 如果特征的数量小，而样本的数量很大，则需要手工添加一些特征从而变成第一种情况。

---

七、SVM总结

SVM算法是一个很优秀的算法，在集成学习和神经网络之类的算法没有表现出优越性能之前，SVM算法基本占据了分类模型的统治地位。目前在大数据时代的大样本背景下，SVM由于其在大样本时超级大的计算量，热度有所下降，但仍然是一个常用的机器学习算法。

SVM的特点有：

• 非线性映射是SVM方法的理论基础,SVM利用内积核函数代替向高维空间的非线性映射；
• 对特征空间划分的最优超平面是SVM的目标,最大化分类边际的思想是SVM方法的核心；
• 支持向量是SVM的训练结果,在SVM分类决策中起决定作用的是支持向量。
• SVM 是一种有坚实理论基础的新颖的小样本学习方法。它基本上不涉及概率测度及大数定律等,因此不同于现有的统计方法。从本质上看,它避开了从归纳到演绎的传统过程,实现了高效的从训练样本到预报样本的“转导推理”,大大简化了通常的分类和回归等问题。
• SVM 的最终决策函数只由少数的支持向量所确定,计算的复杂性取决于支持向量的数目,而不是样本空间的维数,这在某种意义上避免了“维数灾难”。
• 少数支持向量决定了最终结果,这不但可以帮助我们抓住关键样本、“剔除”大量冗余样本,而且注定了该方法不但算法简单,而且具有较好的“鲁棒”性。这种“鲁棒”性主要体现在:

①增、删非支持向量样本对模型没有影响;

②支持向量样本集具有一定的鲁棒性;

③有些成功的应用中,SVM 方法对核的选取不敏感

• SVM学习问题可以表示为凸优化问题，因此可以利用已知的有效算法发现目标函数的全局最小值。而其他分类方法（如基于规则的分类器和人工神经网络）都采用一种基于贪心学习的策略来搜索假设空间，这种方法一般只能获得局部最优解。
• SVM通过最大化决策边界的边缘来控制模型的能力。尽管如此，用户必须提供其他参数，如使用核函数类型和引入松弛变量等。
• SVM在小样本训练集上能够得到比其它算法好很多的结果。支持向量机之所以成为目前最常用，效果最好的分类器之一，在于其优秀的泛化能力，这是是因为其本身的优化目标是结构化风险最小，而不是经验风险最小，因此，通过margin的概念，得到对数据分布的结构化描述，因此减低了对数据规模和数据分布的要求。SVM也并不是在任何场景都比其他算法好，对于每种应用，最好尝试多种算法，然后评估结果。如SVM在邮件分类上，还不如逻辑回归、KNN、bayes的效果好。
• 它基于结构风险最小化原则，这样就避免了过学习问题，泛化能力强。
• 它是一个凸优化问题，因此局部最优解一定是全局最优解的优点。
• 泛华错误率低，分类速度快，结果易解释

SVM算法的主要优点有：

  1) 解决高维特征的分类问题和回归问题很有效，在特征维度大于样本数时依然有很好的效果。

  2) 仅仅使用一部分支持向量来做超平面的决策，无需依赖全部数据。

  3) 有大量的核函数可以使用，从而可以很灵活的来解决各种非线性的分类回归问题。

  4) 样本量不是海量数据的时候，分类准确率高，泛化能力强。

 

SVM算法的主要缺点有：

  1) 如果特征维度远远大于样本数，则SVM表现一般。

  2) SVM在样本量非常大，核函数映射维度非常高时，计算量过大，不太适合使用。

  3) 非线性问题的核函数的选择没有通用标准，难以选择一个合适的核函数。

  4) SVM对缺失数据敏感。

---

补充：约束优化问题和对偶问题

---

参考文献：

【1】【机器学习】支持向量机SVM原理及推导

【2】机器学习之软间隔支持向量机（机器学习技法）