C# 高性能的数组 高性能数组队列实战 HslCommunication的SharpList类详解

本文将使用一个gitHub开源的组件技术来实现这个功能

github地址：https://github.com/dathlin/HslCommunication                             如果喜欢可以star或是fork，还可以打赏支持。

官网地址：http://www.hslcommunication.cn/         打赏请认准官网

场景需求

---

我们会有对缓存数据的需求。C#本身提供了固定长度的数组 T[]  , 可变长度的List<T>  当然还有先入先出，后入后出的队列。

通常实际中，我们需要维护一个缓存的数组队列，比如一个int数组，长度为1000个，当我们读取到数据后，需要往里面添加数据，然后所有的数据都是往左挪动。最后这个数据是线程安全的操作。

第一种写法，就是循环挪动数据：

int[] buffer = new int[1000];

                hybirdLock.Enter( );

                for (int j = 0; j < buffer.Length - 1; j++)
                {
                    buffer[j] = buffer[j + 1];
                }

                buffer[999] = 100;

                hybirdLock.Leave( );

第二种写法，批量挪动数据

int[] buffer = new int[1000];

                hybirdLock.Enter( );

                int[] newbuffer = new int[1000];
                Array.Copy( buffer, 0, newbuffer, 0, 999 );
                newbuffer[999] = 100;
                buffer = newbuffer;

                hybirdLock.Leave( );

　　

第三种写法，就是List泛型类，和先入先出的用法差不多

int[] buffer = new int[1000];
List<int> list = new List<int>( buffer );

 hybirdLock.Enter( );

                list.Add( 100 );
                list.RemoveAt( 0 );

                hybirdLock.Leave( );

　　

第四种写法：SharpList<T> 类型实现

            SharpList<int> sharpList = new SharpList<int>( 1000, true );
            sharpList.Add( 1000 );

初步对比，SharpList代码上更加精简。因为内置了线程安全，自动挪动数据。

上述代码我们定义了一个长度为1000的int类型的数组对象。实例化之后，其本身就是一个1000个长度的 int[] 数组，当 Add(100);时，最右侧就多了一个100的数据。

SharpList<T> 提供了几个方法来方便快捷的操作数据。比如根据索引为访问：

int value = sharpList[0];  // 得到0
int value2 = sharpList[999]; // 得到100

int[] tmp = sharpList.ToArray();        // 得到数组数据的副本。[0,,,,,,,,,,999]

　　

当新增数据的时候，也支持批量的新增。

性能对比

---

我们将上述的四种方式各自运行100W次，查看下各自的性能差异，具体运行时间取决于cpu型号，内存，等因数，此处仅仅是一个参考。

            SimpleHybirdLock hybirdLock = new SimpleHybirdLock( );

            int[] buffer = new int[1000];
            DateTime start = DateTime.Now;
            for (int i = 0; i < 1000000; i++)
            {
                hybirdLock.Enter( );

                for (int j = 0; j < buffer.Length - 1; j++)
                {
                    buffer[j] = buffer[j + 1];
                }

                buffer[999] = i;

                hybirdLock.Leave( );
            }

            Console.WriteLine( (DateTime.Now - start).TotalMilliseconds );

            start = DateTime.Now;
            for (int i = 0; i < 1000000; i++)
            {
                hybirdLock.Enter( );

                int[] newbuffer = new int[1000];
                Array.Copy( buffer, 0, newbuffer, 0, 999 );
                newbuffer[999] = i;
                buffer = newbuffer;

                hybirdLock.Leave( );
            }

            Console.WriteLine( (DateTime.Now - start).TotalMilliseconds );

            List<int> list = new List<int>( buffer );
            start = DateTime.Now;
            for (int i = 0; i < 1000000; i++)
            {
                hybirdLock.Enter( );

                list.Add( i );
                list.RemoveAt( 0 );

                hybirdLock.Leave( );
            }

            Console.WriteLine( (DateTime.Now - start).TotalMilliseconds );

            SharpList<int> sharpList = new SharpList<int>( 1000, true );
            start = DateTime.Now;
            for (int i = 0; i < 1000000; i++)
            {
                sharpList.Add( i );
            }
            Console.WriteLine( (DateTime.Now - start).TotalMilliseconds );

            int[] data = sharpList.ToArray( );

            Console.ReadLine( );

　　

我们跑三次，对比结果。

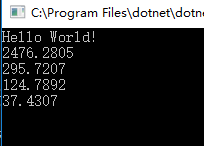
我们看到SharpList<T> 类仅仅消耗了37ms，完成了100W次数据的新增和挪动。

为什么会有那么大的性能差异呢？就要深入源代码查看了。

深度剖析

---

超高的性能的本质在于减少大块的数据移动，先内部实例化一个远比需求还大的多的数据对象

array = new T[capacity + count];

　　

当有数据新增进来的时候，实际不需要移动

        /// <summary>
        /// 新增一个数据值
        /// </summary>
        /// <param name="value">数据值</param>
        public void Add( T value )
        {
            hybirdLock.Enter( );

            if(lastIndex < (capacity + count))
            {
                array[lastIndex++] = value;
            }
            else
            {
                // 需要重新挪位置了
                T[] buffer = new T[capacity + count];
                Array.Copy( array, capacity, buffer, 0, count );
                array = buffer;
                lastIndex = count;
            }

            hybirdLock.Leave( );
        }

　　先进行自然的赋值，这时的性能就非常快了，然后提高游标的索引。当缓存都不够时，再去复制挪动一次数据。

当然，当要获取数据时，就需要进行根据当前的活动游标进行获取到正确的数据。

        /// <summary>
        /// 获取数据的数组值
        /// </summary>
        /// <returns>数组值</returns>
        public T[] ToArray( )
        {
            T[] result = null;
            hybirdLock.Enter( );

            if (lastIndex < count)
            {
                result = new T[lastIndex];
                Array.Copy( array, 0, result, 0, lastIndex );
            }
            else
            {
                result = new T[count];
                Array.Copy( array, lastIndex - count, result, 0, count );
            }
            hybirdLock.Leave( );
            return result;
        }

　　

相关的话题，后续补充。