利用MATLAB进行曲线拟合

软件环境：MATLAB2013a

一、多项式拟合

多项式拟合是利用多项式最佳地拟合观测数据，使得在观测数据点处的误差平方和最小。

在MATLAB中，利用函数ployfit和ployval进行多项式拟合。

函数ployfit根据观测数据及用户指定的多项式阶数得到光滑曲线的多项式表示，polyfit的一般调用格式为：P = polyfit(x,y,n)。其中x为自变量，y为因变量，n为多项式阶数。

polyval的输入可以是标量或矩阵，调用格式为

pv = polyval(p,a)
pv = polyval(p,A)

其中，p为多项式表示，a为标量，A为矩阵。当输入参数为M*N矩阵A时，函数返回值pv也是M*N矩阵，且pv(i,j) = polyval(p,A(i,j))。

1，多项式拟合示例：对ln(1+x)在[0,1]的采样数据作多项式拟合

（1）对ln(1+x)在[0,1]内采样得到观测数据x、y。

>> x = :0.1:1.0;

>> y = log(+x);

（2）调用函数polyfit对观测数据x、y作三阶多项式拟合。

>> P = polyfit(x,y,)

运行结果如下：

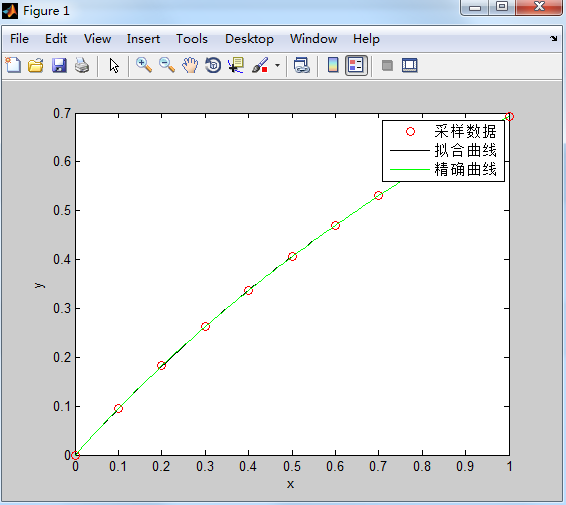
P对应的多项式为0.1079 - 0.3974x + 0.9825x²+ 0.004x³.

（3）分别作拟合曲线和理论曲线

>> xi = :0.01:1.0;

>> yi = polyval(P,xi);   %多项式求值

>> plot(x,y,'ro');         %观测数据点

>> hold on;

>> plot(xi,yi,'k');         %作拟合曲线

>> plot(xi,log(+xi),'g');    %理论曲线

>> xlabel('x');

>> ylabel('y');

>> legend('采样数据','拟合曲线','精确曲线');

效果如下：

二、指数函数拟合

1，指数函数拟合示例：对 1 - √x 在[0,1]的采样数据作指数函数拟合。

（1）对 1 - √x 在[0,1]内采样得到观测数据 x、y。

>> x = :0.01:0.99;

>> y =  - sqrt(x);

（2）调用函数polyfit对 x 、lny 作一阶多项式拟合。

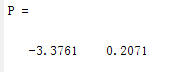
>> P = polyfit(x,log(y),)

运行结果如下：

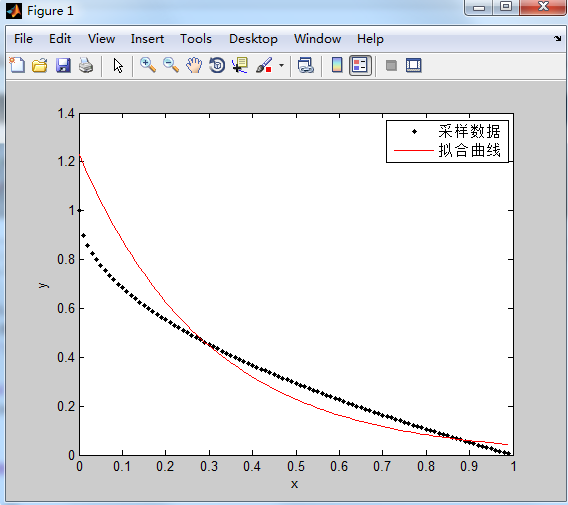
（3）求得拟合曲线。

>> yi = exp(polyval(P,x));

（4）分别作观测数据点、拟合曲线和理论曲线。

>> yi = exp(polyval(P,x));

>> plot(x,y,'k.');

>> hold on;

>> plot(x,yi,'r');

>> xlabel('x');

>> ylabel('y');

>> legend('采样数据','拟合曲线');

>> hold off;

运行结果如下：

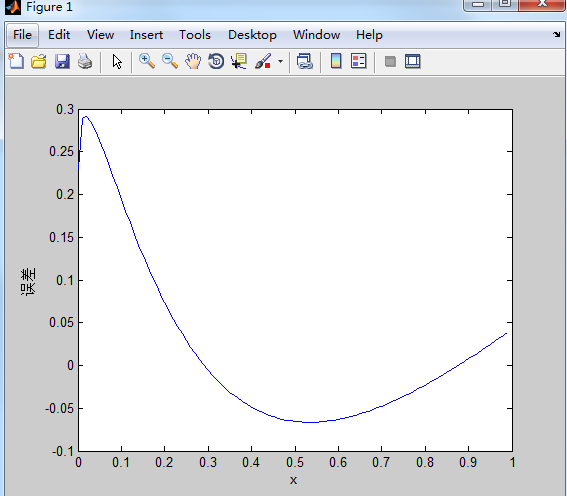
（5）分析拟合误差。

>> e = yi - y;

>> plot(x,e);

>> xlabel('x');

>> ylabel('误差');

运行结果如下：

三、交互式曲线拟合工具

MATLAB为用户提供了一个交互式曲线拟合工具 Basic Fitting interface。通过该工具，我们无须编写代码就可以完成一些常用的曲线拟合。

（1）载入census data数据。

>> load census

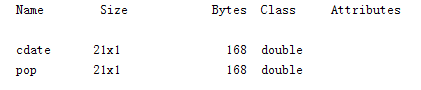
此时MATLAB基本工作空间生成两个double型列向量 cdate 和 pop，cdate 表示1790~1990内10年为间隔的年份，pop为对应年份美国的人口。

>> whos

运行结果如下：

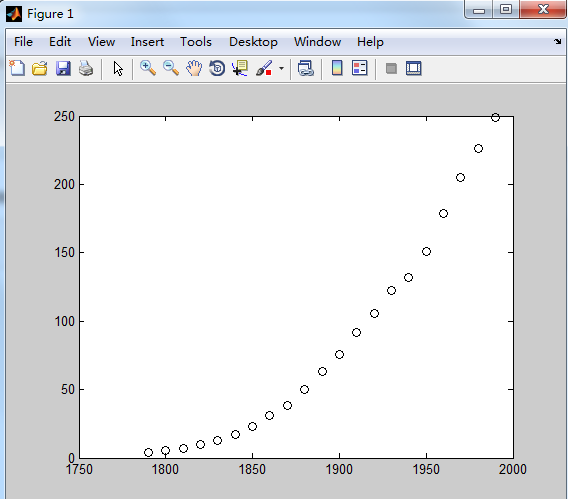
（2）作census data点图。

>> plot(cdate,pop,'ko');

运行结果如下：

（3）在MATLAB的figure中选择Tool → Basic Fitting，即得到Basic Fitting interface 界面。

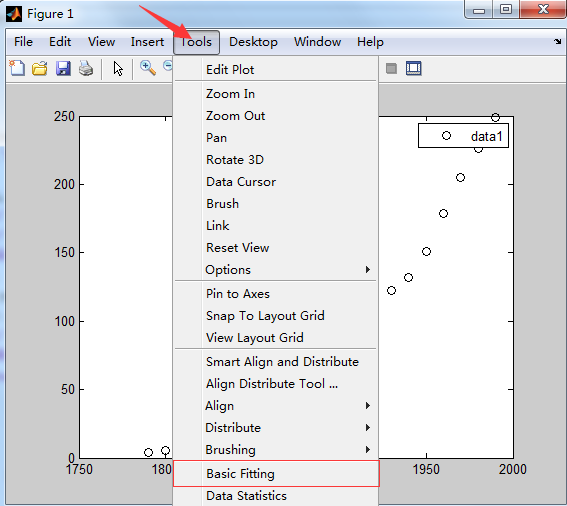
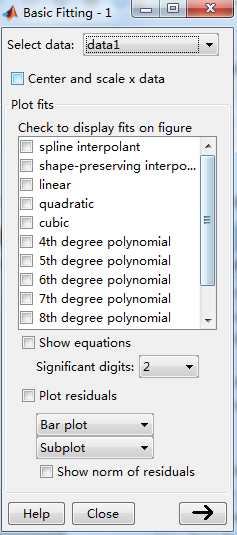
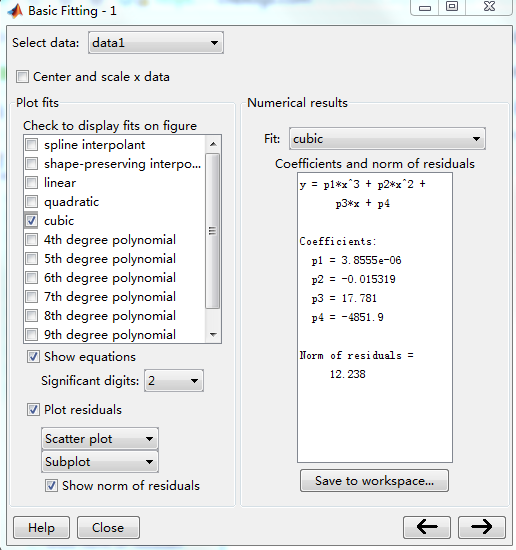
用户通过Plot fits面板选择不同的曲线拟合方式，为了便于比较，我们可以选择多种拟合方式，从而选择效果最好的一种拟合。

如果某次拟合的效果较差，MATLAB会给出警告，这时用户可以试着通过 Center and Scale X data 改善拟合效果。

如果Show equations复选框被选中，那么图形窗口会显示拟合方程；如果Plot residuals复选框被选中，那么拟合效果将显示误差余量。此外，还可以选择不同的显示类型，如Bar Plot（直方图）、Scatter Plot（散点图）、Line Plot（线图）。

如果Show norm of residuals复选框被选中，那么误差余量图将显示误差余量的范数。

单击，得到如下界面，通过该界面我们能看到拟合的数值结果：

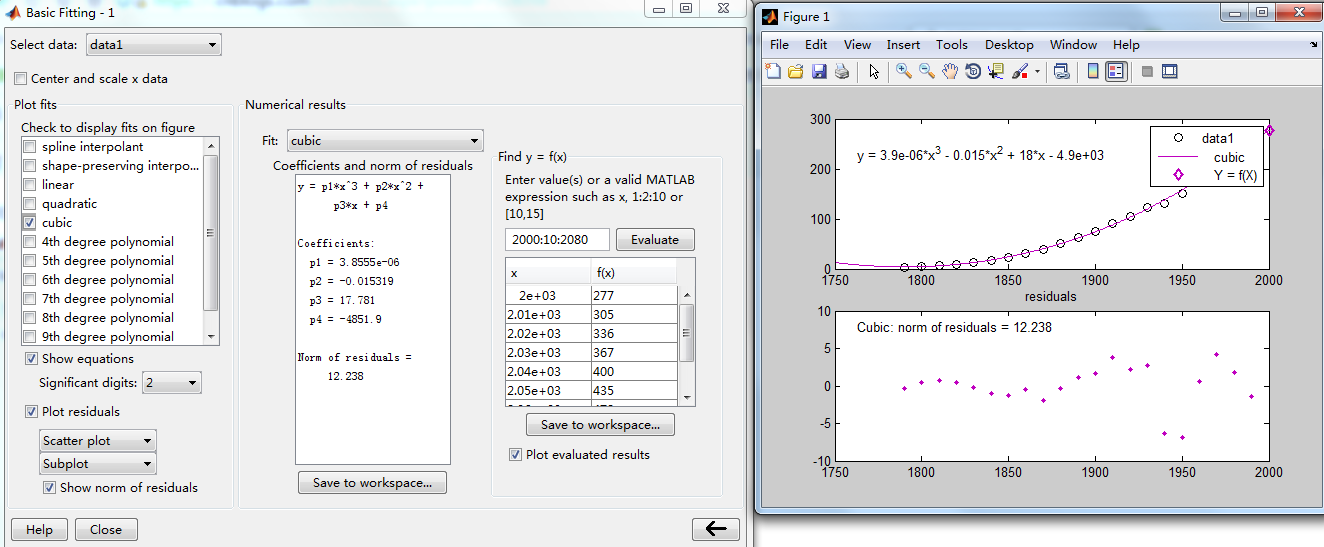
再次单击，得到如下界面。通过该界面右侧的面板，我们可以得到任意点处拟合函数的值，如在编辑框中输入 2000：10：2080，并单击Evaluate按钮，计算结果将显示在列表框中。如果Plot evaluated result复选框被选中，那么计算结果将显示在拟合曲线中。