Multinoulli distribution

https://www.statlect.com/probability-distributions/multinoulli-distribution3

Multinoulli distribution

The Multinoulli distribution (sometimes also called categorical distribution) is a generalization of the Bernoulli distribution. If you perform an experiment that can have only two outcomes (either success or failure), then a random variable that takes value 1 in case of success and value 0 in case of failure is a Bernoulli random variable. If you perform an experiment that can have  outcomes and you denote by  a random variable that takes value 1 if you obtain the -th outcome and 0 otherwise, then the random vector  defined asis a Multinoulli random vector. In other words, when the -th outcome is obtained, the -th entry of the Multinoulli random vector  takes value , while all other entries take value .

In what follows the probabilities of the  possible outcomes will be denoted by .

Definition

The distribution is characterized as follows.

Definition Let  be a  discrete random vector. Let the support of  be the set of  vectors having one entry equal to  and all other entries equal to :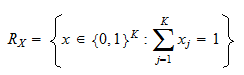Let , ...,  be  strictly positive numbers such thatWe say that  has a Multinoulli distribution with probabilities , ...,  if its joint probability mass function is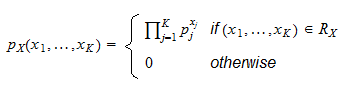

If you are puzzled by the above definition of the joint pmf, note that when  and  because the -th outcome has been obtained, then all other entries are equal to  and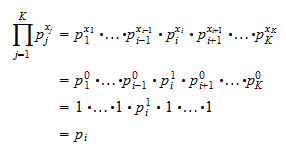

Expected value

The expected value of  iswhere the  vector  is defined as follows:

Proof

Covariance matrix

The covariance matrix of  iswhere  is a  matrix whose generic entry is

Proof

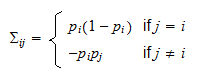
Joint moment generating function

The joint moment generating function of  is defined for any :

Proof

Joint characteristic function

The joint characteristic function of  is

Proof