CF487E Tourists 圆方树、树链剖分

传送门

---

注意到我们需要求的是两点之间所有简单路径中最小值的最小值，那么对于一个点双联通分量来说，如果要经过它，则一定会经过这个点双联通分量里权值最小的点

注意：这里不能缩边双联通分量，样例\(2\)就是一个反例

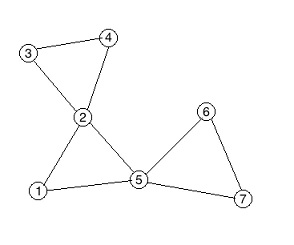
上面这个图如果缩点双会缩成\(3\)个，但是缩边双会将整个图缩成\(1\)个点。

假如我们询问的是\((1,4)\)之间的简单路径，而图中权值最小的点为\(7\)号点，那么如果缩成了边双联通分量，你的答案会是\(7\)号点的权值，意即认为可以走到\(7\)号点，但实际上如果到\(7\)号点，意味着\(5\)号点需要经过\(2\)次，不符合简单路径的要求

所以如果将题意改成“一条边只能经过一次”就是缩边双了

那么我们直接维护圆方树，对于每一个方点使用\(multiset\)维护与它相连的所有圆点的权值，在圆方树上树链剖分计算答案。

当然这样子还是不够的。考虑一种情况：一个圆点连接了一堆方点，然后在这一个圆点上不断进行修改操作，这样每一次修改都会波及一大堆方点的修改，复杂度直接爆炸。

优化：对于所有方点，不去维护它在圆方树上的父亲，那么对于每一次修改，只会波及它在圆方树上的方点父亲。而如果在某一次询问中两点之间的\(LCA\)为方点，还需要额外考虑这个点的父亲的贡献。

#include<bits/stdc++.h>
#define lch (x << 1)
#define rch (x << 1 | 1)
#define mid ((l + r) >> 1)
#define INF 0x7fffffff
//This code is written by Itst
using namespace std;

inline int read(){
    int a = 0;
    char c = getchar();
    bool f = 0;
    while(!isdigit(c) && c != EOF){
        if(c == '-')
            f = 1;
        c = getchar();
    }
    if(c == EOF)
        exit(0);
    while(isdigit(c)){
        a = a * 10 + c - 48;
        c = getchar();
    }
    return f ? -a : a;
}

const int MAXN = 2e5 + 7;
struct Edge{
    int end , upEd;
}Ed[MAXN << 1];
int head[MAXN] , val[MAXN] , N , M , Q , cntEd , cnt;
int topS , ts , st[MAXN] , dfn[MAXN] , low[MAXN];
int ind[MAXN] , rk[MAXN] , fa[MAXN] , dep[MAXN] , son[MAXN] , sz[MAXN] , top[MAXN] , TS;
int Tree[MAXN << 2];
bool vis[MAXN];
vector < int > ch[MAXN];
multiset < int > s[MAXN];

inline void addEd(int a , int b){
    Ed[++cntEd].end = b;
    Ed[cntEd].upEd = head[a];
    head[a] = cntEd;
}

inline void pop(int t , int bot){
    ch[t].push_back(++cnt);
    do{
        ch[cnt].push_back(st[topS]);
        s[cnt].insert(val[st[topS]]);
    }while(st[topS--] != bot);
}

void tarjan(int x , int p){
    st[++topS] = x;
    dfn[x] = low[x] = ++ts;
    vis[x] = 1;
    for(int i = head[x] ; i ; i = Ed[i].upEd)
        if(Ed[i].end != p)
            if(!vis[Ed[i].end]){
                tarjan(Ed[i].end , x);
                low[x] = min(low[x] , low[Ed[i].end]);
                if(low[Ed[i].end] >= dfn[x])
                    pop(x , Ed[i].end);
            }
            else
                low[x] = min(low[x] , dfn[Ed[i].end]);
}

void dfs1(int x , int p){
    fa[x] = p;
    dep[x] = dep[p] + 1;
    sz[x] = 1;
    for(int i = 0 ; i < ch[x].size() ; ++i){
        dfs1(ch[x][i] , x);
        sz[x] += sz[ch[x][i]];
        if(sz[son[x]] < sz[ch[x][i]])
            son[x] = ch[x][i];
    }
}

void dfs2(int x , int t){
    ind[x] = ++TS;
    rk[TS] = x;
    top[x] = t;
    if(!son[x])
        return;
    dfs2(son[x] , t);
    for(int i = 0 ; i < ch[x].size() ; ++i)
        if(ch[x][i] != son[x])
            dfs2(ch[x][i] , ch[x][i]);
}

inline void pushup(int x){
    Tree[x] = min(Tree[lch] , Tree[rch]);
}

void init(int x , int l , int r){
    if(l == r)
        Tree[x] = rk[l] <= N ? val[rk[l]] : *s[rk[l]].begin();
    else{
        init(lch , l , mid);
        init(rch , mid + 1 , r);
        pushup(x);
    }
}

void modify(int x , int l , int r , int tar , int num){
    if(l == r)
        Tree[x] = num;
    else{
        if(mid >= tar)
            modify(lch , l , mid , tar , num);
        else
            modify(rch , mid + 1 , r , tar , num);
        pushup(x);
    }
}

int query(int x , int l , int r , int L , int R){
    if(l >= L && r <= R)
        return Tree[x];
    int minN = INF;
    if(mid >= L)
        minN = min(minN , query(lch , l , mid , L , R));
    if(mid < R)
        minN = min(minN , query(rch , mid + 1 , r , L , R));
    return minN;
}

int work(int x , int y){
    int tx = top[x] , ty = top[y] , minN = INF;
    while(tx != ty){
        if(dep[tx] < dep[ty]){
            swap(x , y);
            swap(tx , ty);
        }
        minN = min(minN , query(1 , 1 , cnt , ind[tx] , ind[x]));
        x = fa[tx];
        tx = top[x];
    }
    if(dep[x] > dep[y])
        swap(x , y);
    minN = min(minN , query(1 , 1 , cnt , ind[x] , ind[y]));
    if(x > N)
        minN = min(minN , val[fa[x]]);
    return minN;
}

inline char getc(){
    char c = getchar();
    while(!isupper(c))
        c = getchar();
    return c;
}

int main(){
#ifndef ONLINE_JUDGE
    freopen("in","r",stdin);
    //freopen("out","w",stdout);
#endif
    cnt = N = read();
    M = read();
    Q = read();
    for(int i = 1 ; i <= N ; ++i)
        val[i] = read();
    for(int i = 1 ; i <= M ; ++i){
        int a = read() , b = read();
        addEd(a , b);
        addEd(b , a);
    }
    tarjan(1 , 0);
    dfs1(1 , 0);
    dfs2(1 , 1);
    init(1 , 1 , cnt);
    while(Q--)
        if(getc() == 'A')
            printf("%d\n" , work(read() , read()));
        else{
            int a = read() , b = read();
            if(a != 1){
                s[fa[a]].erase(s[fa[a]].find(val[a]));
                s[fa[a]].insert(b);
                modify(1 , 1 , cnt , ind[fa[a]] , *s[fa[a]].begin());
            }
            val[a] = b;
            modify(1 , 1 , cnt , ind[a] , b);
        }
    return 0;
}