【实践报告】Linux实践三
Linux实践——程序破解
一、掌握NOP、JNE、JE、JMP、CMP汇编指令的机器码
- NOP:NOP指令即“空指令”。执行到NOP指令时,CPU什么也不做,仅仅当做一个指令执行过去并继续执行NOP后面的一条指令。(机器码:90)
- JNE:条件转移指令,如果不相等则跳转。(机器码:75)
- JE:条件转移指令,如果相等则跳转。(机器码:74)
- JMP:无条件转移指令。段内直接短转Jmp short(机器码:EB)段内直接近转移Jmp near(机器码:E9)段内间接转移Jmp word(机器码:FF)段间直接(远)转移Jmp far(机器码:EA)
- CMP:比较指令,功能相当于减法指令,只是对操作数之间运算比较,不保存结果。cmp指令执行后,将对标志寄存器产生影响。其他相关指令通过识别这些被影响的标志寄存器位来得知比较结果。
二、掌握反汇编与十六进制编程器
- 指令“objdump -d login”查看反汇编代码
将750e改为7500
注:为了跳过口令检查,也就是无论比较的结果如何,都正常登陆。
jne是条件跳转,如果条件满足,则跳转;
jne下两行可知是输出内容;
jmp是跳转语句(没有条件,则直接跳转)
jmp下两行也是输出内容。
jne表示当比较不相等时,跳转。也就是说,当输入与已存口令不相等时,跳转到jmp下一行mov,如果比较结果相等,则执行jne下两行mov、call行,说明,执行mov、call行输出的为“right”。
vi打开login,输入“:%!xxd”



输入:/750e查找到那个位置,比对四周,确定位置后将其修改为7500

输入“:%!xxd -r”保存
输入“:wq”保存
运行login测试结果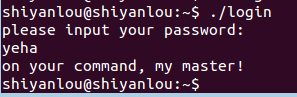
【实践报告】Linux实践三的更多相关文章
- 20172328《程序设计与数据结构》实验三 敏捷开发与XP实践报告
20172328<程序设计与数据结构>实验三 敏捷开发与XP实践报告 课程:<程序设计与数据结构> 班级: 1723 姓名: 李馨雨 学号:20172328 实验教师:王志强 ...
- LINUX第三次实践:程序破解
LINUX第三次实践:程序破解 标签(空格分隔): 20135328陈都 一.掌握NOP.JNE.JE.JMP.CMP汇编指令的机器码 NOP:NOP指令即"空指令".执行到NOP ...
- linux第三次实践:ELF文件格式分析
linux第三次实践:ELF文件格式分析 标签(空格分隔): 20135328陈都 一.概述 1.ELF全称Executable and Linkable Format,可执行连接格式,ELF格式的文 ...
- linux实践之ELF文件分析
linux实践之ELF文件分析 下面开始elf文件的分析. 我们首先编写一个简单的C代码. 编译链接生成可执行文件. 首先,查看scn15elf.o文件的详细信息. 以16进制形式查看scn15elf ...
- Linux实践:文件破解
Linux实践:文件破解 标签(空格分隔): 20135321余佳源 一.掌握NOP.JNE.JE.JMP.CMP汇编指令的机器码 NOP:NOP指令即"空指令".执行到NOP指令 ...
- [Linux实践] macOS平台Homebrew更新brew update卡死,完美解决
[Linux实践] macOS 平台 Homebrew 更新 brew update 卡死,完美解决 版本2020.01.05 摘要: 使用brew install [软件包]安装软件包时,卡在Upd ...
- 第04项目:淘淘商城(SpringMvc+Spring+Mybatis) 的学习实践总结【第三天】
淘淘商城(SpringMVC+Spring+Mybatis) 是传智播客在2015年9月份录制的,几年过去了.由于视频里课上老师敲的代码和项目笔记有些细节上存在出入,只有根据日志报错信息作出适当的调 ...
- linux实践之程序破解
linux实践之程序破解 这次的实践是文件破解,让我们从login可执行文件开始吧! 首先我们执行一下这个可执行程序 ①我们希望在不知道密码的情况下,能够登陆进去.且无论密码是什么,都是提示“on y ...
- atitit.报告最佳实践oae 和报告引擎的选择
atitit.报告最佳实践oae 与报表引擎选型 1. 报表的基本的功能and结构 2 1.1. 查询设计器(配置化,metadata in html) ,anno 2 1.2. 查询引擎 2 1.3 ...
随机推荐
- mysql覆盖索引详解
覆盖索引的定义: 如果一个索引包含(或覆盖)所有需要查询的字段的值,称为‘覆盖索引’.即只需扫描索引而无须回表. 只扫描索引而无需回表的优点: 1.索引条目通常远小于数据行大小,只需要读取索引, ...
- NSObject
一.前言 该博客里面的方法均是看着苹果官方的API来解释的,一般都是常用的方法如有问题,请指出. 二.简介: 该类集成的是其本身,大家可以从任何一个类去向上追溯,都会发现最终的父类都是NSObject ...
- Java计模模式之六 ----- 组合模式和过滤器模式
前言 在上一篇中我们学习了结构型模式的外观模式和装饰器模式.本篇则来学习下组合模式和过滤器模式. 组合模式 简介 组合模式是用于把一组相似的对象当作一个单一的对象.组合模式依据树形结构来组合对象,用来 ...
- Unity3D中自带事件函数的执行顺序
在Unity3D脚本中,有几个Unity3D自带的事件函数按照预定的顺序执行作为脚本执行.其执行顺序如下: 编辑器(Editor) Reset:Reset函数被调用来初始化脚本属性当脚本第一次被附到对 ...
- 拓普微智能TFT液晶显示模块
关键词: 串口屏, 液晶屏, TFT,人机界面 概述: 智能模块(Smart LCD)是专为工业显示应用而设计的TFT液晶显示模块. 模块自带主控IC.Flash存储器.实时嵌入式操作系统,客户主机可 ...
- Nginx主程序使用介绍
守护进程和服务 <br\>在首次运行Nginx之前,了解此应用程序的性质很重要. 有两种类型的计算机应用程序 – 那些需要用户输入,因此在前台运行,另一种在后台运行. Nginx是后一种类 ...
- 【美妙的Python之三】Python 对象解析
美妙的Python之Python对象 简而言之: Python 是能你无限惊喜的语言.与众不同. Python对象概念的理解,是理解Python数据存储的前提.Pyth ...
- $Matrix-Tree$定理-题目
$Matrix-Tree$ 其实矩阵树的题挺好玩的,一些是套班子求答案的,也有一些题目是靠观察基尔霍夫矩阵性质推式子的. 文艺计算姬:https://www.lydsy.com/JudgeOnline ...
- e 的由来
https://www.zhihu.com/question/20296247 对数的发现 很多科学家发现对数螺线在自然界中广泛存在.从大如星系.台风,到小如花朵.海螺……宇宙中到处都是对数螺线的身影
- leetcode46. Permutations 、47. Permutations II、 剑指offer字符串的排列
字符串排列和PermutationsII差不多 Permutations第一种解法: 这种方法从0开始遍历,通过visited来存储是否被访问到,level代表每次已经存储了多少个数字 class S ...
