TSP-UK49687

Copied From：http://www.math.uwaterloo.ca/tsp/uk/index.html

Shortest possible tour to nearly every pub in the United Kingdom.

Line drawing of the optimal route. Click.

Previous Next

• Click for an image of the full tour, or here for a high-resolution image.
• See the tour in a 39-second video.
• Move around the tour in an interactive map.

Impossible.
That's what you hear when you set out to solve a traveling salesman problem.
In February 2018, the Washington Post reported that it would take at least 1,000 years for a computer to find an optimal route to only 22 points.
So we were excited a couple of years ago when we computed the shortest possible walk to 24,727 pubs.
A ton of math and 10 months of time on a fast computer brought home the tour.
The computation even received fun coverage in The Guardian (October 21, 2016), The Sun (October 22, 2016), and other UK newspapers.

 

<figcaption="figure-caption">Pub tour coverage in The Guardian and The Sun.

 

Then the comments and email started to roll in.
Several thousands of them.
Starting with the first messages in The Guardian, posted several minutes after Will Coldwell's article appeared.

Wot no Turf Tavern, Oxford? (10:26)

There don't seem to be many pubs in Northern Ireland. (10:30)

Pretty sure there are pubs on Skye and Islay, among other locations that appear to have been missed. (10:33)

Yeh, there are definitely pubs up the west side of Loch Lomond too, like the Oak Tree Inn in Balmaha, that have been missed.
So called 'experts', eh? (10:38)

And on and on.
The problem was the following.
When we gathered data in the fall of 2015, we estimated our algorithms could handle a TSP instance with about 25,000 points.
So, starting with the great Pubs Galore
data base, we filtered out places based on names, for example, any
listing that contained the words "Hotel" or "Inn" were tossed out.
That was a mistake.
It would have been better to choose blindly 25,000 stops from the Pubs
Galore list.
The name-pruning method hit parts of the UK much harder than others.
For example, we missed every pub on the Isle of Skye.
The Scots were not shy about letting me know.

 

 

But we are applied mathematicians.
If the British want a tour through more pubs, then that's what we will
deliver.
It took another year-and-a-half of work and 250 years of computer time
(up from the earlier tour's 10-month computation), but we now have a
shortest-possible walking tour through nearly every UK pub.
A total of 49,687 places to get a pint.
The trip will take you 63,739,687 meters, or about a sixth of the
distance to the moon.
But, hey, that's what you asked for.
And, along the way, we created new algorithms that can help to optimize
plenty of mathematical models, well beyond the traveling salesman.

Research Team

William Cook, Combinatorics and Optimization, University of Waterloo, Canada
Daniel Espinoza, Gurobi Optimization, USA

Marcos Goycoolea, School of Business, Universidad Adolfo Ibanez, Chile
Keld Helsgaun, Computer Science, Roskilde University, Denmark

Nearly Every Pub

We can't really list every UK pub.
Drinking houses are opening and closing their doors each week.
But we want to reach nearly all of the them.
So how many pubs are there?
A recent BBC News article contained the following chart, based on data from the British Beer and Pub Association

 

 

A slow, but steady, decrease in the number of pubs, with just over
50,000 reported in 2016.
This number matches nicely the "almost 50,000 pubs" remark made in a
Pubs Galore Twitter post, in a response to The Guardian's article on the
24,727-pub tour.

 

 

The Twitter post agrees with the Pubs Galore page (April 16, 2018) reporting "Pubs Galore currently has 49546 open pubs listed".
The Open Pubs data project reports a bit more, 51,566 in total, based on data from the Food Standard Agency's Food Hygine Ratings.
So around around 50,000 pubs should be the target.
Good, since we were able to grab locations of 49,704 sites from the Pubs
Galore data base on January 12, 2017.
From this set we removed 17 pubs that could not be reached with Google
walking directions.
Ten of these removed listings are from the Isles of Scilly and several
others are from airport terminals. You can find a list of the 17 pubs on
the Data page.

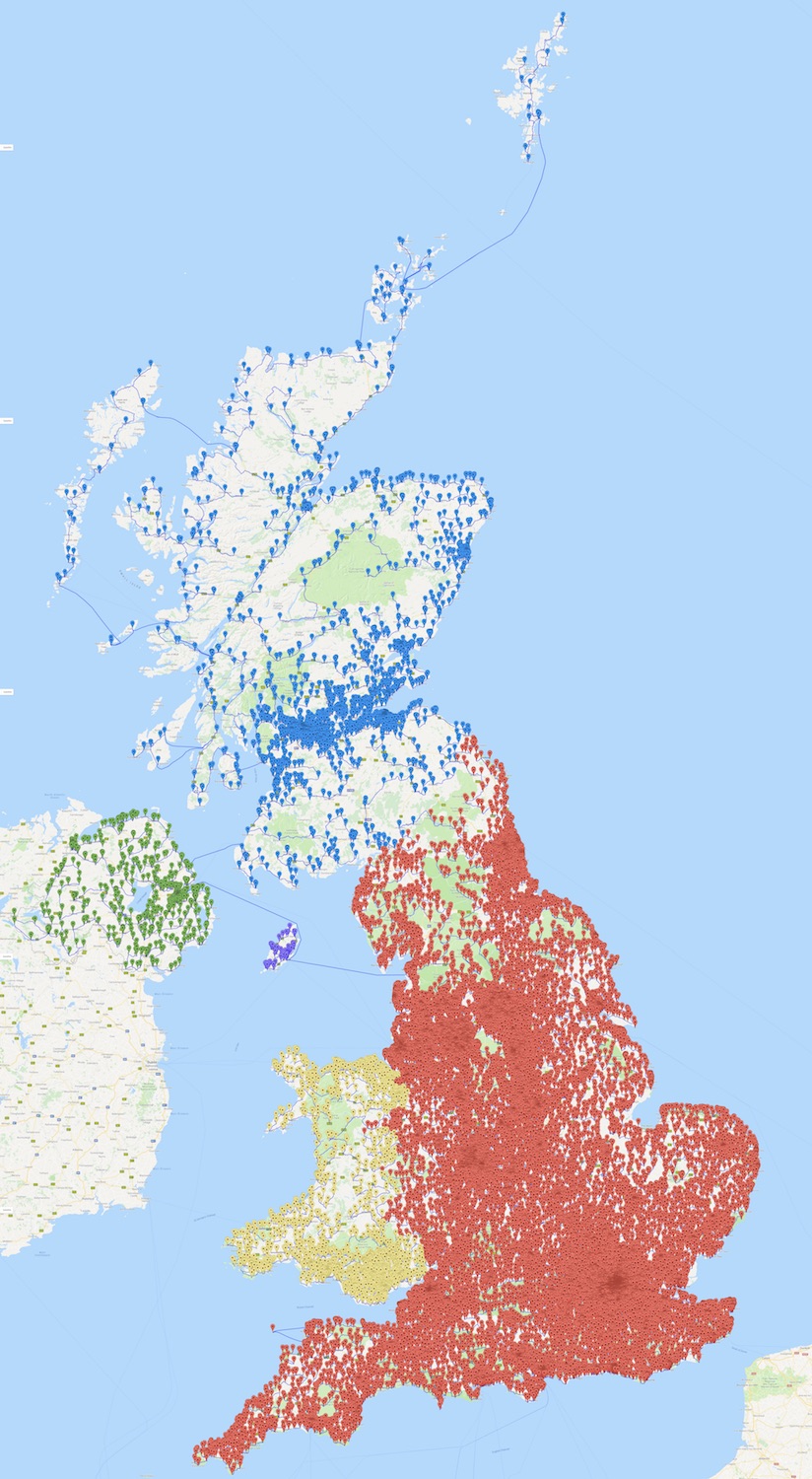
The following two images display Scottish pubs in the 24,727-pub tour, from 2016, and in the new tour.
No wonder the Scots were upset.

<figcaption="figure-caption">Much better coverage with the data set. Click for a larger image.

I can remark that the Turf Tavern in Oxford is now stop #36,233 on the
tour (comment 10:26), there are now 981 stops in Northern Ireland
(comment 10:30), we have 26 pubs on the Isle of Skye (comment 10:33),
and the Oak Tree in Balmaha is stop #14,874 (comment 10:38).
So there!

Walking Distances

For pub-to-pub distances, we rely on the fantastic service provided by Google Maps.
Ask Google for the shortest way to walk from The Fiddler's Elbow over to
The Bald Face Stag and it will respond with excellent step-by-step
directions.
The level of detail covered by Google Maps is amazing.

We use walking distances for two reasons.
First, we obviously don't want to encourage anyone to be behind the
wheel of motorcar after visiting a pub.
Secondly, with walking distances it doesn't matter the direction you
travel, from The Elbow to The Stag or back from the The Stag to The
Elbow.
This is not always true for driving distances, particularly when
navigating London's one-way streets.
You can find more information on this in the Data page.

So this is our challenge.
Using geographic coordinates of 49,687 pubs provided by Pubs Galore and
measuring the distance between any two pubs as the length of the route
produced by Google Maps, what is the shortest possible tour that visits
all 49,687 and returns to the starting point?

We need to make one final assumption.
It is something only a mathematician would consider, but we have to
assume that the route Google suggests for walking between The Fiddler's
Elbow and The Bald Faced Stag is no shorter than the geometric distance
between the points, that is, the route a smart crow would fly.
This makes it conceivable to solve the problem without actually asking
Google for the distance to travel between each pair of pubs, an
important consideration since there are 1,232,159,688 pairs and Google
puts caps on the number of distance requests per day.

This is the problem we have solved.
The optimal tour has length 63,739,687 meters.
Our result is that there simply does not exist any pub tour that is even
one meter shorter (measuring the length using the distances we obtained
from Google) than the one produced by our computation.
It is the solution to a 49,687-stop traveling salesman problem (TSP).

The Tour

A list of the 49,687 pubs, one after the other, in the correct order,
resembles a good-sized phone book and does not convey the structure and
complexity of the tour.
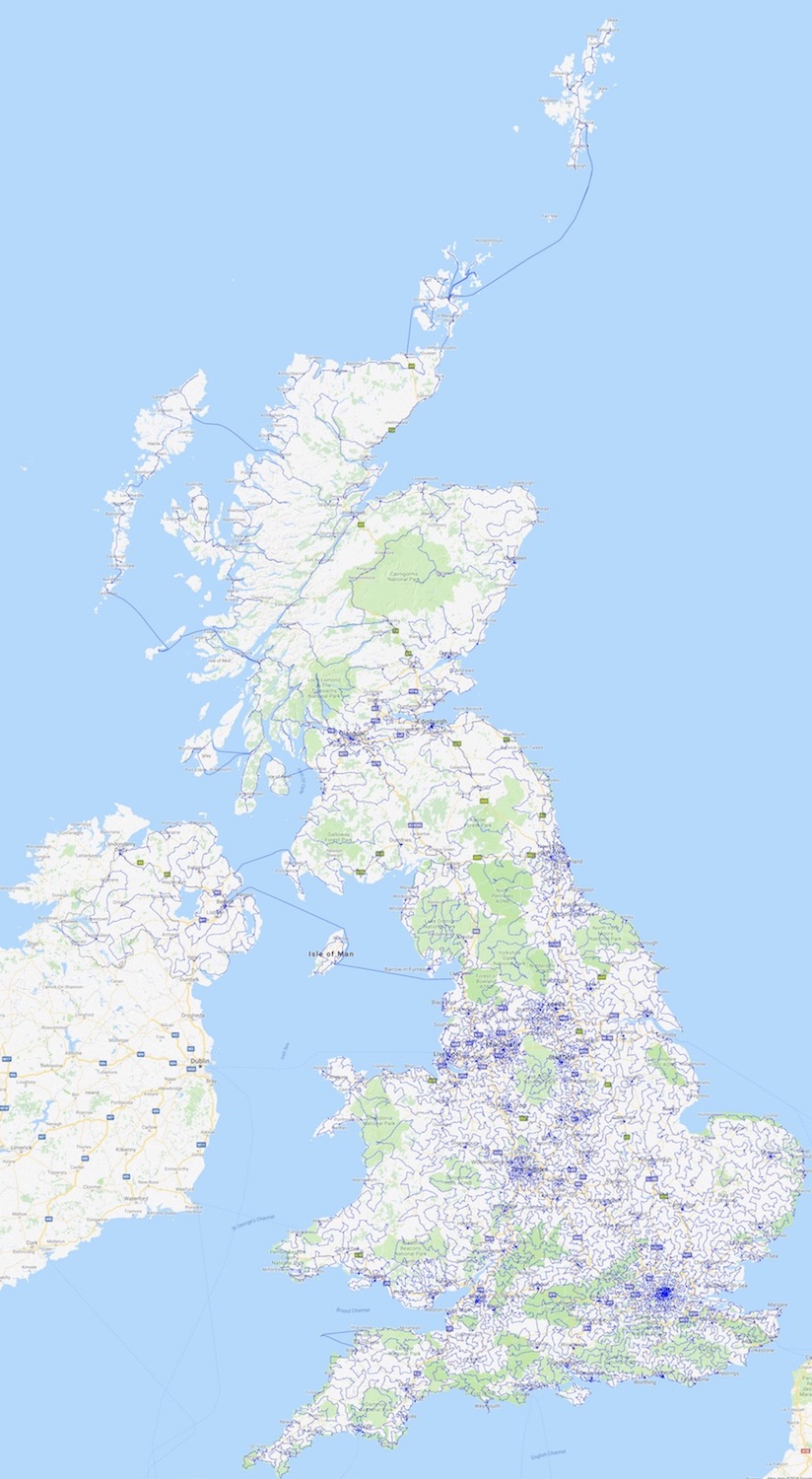
A better way to get a quick view is to study the two images below, where
the tour is depicted as a thin blue line.
The drawing on the left includes the pub locations as markers and the
one on the right is just the line drawing.
Clicking on either image gives a much larger version.

Click for larger view.

Click for a larger view.

You see that we obviously cannot walk several of the indicated routes:
to reach the Isle of Man, Northern Ireland, and the islands of Scotland,
the tour uses scheduled passenger-ferry routes provided by Google's
direction services.

To give a detailed view, we make use of the Google Maps drawing tools to
display an interactive version of the tour, where you can zoom in and
pan from one region to another.
The link is given below, but first a word of warning: the map contains a
great deal of information and it can take a minute or so to load.
We provide tips for using the map on the Tour page.

 

<figcaption="figure-caption">Click image for an interactive map.

 

If the map refuses to load for you, please have a look at the Tour page, where you can find smaller, regional maps, as well as further information about the route.

Optimality

How do we know the tour is the shortest possible?
Clearly we did not check every tour, one by one by one.
The first thing you learn about the TSP is that it is impossible to solve in this way.
If you have N cities, then, starting from any point, you have N-1 possibilities for the second city.
Then N-2 possibilities for the third city, and so on.
The total number of tours is obtained by multiplying these values: N-1 x (N-2) x (N-3) x . . . x 3 x 2 x 1.
Now this is a big number.
For this new (larger) pubs problem, it is roughly 3 followed by 211,761 zeroes, as computed by WolframAlpha.
That is in an unimaginably large number of possibilities.
Even for 50 cities, the world's fastest supercomputer has no hope of going through the full count of tours one by one to pick out the shortest.
(This is the basis for the 1,000-year estimate reported in the Washington Post.)

But this by itself does not mean we can't possibly solve an example of
the TSP.
If you have 50 words to put into alphabetical order, you don't worry
about the 50 x 49 x 48 x ... x 3 x 2 x 1 possible lists you could
create.
You just sort the words from first to last and build the one correct
list among the huge number of possibilities.

For the TSP we don't know of any simple and fast solution method like we have for sorting words.
And, for technical reasons, it is believed that there may be large, nasty TSP examples that no one can ever solve.
(If you are interested in this and could use an extra $1,000,000, check out the P vs NP problem.)
But if you need to plot a 50-point route for a holiday or to compute the
order of 10,000 items on a DNA strand, then mathematics can help, even
if you need the absolute shortest-possible solution.

The way to proceed is via a process known as the cutting-plane method.
If you have 4 minutes to spare, and don't mind my squeaky voice, click here (109 MByte file) for a video that introduces the method and how it is used to attack the TSP.

<figcaption="figure-caption">TSP lecture at JMM 2018. Photo by Tim Chartier.

The full lecture Information, Computation, Optimization: Connecting the Dots in the Traveling Salesman Problem is available on YouTube and on the web page for the 2018 Joint Mathematics Meetings.
(Warning: At the time of the lecture, January 11, 2018, we were deep in
the middle of the pubs computation and I didn't yet know if it would
have a happy ending.)

I expect you are in a hurry, however, so here is how I describe the process in a short piece in Scientific American

The idea is to follow Yogi Berra's advice "When you come to a fork in
the road, take it." A tool called linear programming allows us to do
just this, assigning fractions to roads joining pairs of cities, rather
than deciding immediately whether to use a road or not. It is perfectly
fine, in this model, to send half a salesman along both branches of the
fork.

The process begins with the requirement that, for every city, the
fractions assigned to the arriving and departing roads each sum to one.
Then, step-by-step, further restrictions are added, each involving sums
of fractions assigned to roads. Linear programming eventually points us
to the best decision for each road, and thus the shortest possible
route.

Our pubs computation used a improved version of the Concorde
implementation of the TSP cutting-plane method.
Even if you are in a hurry, you might want to see for yourself how the
process solves smaller examples on an iPhone or iPad by downloading the
free Concorde App.

Our computation also adopted Keld Helsgaun's LKH
code.
LKH combines a powerful local-search technique with a genetic algorithm
to produce a high-quality tour.
Remarkably, in the case of the UK pubs problem, LKH delivered, early in
our computation, what proved to be the optimal solution.
The bulk of our work, spanning 250 years of computation time, was to
prove there could be no shorter tour than the one found by Keld's LKH
code.

In working with road data, we were faced with the challenge of finding
the correct TSP solution even though we could not possibly ask Google
for all 1,232,159,688 pairs of pub-to-pub distances.
In our earlier work on the 24,727-pubs tour, we used an ad hoc,
trial-and-error, process to gather a sufficient number of Google
pub-to-pub distances to permit the computation to go through.
(See the UK24727 page.)
For this new, much more difficult, problem, we developed algorithms to
automate this portion of the computation, requesting pub-to-pub
distances for 2,214,453 pairs, only 1/500th of the total number.
Many thanks to Google for providing this data for us!

The distance-gathering part of the computation was completed on February
15, 2018.
Four days later, LKH had produced 6 different tours, each having length
63,739,687 meters.
These tours (or, more precisely, their common length) served as a beacon
for Concorde and the cutting-plane method, allowing us to have an
excellent measure of the progress we were making towards the solution of
the problem.
What followed was a long process to build a strong linear-programming
relaxation for the pubs TSP, utilizing a 288-core network of computers
(whenever it was not otherwise occupied).
This process ended on May 16, 2017, after a total (adding up the time
spent on each core of the network) of approximately 50 years of
computation.
The result was that we now knew for certain that no tour could be
shorter than 63,732,189 meters.
So we knew that the LKH tours were at most 7.5 kilometers longer than an
optimal route.

To finish off the problem, we turned to Concorde's branch-and-bound
search procedure.
In this process, the collection of tours is repeatedly subdivided and
the cutting-plane method is applied to the resulting TSP subproblems.
The simplest form of the division is to select a pair of pubs, say The
Black Dog and The Duke of Cornwall in Weymouth, and consider first only
tours where the two pubs are visited consecutively, then consider only
tours where, between the stops at The Dog and The Duke, we drop in on at
least one other pub along the way.
This selection divides the set of all tours neatly into two subsets.

In this this final phase of the computation, we processed 557,271
subproblems.
A big part of the challenge was in making estimates of the remaining
computation time, to determine whether or not we would be able to solve
the problem before we all reached retirement age.
The computation finally finished on March 5, 2018, nearly 14 months
after we gathered the data from Pubs Galore.
The total amount of computer time for this branch-and-bound portion of
the computation was roughly 200 years, bringing the total to 250 years
(if carried out on a single processor core of a Linux server).

Click here to see a drawing of the search tree, where the position of a subproblem corresponds to the value of its fractional tour.
For a closer look, here is a pdf file for the tree.

49,687¥ Reward

We have applied some 64 years of mathematics research (going back to the 1954 paper by Dantzig, Fulkerson, and Johnson)
to obtain a proof that we have a shortest-possible tour.
But it was a huge computation and it wouldn't hurt to have more eyes on
this particular example of the TSP.
So, we offer 49,687 Japanese Yen to the first person who can find a tour
that is even 1 meter shorter than our 63,739,687-meter route.
Let's call it an even 50,000 ¥.
I have the bank notes ready to ship out.

<figcaption="figure-caption">50,000 ¥ for a shorter tour.

You can find details on the input for the problem on the Data
page.
But please don't view this as a realistic way to earn enough cash to
pick up a pint at the first 100 pubs of the tour.
We are confident our solution is correct.
I should mention that the branch-and-bound run was made with the input
length of 63,739,688, that is, 1 greater than the length of the LKH
tours.
In this way, as another check, the branch-and-bound search had to itself
produce a tour of length 63,739,687.
Which it did, on the final day of the search.

Data

If you are interested in creating your own local pub tour, the best bet for data is to go back to the original sources, Pubs Galore for locations and Google Maps
for up-to-date walking distances.
But the information provided by these sources changes over time.
Therefore, to document the 49,687-stop TSP instance we have solved, we
provide the raw data needed to reproduce the travel distances on the Data page.

Tour-Finding History

Early computational studies focused on the most natural class of
salesman problems: select an interesting group of cities, look up
point-to-point distances in a road atlas, and have a go at finding the
shortest tour.
Record-setting solutions were found by legendary figures in applied
mathematics, operations research, and computer science.

• 49 USA cities in 1954 by George Dantzig, Ray Fulkerson, and Selmer Johnson.
• 57 USA cities in 1970 by Michael Held and Richard Karp.
• 120 German cities in 1977 by Martin Groetschel.

The first reference, in particular, is widely viewed as the most
important paper in the history of the broad fields of discrete
optimization and integer programming.
The links are to technical research papers.
For lighter viewing, have a look at our Road Trips page.

In the late 1970s, the focus switched to geometric examples of the TSP,
where cities are points drawn on a sheet of paper and travel is measured
by straight-line distances.
The reasons were twofold.
First, with over 100 stops it became difficult to obtain driving
distances along road networks: printed road atlases included distances
only for major cities.
Second, there were classes of industrial problems that neatly fit into
the geometric TSP setting.
Indeed, the next world record, set in 1980 by Harlan Crowder and Manfred Padberg, consisted of locations of 318 holes that had to be drilled into a printed-circuit board.

Geometric TSP instances, arising in applications and from geographic locations, were gathered together in the TSPLIB by Gerhard Reinelt in the early 1990s.
This collection became the standard test bed for researchers.
The largest of the instances, having 85,900 points arising in a VLSI application, was solved by Applegate et al. in 2006.

The geometric data sets are worthy adversaries, but the large industrial instances have points clustered into straight lines.
These examples are punching below their weight, likely missing aspects of the complexity of the road TSP challenges.

Next Up: Travel to 2,079,471 Stars

A main research interest, for us, in solving road-distance examples of
the TSP was to establish whether or not optimization techniques, that
since the 1970s have been directed towards geometric examples, would
carry over to the non-geometric data provided by Google.
The great difficulty we encountered with the pubs example made for
fruitful research.

But road examples are also two dimensional, with points specified by the
latitude and longitude of each pub location.
So what about 3-dimensional data, where points are given by
xyz-coordinates and travel is measured by the straight-line Euclidean
distance between pairs of points?
Work here might also lead to interesting optimization research.

Fun examples of 3D travel would be to mimic the voyages of the starship Enterprise, going from star to star.
Fortunately, astronomers have interesting data bases, with sufficient information to give the approximate 3D positions of stars.
Off we go!

As a warm up, we first computed an optimal tour to visit the nearest 10,000 stars to our sun.
You can see the points for the star locations and the edges of the tour in the following 9-second video.

 

After that, we stepped up to a 109,399-star instance from the HYG Database constructed by David Nash.
(Many thanks to Bob Vanderbei for directing us to this collection.)
We were able to solve this instance in September 2017.

<figcaption="figure-caption">Close-up view of the 109,399-star TSP. Click for a larger image.

You can find the data for the 109,339-star problem, in TSPLIB format, here.
This is now the largest solved instance of the traveling salesman
problem.
(Actually, we also solved the TSP for the full 119,614 entries of the
HYG data base, but for 10,275 of these stars the distance information is
missing: the xyz-coordinates in the data base place these 10,275 points
all at distance 100,000 parsecs from the Earth, whereas each of the
remaining stars has distance less than 1,000 parsecs, so it is really
like a separate TSP instance on the outer rim.)

It is interesting that the 109,339-star example, despite its size, was much easier for our methods than the UK pubs instance.
In fact, we solved it by stealing time from the UK computation during the summer of 2017.
The total running time for the computation was 7.5 months.

But a nice thing about computational research is that you can always go
bigger.
If 109,339 stars was not enough to spark the creation of new
optimization techniques, then how about a 2,079,470-star instance
obtained from combining data from the European Space Agency's Gaia Mission together with the bright stars from the HYG data base?

The full Gaia Data Release 1 reports on an amazing total of
1,142,679,769 stars.
Most of the entries do not contain sufficient information to estimate
distances to the corresponding stars (but future work in the ESA Gaia
project should make such estimates possible).
However, for 2,057,050 stars in the TGAS (Tycho-Gaia Astronomic Solution) collection, the Gaia data does permit distance estimations.
The process used to obtain these distances is described in the following research paper.

Estimating distances from parallaxes. III. Distances of two million stars in the Gaia DR1 Catalogue
Tri L. Astraatmadija and Coryn A. L. Balier-Jones
The Astrophysical Journal, Volume 833, Number 1 (2016).

We use the Astraatmadija-Balier-Jones distance estimates to obtain coordinate positions for the TGAS stars.
The data set for our TSP instance is given in the gzipped file gaia2079471.tsp.gz.

Studying this large-scale example of the TSP is on-going work, together with David Applegate (Google) and Keld Helsgaun (Roskilde University).

We currently have a tour of length 28,884,456.3 parsecs, found with a parallel version of LKH.
We also know, via a parallel application of the cutting-plane method, that there is no tour shorter than 28,883,773.4 parsecs.
That means our tour is at most 1.000024 times longer than a optimal route through the two million stars.
That fourth zero in the approximation factor is the money ball: leading commercial mixed-integer programming solvers, such as CPLEX and Gurobi, declare, by default, that a problem is solved if they obtain a solution and a bound that differ by at most a factor of 1.0001.
We are already 4 times closer.
But we are shooting for a shortest-possible route, not just a good approximation.

It will certainly be difficult to decrease substantially the gap between
the length of the tour and the lower bound.
Improvements will come only through advancements in general techniques
for the solution of optimization problems of enormous scale.
That is what this area of research is all about.

The Big Picture

The work was carried out over the past three-and-a-half years.
We use the UK pubs data, and other large examples of the traveling
salesman problem, as a means for developing and testing general-purpose
optimization methods.
The world has limited resources and the aim of the applied mathematics
fields of mathematical optimization and operations research is to create tools to help us to use these resources as efficiently as possible.

For general information on mathematical modeling and its impact on
industry, commerce, medicine, and the environment, we point you to a
number of societies that support mathematics research and education:
American Mathematical Society,
Mathematical Association of America,
Mathematical Optimization Society,
INFORMS (operations research),
London Mathematical Society,
and SIAM (applied mathematics).

Acknowledgements

Google Maps provided the
interface between the real world and the abstract mathematical model of
the TSP.
The engineers at Google do all of the heavy lifting in dealing with
paths, roads, traffic circles, construction sites, closures, detours,
and on and on.

Pubs Galore - The UK Pub Guide is the source for the locations of the stops on our TSP tour.
No matter where you are in the UK, the Pubs Galore site will help you find a cozy place for a meal and a drink.

The huge number of linear-programming models that arose in the computation were solved with the IBM CPLEX Optimizer.
Many thanks to IBM for making their great software freely available for academic research.

The work of William Cook was supported by a Discovery Grant from the Natural Sciences and Engineering Research Council (NSERC) of Canada.

Other Road Trips

US History Tour

See 49,603 sites from the National Register of Historic Places.

UK24727 Tour

An optimal tour to 24,727 pubs in the UK. Solved in August 2016.

Queen of College Tours

Drive to all 647 campuses on Forbes' list of America's Top Colleges.

Pokemon Go Tours

How to catch 'em all. As quickly as possible.