【从最简单的做起】——波利亚

请看下面三道循序渐进不断加细的题。

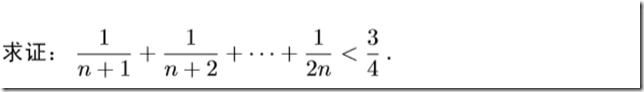
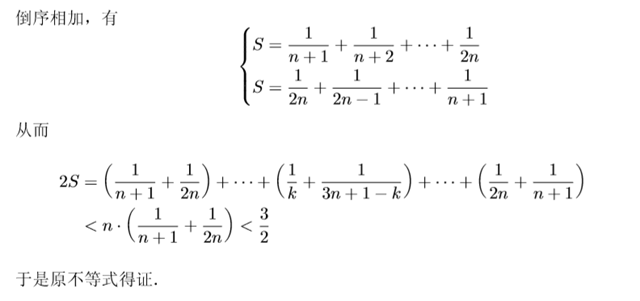
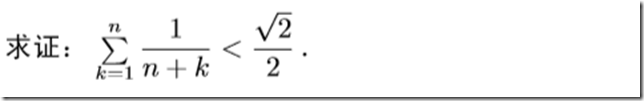
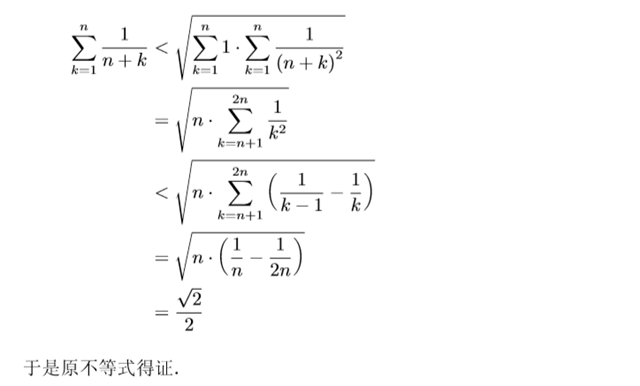
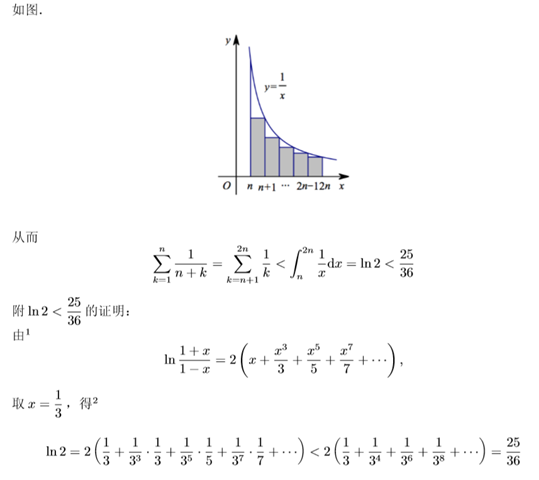
评:随着右边的不断加细，解决问题的方法也越来越“高端”.当然最佳值$ln2$我们可以用相对

容易的方法来证明:

$\because ln(2k+1)-ln(2k-1)>\frac{1}{k}$两边$k$从$n+1$取到$2n$得$$ln2>\sum_{k=1}^{n}{\frac{1}{n+k}}$$

MT【53】对数平均做数列放缩的更多相关文章

  1. MT【26】ln(1+x)的对数平均放缩

    评:1.某种程度上$ln(1+x)\ge \frac{2x}{2+x}$是最佳放缩. 2.这里涉及到分母为幂函数型的放缩技巧,但是不够强,做不了这题.

  2. MT【148】凸数列

    (2018浙江省赛13题) 设实数$x_1,x_2,\cdots,x_{2018}$满足$x_{n+1}^2\le x_nx_{n+2},(n=1,2,\cdots,2016)$和$\prod\lim ...

  3. MT【307】周期数列

    (2017浙江省数学竞赛) 设数列$\{a_n\}$满足:$|a_{n+1}-2a_n|=2,|a_n|\le2,n\in N^+$证明:如果$a_1$为有理数,则从某项后$\{a_n\}$为周期数列 ...

  4. hdu5988（费用流，对数相乘做加法）

    题意:一个网络流的图,有n个点,从1~n,然后m条边,每个点有两个值,一个是人的数量si一个是饭的数量bi.每条m边有容量ci,还有走上去可能踩断电线的概率pi(第一次踩上去没有事,之后都要p概率). ...

  5. MT【256】2016四川高考解答压轴题

    (2016四川高考数学解答压轴题)设函数$f(x)=ax^2-a-\ln x,a\in R$. 1)讨论$f(x)$的单调性;2)确定$a$的所有可能值,使得$f(x)>\dfrac{1}{x} ...

  6. [PHP] 2018年终总结

    去掉敏感信息后的不完整版 ==========================================================================2018年12月29日 记 ...

  7. 论文阅读笔记三十：One pixel attack for fooling deep neural networks（CVPR2017）

    论文源址:https://arxiv.org/abs/1710.08864 tensorflow代码: https://github.com/Hyperparticle/one-pixel-attac ...

  8. [代码解析]Mask R-CNN介绍与实现(转)

    文章来源 DFann 版权声明:如果你觉得写的还可以,可以考虑打赏一下.转载请联系. https://blog.csdn.net/u011974639/article/details/78483779 ...

  9. InnoDB引擎中的索引与算法9

    5.1 InnoDB支持以下几种常见的索引: B+树索引 全文索引 哈希索引(自适应哈希索引) 关于哈希索引的说明: -- 1.InnoDB的哈希索引是自适应的,其根据表的使用情况自动生成哈希索引,不 ...

随机推荐

  1. springbootAdmin+eureka集群+swagger

    请移步githubb下载源码.知识共享.(https://github.com/yivvonllh) 或者直接git下载(https://github.com/yivvonllh/spring-clo ...

  2. SQL Server中比较末尾带有空格的字符串遇到的坑 （转载）

    最近发现SQLServer中比较字符串的时候 如果字符串末尾是空格 那么SQLServer会无视那些空格直接进行比较 这和程序中平时的字符串判断逻辑不统一 );set @a=N'happycat198 ...

  3. (转)Putty server refused our key的三种原因和解决方法

    原文 上一篇博文介绍了使用Putty免密码登录,我后面试了另一台虚拟机,结果putty显示错误server refused our key(在linux下则表现为仍需要输入密码),搜索了下,很多人都遇 ...

  4. 数列分块入门九题（一）：LOJ6277~6279

    Preface 分块,一个神奇的暴力算法.可以把很多\(O(n^2)\)的数据结构题的暴力优化到常数极小的\(O(n\sqrt n)\).当一些毒瘤题无法用线段树,主席树,平衡树,树状数组...... ...

  5. 【强化学习】python 实现 q-learning 例三（例一改写）

    本文作者:hhh5460 本文地址:https://www.cnblogs.com/hhh5460/p/10139738.html 例一的代码是函数式编写的,这里用面向对象的方式重新撸了一遍.好处是, ...

  6. EF_DataFrist遇到的问题

    正在 Code First 模式下将此上下文与从 EDMX 文件生成的用于 Database First 或 Model First 开发的代码一起使用.这将无法正常工作.若要解决此问题,请不要删除引 ...

  7. Let the Balloon Rise HDU水题

    题意 让你统计字符串最多的那个串,并输出 分析 直接用map统计,不断更新最大值即可 代码 #include<iostream> #include<algorithm> #in ...

  8. A. Vasya and Chocolate

    链接 [http://codeforces.com/contest/1065/problem/A] 分析 一个公式完事 代码 #include<bits/stdc++.h> using n ...

  9. Notes of Daily Scrum Meeting（12.24）

    平安夜了,我们还在这里辛苦地赶代码,整个人都不好了... 今天的团队任务总结如下: 团队成员 今日团队工作 陈少杰 寻找大神帮助,调试网络连接 王迪 建立搜索的UI界面,把算法加入进去 金鑫 调试网络 ...

  10. 《Linux内核设计与实现》读书笔记 3

    第三章 进程管理 3.1进程 概念: 进程:处于执行期的程序.但不仅局限于程序,还包含其他资源(打开的文件,挂起的信号,内核内部数据,处理器状态,一个或多个具有内催音社的内存地址空间及一个或多个执行线 ...