信号处理——EMD、VMD的一点小思考

作者：桂。

时间：2017-03-06  20:57:22

链接：http://www.cnblogs.com/xingshansi/p/6511916.html

---

前言

本文为Hilbert变换一篇的内容补充，主要内容为：

　　1）EMD原理介绍

　　2）代码分析

　　3）一种权衡的小trick

　　4）问题补充

内容主要为自己的学习总结，并多有借鉴他人，最后一并给出链接。

一、EMD原理介绍

　　A-EMD的意义

很多人都知道EMD(Empirical Mode Decomposition)可以将信号分解不同频率特性，并且结合Hilbert求解包络以及瞬时频率。EMD、Hilbert、瞬时频率三者有无内在联系？答案是：有。

按照Hilbert变换一篇的介绍，

$f(t) = \frac{{d\Phi (t)}}{{d(t)}}$

然而，这样求解瞬时频率在某些情况下有问题，可能出现$f(t)$为负的情况：我1秒手指动5下，频率是5Hz；反过来，频率为8Hz时，手指1秒动8下，可如果频率为-5Hz呢？负频率没有意义。

考虑信号

$x(t) = {x_1}(t) + {x_2}(t) = {A_1}{e^{j{\omega _1}t}} + {A_2}{e^{j{\omega _2}t}} = A(t){e^{j\varphi (t)}}$

为了简单起见，假设$A_1$和$A_2$恒定，且$\omega_1$和$\omega_2$是正的。信号$x(t)$的频谱应由两个在$\omega_1$和$\omega_2$的$\delta$函数组成，即

$X(\omega ) = {A_1}\delta (\omega  - {\omega _1}) + {A_2}\delta (\omega  - {\omega _2})$

因为假设$\omega_1$和$\omega_2$是正的，所以该信号解析。求得相位

$\Phi (t) = \frac{{{A_1}\sin {\omega _1}t + {A_{\rm{2}}}\sin {\omega _{\rm{2}}}t}}{{{A_1}\cos {\omega _1}t + {A_{\rm{2}}}\cos {\omega _{\rm{2}}}t}}$

分别取两组参数，对$t$求导，得到对应参数下的瞬时频率：

参数：

$\omega_1 = 10Hz$和$\omega_2 = 20Hz$.

• 组1：{$A_1 = 0.2, A_2 = 1$};
• 组2：{$A_1 = 1.2, A_2 = 1$}

对于组2，瞬时频率出现了负值。

可见：

对任意信号进行Hilbert变换，可能出现无法解释、缺乏实际意义的频率分量。Norden E. Hung等人对瞬时频率进行研究后发现，只有满足特定条件的信号，其瞬时频率才具有物理意义，并将此类信号成为：IMF/基本模式分量。　

　　B-EMD基本原理

此处给一个原理图：

　　C-基本模式分量（IMF）

EMD分解的IMF其瞬时频率具有实际物理意义，原因有两点：

• 限定1：
  • 在整个数据序列中，极值点的数量$N_e$（包括极大值、极小值点）与过零点的数量必须相等，或最多相差1个，即$(N_e-1) \le N_e \ge (N_e+1)$.
• 限定2：
  • 在任意时间点$t_i$上，信号局部极大值确定的上包络线$f_{max}(t)$和局部极小值确定的下包络线$f_{min}(t)$的均值为0.

限定1即要求信号具有类似传统平稳高斯过程的分布；限定2要求局部均值为0，同时用局部最大、最小值的包络作为近似，从而信号局部对称，避免了不对称带来的瞬时频率波动。

　　D-VMD

关于VMD(Variational Mode Decomposition)，具体原理可以参考其论文，这里我们只要记住一点：其分解的各个基本分量——即各解析信号的瞬时频率具有实际的物理意义。

二、代码分析

首先给出信号分别用VMD、EMD的分解结果:

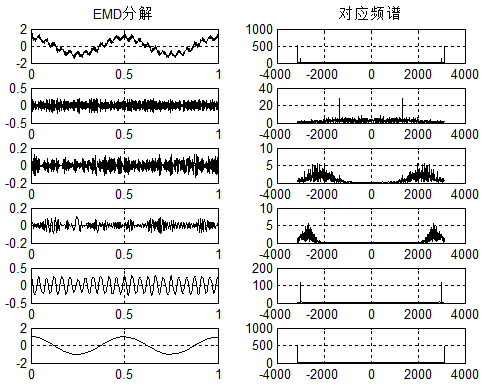
给出对应的代码：

%--------------- Preparation
clear all;
close all;
clc;
% Time Domain 0 to T
T = 1000;
fs = 1/T;
t = (1:T)/T;
freqs = 2*pi*(t-0.5-1/T)/(fs);
% center frequencies of components
f_1 = 2;
f_2 = 24;
f_3 = 288;
% modes
v_1 = (cos(2*pi*f_1*t));
v_2 = 1/4*(cos(2*pi*f_2*t));
v_3 = 1/16*(cos(2*pi*f_3*t));
% for visualization purposes
wsub{1} = 2*pi*f_1;
wsub{2} = 2*pi*f_2;
wsub{3} = 2*pi*f_3;
% composite signal, including noise
f = v_1 + v_2 + v_3 + 0.1*randn(size(v_1));
% some sample parameters for VMD
alpha = 2000;        % moderate bandwidth constraint
tau = 0;            % noise-tolerance (no strict fidelity enforcement)
K = 4;              % 4 modes
DC = 0;             % no DC part imposed
init = 1;           % initialize omegas uniformly
tol = 1e-7;

%--------------- Run actual VMD code
[u, u_hat, omega] = VMD(f, alpha, tau, K, DC, init, tol);
subplot(size(u,1)+1,2,1);
plot(t,f,'k');grid on;
title('VMD分解');
subplot(size(u,1)+1,2,2);
plot(freqs,abs(fft(f)),'k');grid on;
title('对应频谱');
for i = 2:size(u,1)+1
    subplot(size(u,1)+1,2,i*2-1);
    plot(t,u(i-1,:),'k');grid on;
    subplot(size(u,1)+1,2,i*2);
    plot(freqs,abs(fft(u(i-1,:))),'k');grid on;
end

%---------------run EMD code
imf = emd(f);
figure;
subplot(size(imf,1)+1,2,1);
plot(t,f,'k');grid on;
title('EMD分解');
subplot(size(imf,1)+1,2,2);
plot(freqs,abs(fft(f)),'k');grid on;
title('对应频谱');
for i = 2:size(imf,1)+1
    subplot(size(imf,1)+1,2,i*2-1);
    plot(t,imf(i-1,:),'k');grid on;
    subplot(size(imf,1)+1,2,i*2);
    plot(freqs,abs(fft(imf(i-1,:))),'k');grid on;
end

　　附上两个子程序的code.

VMD:

function [u, u_hat, omega] = VMD(signal, alpha, tau, K, DC, init, tol)
% Variational Mode Decomposition
% Authors: Konstantin Dragomiretskiy and Dominique Zosso
% zosso@math.ucla.edu --- http://www.math.ucla.edu/~zosso
% Initial release 2013-12-12 (c) 2013
%
% Input and Parameters:
% ---------------------
% signal  - the time domain signal (1D) to be decomposed
% alpha   - the balancing parameter of the data-fidelity constraint
% tau     - time-step of the dual ascent ( pick 0 for noise-slack )
% K       - the number of modes to be recovered
% DC      - true if the first mode is put and kept at DC (0-freq)
% init    - 0 = all omegas start at 0
%                    1 = all omegas start uniformly distributed
%                    2 = all omegas initialized randomly
% tol     - tolerance of convergence criterion; typically around 1e-6
%
% Output:
% -------
% u       - the collection of decomposed modes
% u_hat   - spectra of the modes
% omega   - estimated mode center-frequencies
%
% When using this code, please do cite our paper:
% -----------------------------------------------
% K. Dragomiretskiy, D. Zosso, Variational Mode Decomposition, IEEE Trans.
% on Signal Processing (in press)
% please check here for update reference:
%          http://dx.doi.org/10.1109/TSP.2013.2288675

%---------- Preparations

% Period and sampling frequency of input signal
save_T = length(signal);
fs = 1/save_T;

% extend the signal by mirroring
T = save_T;
f_mirror(1:T/2) = signal(T/2:-1:1);
f_mirror(T/2+1:3*T/2) = signal;
f_mirror(3*T/2+1:2*T) = signal(T:-1:T/2+1);
f = f_mirror;

% Time Domain 0 to T (of mirrored signal)
T = length(f);
t = (1:T)/T;

% Spectral Domain discretization
freqs = t-0.5-1/T;

% Maximum number of iterations (if not converged yet, then it won't anyway)
N = 500;

% For future generalizations: individual alpha for each mode
Alpha = alpha*ones(1,K);

% Construct and center f_hat
f_hat = fftshift((fft(f)));
f_hat_plus = f_hat;
f_hat_plus(1:T/2) = 0;

% matrix keeping track of every iterant // could be discarded for mem
u_hat_plus = zeros(N, length(freqs), K);

% Initialization of omega_k
omega_plus = zeros(N, K);
switch init
    case 1
        for i = 1:K
            omega_plus(1,i) = (0.5/K)*(i-1);
        end
    case 2
        omega_plus(1,:) = sort(exp(log(fs) + (log(0.5)-log(fs))*rand(1,K)));
    otherwise
        omega_plus(1,:) = 0;
end

% if DC mode imposed, set its omega to 0
if DC
    omega_plus(1,1) = 0;
end

% start with empty dual variables
lambda_hat = zeros(N, length(freqs));

% other inits
uDiff = tol+eps; % update step
n = 1; % loop counter
sum_uk = 0; % accumulator

% ----------- Main loop for iterative updates

while ( uDiff > tol &&  n < N ) % not converged and below iterations limit

    % update first mode accumulator
    k = 1;
    sum_uk = u_hat_plus(n,:,K) + sum_uk - u_hat_plus(n,:,1);

    % update spectrum of first mode through Wiener filter of residuals
    u_hat_plus(n+1,:,k) = (f_hat_plus - sum_uk - lambda_hat(n,:)/2)./(1+Alpha(1,k)*(freqs - omega_plus(n,k)).^2);

    % update first omega if not held at 0
    if ~DC
        omega_plus(n+1,k) = (freqs(T/2+1:T)*(abs(u_hat_plus(n+1, T/2+1:T, k)).^2)')/sum(abs(u_hat_plus(n+1,T/2+1:T,k)).^2);
    end

    % update of any other mode
    for k=2:K

        % accumulator
        sum_uk = u_hat_plus(n+1,:,k-1) + sum_uk - u_hat_plus(n,:,k);

        % mode spectrum
        u_hat_plus(n+1,:,k) = (f_hat_plus - sum_uk - lambda_hat(n,:)/2)./(1+Alpha(1,k)*(freqs - omega_plus(n,k)).^2);

        % center frequencies
        omega_plus(n+1,k) = (freqs(T/2+1:T)*(abs(u_hat_plus(n+1, T/2+1:T, k)).^2)')/sum(abs(u_hat_plus(n+1,T/2+1:T,k)).^2);

    end

    % Dual ascent
    lambda_hat(n+1,:) = lambda_hat(n,:) + tau*(sum(u_hat_plus(n+1,:,:),3) - f_hat_plus);

    % loop counter
    n = n+1;

    % converged yet?
    uDiff = eps;
    for i=1:K
        uDiff = uDiff + 1/T*(u_hat_plus(n,:,i)-u_hat_plus(n-1,:,i))*conj((u_hat_plus(n,:,i)-u_hat_plus(n-1,:,i)))';
    end
    uDiff = abs(uDiff);

end

%------ Postprocessing and cleanup

% discard empty space if converged early
N = min(N,n);
omega = omega_plus(1:N,:);

% Signal reconstruction
u_hat = zeros(T, K);
u_hat((T/2+1):T,:) = squeeze(u_hat_plus(N,(T/2+1):T,:));
u_hat((T/2+1):-1:2,:) = squeeze(conj(u_hat_plus(N,(T/2+1):T,:)));
u_hat(1,:) = conj(u_hat(end,:));

u = zeros(K,length(t));

for k = 1:K
    u(k,:)=real(ifft(ifftshift(u_hat(:,k))));
end

% remove mirror part
u = u(:,T/4+1:3*T/4);

% recompute spectrum
clear u_hat;
for k = 1:K
    u_hat(:,k)=fftshift(fft(u(k,:)))';
end

end

EMD:

%EMD  computes Empirical Mode Decomposition
%
%
%   Syntax
%
%
% IMF = EMD(X)
% IMF = EMD(X,...,'Option_name',Option_value,...)
% IMF = EMD(X,OPTS)
% [IMF,ORT,NB_ITERATIONS] = EMD(...)
%
%
%   Description
%
%
% IMF = EMD(X) where X is a real vector computes the Empirical Mode
% Decomposition [1] of X, resulting in a matrix IMF containing 1 IMF per row, the
% last one being the residue. The default stopping criterion is the one proposed
% in [2]:
%
%   at each point, mean_amplitude < THRESHOLD2*envelope_amplitude
%   &
%   mean of boolean array {(mean_amplitude)/(envelope_amplitude) > THRESHOLD} < TOLERANCE
%   &
%   |#zeros-#extrema|<=1
%
% where mean_amplitude = abs(envelope_max+envelope_min)/2
% and envelope_amplitude = abs(envelope_max-envelope_min)/2
%
% IMF = EMD(X) where X is a complex vector computes Bivariate Empirical Mode
% Decomposition [3] of X, resulting in a matrix IMF containing 1 IMF per row, the
% last one being the residue. The default stopping criterion is similar to the
% one proposed in [2]:
%
%   at each point, mean_amplitude < THRESHOLD2*envelope_amplitude
%   &
%   mean of boolean array {(mean_amplitude)/(envelope_amplitude) > THRESHOLD} < TOLERANCE
%
% where mean_amplitude and envelope_amplitude have definitions similar to the
% real case
%
% IMF = EMD(X,...,'Option_name',Option_value,...) sets options Option_name to
% the specified Option_value (see Options)
%
% IMF = EMD(X,OPTS) is equivalent to the above syntax provided OPTS is a struct
% object with field names corresponding to option names and field values being the
% associated values
%
% [IMF,ORT,NB_ITERATIONS] = EMD(...) returns an index of orthogonality
%                       ________
%         _  |IMF(i,:).*IMF(j,:)|
%   ORT = \ _____________________
%         /
%         ?       || X ||?%        i~=j
%
% and the number of iterations to extract each mode in NB_ITERATIONS
%
%
%   Options
%
%
%  stopping criterion options:
%
% STOP: vector of stopping parameters [THRESHOLD,THRESHOLD2,TOLERANCE]
% if the input vector's length is less than 3, only the first parameters are
% set, the remaining ones taking default values.
% default: [0.05,0.5,0.05]
%
% FIX (int): disable the default stopping criterion and do exactly <FIX>
% number of sifting iterations for each mode
%
% FIX_H (int): disable the default stopping criterion and do <FIX_H> sifting
% iterations with |#zeros-#extrema|<=1 to stop [4]
%
%  bivariate/complex EMD options:
%
% COMPLEX_VERSION: selects the algorithm used for complex EMD ([3])
% COMPLEX_VERSION = 1: "algorithm 1"
% COMPLEX_VERSION = 2: "algorithm 2" (default)
%
% NDIRS: number of directions in which envelopes are computed (default 4)
% rem: the actual number of directions (according to [3]) is 2*NDIRS
%
%  other options:
%
% T: sampling times (line vector) (default: 1:length(x))
%
% MAXITERATIONS: maximum number of sifting iterations for the computation of each
% mode (default: 2000)
%
% MAXMODES: maximum number of imfs extracted (default: Inf)
%
% DISPLAY: if equals to 1 shows sifting steps with pause
% if equals to 2 shows sifting steps without pause (movie style)
% rem: display is disabled when the input is complex
%
% INTERP: interpolation scheme: 'linear', 'cubic', 'pchip' or 'spline' (default)
% see interp1 documentation for details
%
% MASK: masking signal used to improve the decomposition according to [5]
%
%
%   Examples
%
%
%X = rand(1,512);
%
%IMF = emd(X);
%
%IMF = emd(X,'STOP',[0.1,0.5,0.05],'MAXITERATIONS',100);
%
%T=linspace(0,20,1e3);
%X = 2*exp(i*T)+exp(3*i*T)+.5*T;
%IMF = emd(X,'T',T);
%
%OPTIONS.DISLPAY = 1;
%OPTIONS.FIX = 10;
%OPTIONS.MAXMODES = 3;
%[IMF,ORT,NBITS] = emd(X,OPTIONS);
%
%
%   References
%
%
% [1] N. E. Huang et al., "The empirical mode decomposition and the
% Hilbert spectrum for non-linear and non stationary time series analysis",
% Proc. Royal Soc. London A, Vol. 454, pp. 903-995, 1998
%
% [2] G. Rilling, P. Flandrin and P. Gon鏰lves
% "On Empirical Mode Decomposition and its algorithms",
% IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing
% NSIP-03, Grado (I), June 2003
%
% [3] G. Rilling, P. Flandrin, P. Gon鏰lves and J. M. Lilly.,
% "Bivariate Empirical Mode Decomposition",
% Signal Processing Letters (submitted)
%
% [4] N. E. Huang et al., "A confidence limit for the Empirical Mode
% Decomposition and Hilbert spectral analysis",
% Proc. Royal Soc. London A, Vol. 459, pp. 2317-2345, 2003
%
% [5] R. Deering and J. F. Kaiser, "The use of a masking signal to improve
% empirical mode decomposition", ICASSP 2005
%
%
% See also
%  emd_visu (visualization),
%  emdc, emdc_fix (fast implementations of EMD),
%  cemdc, cemdc_fix, cemdc2, cemdc2_fix (fast implementations of bivariate EMD),
%  hhspectrum (Hilbert-Huang spectrum)
%
%
% G. Rilling, last modification: 3.2007
% gabriel.rilling@ens-lyon.fr

function [imf,ort,nbits] = emd(varargin)

[x,t,sd,sd2,tol,MODE_COMPLEX,ndirs,display_sifting,sdt,sd2t,r,imf,k,nbit,NbIt,MAXITERATIONS,FIXE,FIXE_H,MAXMODES,INTERP,mask] = init(varargin{:});

if display_sifting
  fig_h = figure;
end

%main loop : requires at least 3 extrema to proceed
while ~stop_EMD(r,MODE_COMPLEX,ndirs) && (k < MAXMODES+1 || MAXMODES == 0) && ~any(mask)

  % current mode
  m = r;

  % mode at previous iteration
  mp = m;

  %computation of mean and stopping criterion
  if FIXE
    [stop_sift,moyenne] = stop_sifting_fixe(t,m,INTERP,MODE_COMPLEX,ndirs);
  elseif FIXE_H
    stop_count = 0;
    [stop_sift,moyenne] = stop_sifting_fixe_h(t,m,INTERP,stop_count,FIXE_H,MODE_COMPLEX,ndirs);
  else
    [stop_sift,moyenne] = stop_sifting(m,t,sd,sd2,tol,INTERP,MODE_COMPLEX,ndirs);
  end

  % in case the current mode is so small that machine precision can cause
  % spurious extrema to appear
  if (max(abs(m))) < (1e-10)*(max(abs(x)))
    if ~stop_sift
      warning('emd:warning','forced stop of EMD : too small amplitude')
    else
      disp('forced stop of EMD : too small amplitude')
    end
    break
  end

  % sifting loop
  while ~stop_sift && nbit<MAXITERATIONS

    if(~MODE_COMPLEX && nbit>MAXITERATIONS/5 && mod(nbit,floor(MAXITERATIONS/10))==0 && ~FIXE && nbit > 100)
      disp(['mode ',int2str(k),', iteration ',int2str(nbit)])
      if exist('s','var')
        disp(['stop parameter mean value : ',num2str(s)])
      end
      [im,iM] = extr(m);
      disp([int2str(sum(m(im) > 0)),' minima > 0; ',int2str(sum(m(iM) < 0)),' maxima < 0.'])
    end

    %sifting
    m = m - moyenne;

    %computation of mean and stopping criterion
    if FIXE
      [stop_sift,moyenne] = stop_sifting_fixe(t,m,INTERP,MODE_COMPLEX,ndirs);
    elseif FIXE_H
      [stop_sift,moyenne,stop_count] = stop_sifting_fixe_h(t,m,INTERP,stop_count,FIXE_H,MODE_COMPLEX,ndirs);
    else
      [stop_sift,moyenne,s] = stop_sifting(m,t,sd,sd2,tol,INTERP,MODE_COMPLEX,ndirs);
    end

    % display
    if display_sifting && ~MODE_COMPLEX
      NBSYM = 2;
      [indmin,indmax] = extr(mp);
      [tmin,tmax,mmin,mmax] = boundary_conditions(indmin,indmax,t,mp,mp,NBSYM);
      envminp = interp1(tmin,mmin,t,INTERP);
      envmaxp = interp1(tmax,mmax,t,INTERP);
      envmoyp = (envminp+envmaxp)/2;
      if FIXE || FIXE_H
        display_emd_fixe(t,m,mp,r,envminp,envmaxp,envmoyp,nbit,k,display_sifting)
      else
        sxp=2*(abs(envmoyp))./(abs(envmaxp-envminp));
        sp = mean(sxp);
        display_emd(t,m,mp,r,envminp,envmaxp,envmoyp,s,sp,sxp,sdt,sd2t,nbit,k,display_sifting,stop_sift)
      end
    end

    mp = m;
    nbit=nbit+1;
    NbIt=NbIt+1;

    if(nbit==(MAXITERATIONS-1) && ~FIXE && nbit > 100)
      if exist('s','var')
        warning('emd:warning',['forced stop of sifting : too many iterations... mode ',int2str(k),'. stop parameter mean value : ',num2str(s)])
      else
        warning('emd:warning',['forced stop of sifting : too many iterations... mode ',int2str(k),'.'])
      end
    end

  end % sifting loop
  imf(k,:) = m;
  if display_sifting
    disp(['mode ',int2str(k),' stored'])
  end
  nbits(k) = nbit;
  k = k+1;

  r = r - m;
  nbit=0;

end %main loop

if any(r) && ~any(mask)
  imf(k,:) = r;
end

ort = io(x,imf);

if display_sifting
  close
end
end

%---------------------------------------------------------------------------------------------------
% tests if there are enough (3) extrema to continue the decomposition
function stop = stop_EMD(r,MODE_COMPLEX,ndirs)
if MODE_COMPLEX
  for k = 1:ndirs
    phi = (k-1)*pi/ndirs;
    [indmin,indmax] = extr(real(exp(i*phi)*r));
    ner(k) = length(indmin) + length(indmax);
  end
  stop = any(ner < 3);
else
  [indmin,indmax] = extr(r);
  ner = length(indmin) + length(indmax);
  stop = ner < 3;
end
end

%---------------------------------------------------------------------------------------------------
% computes the mean of the envelopes and the mode amplitude estimate
function [envmoy,nem,nzm,amp] = mean_and_amplitude(m,t,INTERP,MODE_COMPLEX,ndirs)
NBSYM = 2;
if MODE_COMPLEX
  switch MODE_COMPLEX
    case 1
      for k = 1:ndirs
        phi = (k-1)*pi/ndirs;
        y = real(exp(-i*phi)*m);
        [indmin,indmax,indzer] = extr(y);
        nem(k) = length(indmin)+length(indmax);
        nzm(k) = length(indzer);
        [tmin,tmax,zmin,zmax] = boundary_conditions(indmin,indmax,t,y,m,NBSYM);
        envmin(k,:) = interp1(tmin,zmin,t,INTERP);
        envmax(k,:) = interp1(tmax,zmax,t,INTERP);
      end
      envmoy = mean((envmin+envmax)/2,1);
      if nargout > 3
        amp = mean(abs(envmax-envmin),1)/2;
      end
    case 2
      for k = 1:ndirs
        phi = (k-1)*pi/ndirs;
        y = real(exp(-i*phi)*m);
        [indmin,indmax,indzer] = extr(y);
        nem(k) = length(indmin)+length(indmax);
        nzm(k) = length(indzer);
        [tmin,tmax,zmin,zmax] = boundary_conditions(indmin,indmax,t,y,y,NBSYM);
        envmin(k,:) = exp(i*phi)*interp1(tmin,zmin,t,INTERP);
        envmax(k,:) = exp(i*phi)*interp1(tmax,zmax,t,INTERP);
      end
      envmoy = mean((envmin+envmax),1);
      if nargout > 3
        amp = mean(abs(envmax-envmin),1)/2;
      end
  end
else
  [indmin,indmax,indzer] = extr(m);
  nem = length(indmin)+length(indmax);
  nzm = length(indzer);
  [tmin,tmax,mmin,mmax] = boundary_conditions(indmin,indmax,t,m,m,NBSYM);
  envmin = interp1(tmin,mmin,t,INTERP);
  envmax = interp1(tmax,mmax,t,INTERP);
  envmoy = (envmin+envmax)/2;
  if nargout > 3
    amp = mean(abs(envmax-envmin),1)/2;
  end
end
end

%-------------------------------------------------------------------------------
% default stopping criterion
function [stop,envmoy,s] = stop_sifting(m,t,sd,sd2,tol,INTERP,MODE_COMPLEX,ndirs)
try
  [envmoy,nem,nzm,amp] = mean_and_amplitude(m,t,INTERP,MODE_COMPLEX,ndirs);
  sx = abs(envmoy)./amp;
  s = mean(sx);
  stop = ~((mean(sx > sd) > tol | any(sx > sd2)) & (all(nem > 2)));
  if ~MODE_COMPLEX
    stop = stop && ~(abs(nzm-nem)>1);
  end
catch
  stop = 1;
  envmoy = zeros(1,length(m));
  s = NaN;
end
end

%-------------------------------------------------------------------------------
% stopping criterion corresponding to option FIX
function [stop,moyenne]= stop_sifting_fixe(t,m,INTERP,MODE_COMPLEX,ndirs)
try
  moyenne = mean_and_amplitude(m,t,INTERP,MODE_COMPLEX,ndirs);
  stop = 0;
catch
  moyenne = zeros(1,length(m));
  stop = 1;
end
end

%-------------------------------------------------------------------------------
% stopping criterion corresponding to option FIX_H
function [stop,moyenne,stop_count]= stop_sifting_fixe_h(t,m,INTERP,stop_count,FIXE_H,MODE_COMPLEX,ndirs)
try
  [moyenne,nem,nzm] = mean_and_amplitude(m,t,INTERP,MODE_COMPLEX,ndirs);
  if (all(abs(nzm-nem)>1))
    stop = 0;
    stop_count = 0;
  else
    stop_count = stop_count+1;
    stop = (stop_count == FIXE_H);
  end
catch
  moyenne = zeros(1,length(m));
  stop = 1;
end
end

%-------------------------------------------------------------------------------
% displays the progression of the decomposition with the default stopping criterion
function display_emd(t,m,mp,r,envmin,envmax,envmoy,s,sb,sx,sdt,sd2t,nbit,k,display_sifting,stop_sift)
subplot(4,1,1)
plot(t,mp);hold on;
plot(t,envmax,'--k');plot(t,envmin,'--k');plot(t,envmoy,'r');
title(['IMF ',int2str(k),';   iteration ',int2str(nbit),' before sifting']);
set(gca,'XTick',[])
hold  off
subplot(4,1,2)
plot(t,sx)
hold on
plot(t,sdt,'--r')
plot(t,sd2t,':k')
title('stop parameter')
set(gca,'XTick',[])
hold off
subplot(4,1,3)
plot(t,m)
title(['IMF ',int2str(k),';   iteration ',int2str(nbit),' after sifting']);
set(gca,'XTick',[])
subplot(4,1,4);
plot(t,r-m)
title('residue');
disp(['stop parameter mean value : ',num2str(sb),' before sifting and ',num2str(s),' after'])
if stop_sift
  disp('last iteration for this mode')
end
if display_sifting == 2
  pause(0.01)
else
  pause
end
end

%---------------------------------------------------------------------------------------------------
% displays the progression of the decomposition with the FIX and FIX_H stopping criteria
function display_emd_fixe(t,m,mp,r,envmin,envmax,envmoy,nbit,k,display_sifting)
subplot(3,1,1)
plot(t,mp);hold on;
plot(t,envmax,'--k');plot(t,envmin,'--k');plot(t,envmoy,'r');
title(['IMF ',int2str(k),';   iteration ',int2str(nbit),' before sifting']);
set(gca,'XTick',[])
hold  off
subplot(3,1,2)
plot(t,m)
title(['IMF ',int2str(k),';   iteration ',int2str(nbit),' after sifting']);
set(gca,'XTick',[])
subplot(3,1,3);
plot(t,r-m)
title('residue');
if display_sifting == 2
  pause(0.01)
else
  pause
end
end

%---------------------------------------------------------------------------------------
% defines new extrema points to extend the interpolations at the edges of the
% signal (mainly mirror symmetry)
function [tmin,tmax,zmin,zmax] = boundary_conditions(indmin,indmax,t,x,z,nbsym)

	lx = length(x);

	if (length(indmin) + length(indmax) < 3)
		error('not enough extrema')
	end

    % boundary conditions for interpolations :

	if indmax(1) < indmin(1)
    	if x(1) > x(indmin(1))
			lmax = fliplr(indmax(2:min(end,nbsym+1)));
			lmin = fliplr(indmin(1:min(end,nbsym)));
			lsym = indmax(1);
		else
			lmax = fliplr(indmax(1:min(end,nbsym)));
			lmin = [fliplr(indmin(1:min(end,nbsym-1))),1];
			lsym = 1;
		end
	else

		if x(1) < x(indmax(1))
			lmax = fliplr(indmax(1:min(end,nbsym)));
			lmin = fliplr(indmin(2:min(end,nbsym+1)));
			lsym = indmin(1);
		else
			lmax = [fliplr(indmax(1:min(end,nbsym-1))),1];
			lmin = fliplr(indmin(1:min(end,nbsym)));
			lsym = 1;
		end
	end

	if indmax(end) < indmin(end)
		if x(end) < x(indmax(end))
			rmax = fliplr(indmax(max(end-nbsym+1,1):end));
			rmin = fliplr(indmin(max(end-nbsym,1):end-1));
			rsym = indmin(end);
		else
			rmax = [lx,fliplr(indmax(max(end-nbsym+2,1):end))];
			rmin = fliplr(indmin(max(end-nbsym+1,1):end));
			rsym = lx;
		end
	else
		if x(end) > x(indmin(end))
			rmax = fliplr(indmax(max(end-nbsym,1):end-1));
			rmin = fliplr(indmin(max(end-nbsym+1,1):end));
			rsym = indmax(end);
		else
			rmax = fliplr(indmax(max(end-nbsym+1,1):end));
			rmin = [lx,fliplr(indmin(max(end-nbsym+2,1):end))];
			rsym = lx;
		end
	end

	tlmin = 2*t(lsym)-t(lmin);
	tlmax = 2*t(lsym)-t(lmax);
	trmin = 2*t(rsym)-t(rmin);
	trmax = 2*t(rsym)-t(rmax);

	% in case symmetrized parts do not extend enough
	if tlmin(1) > t(1) || tlmax(1) > t(1)
		if lsym == indmax(1)
			lmax = fliplr(indmax(1:min(end,nbsym)));
		else
			lmin = fliplr(indmin(1:min(end,nbsym)));
		end
		if lsym == 1
			error('bug')
		end
		lsym = 1;
		tlmin = 2*t(lsym)-t(lmin);
		tlmax = 2*t(lsym)-t(lmax);
	end   

	if trmin(end) < t(lx) || trmax(end) < t(lx)
		if rsym == indmax(end)
			rmax = fliplr(indmax(max(end-nbsym+1,1):end));
		else
			rmin = fliplr(indmin(max(end-nbsym+1,1):end));
		end
	if rsym == lx
		error('bug')
	end
		rsym = lx;
		trmin = 2*t(rsym)-t(rmin);
		trmax = 2*t(rsym)-t(rmax);
	end 

	zlmax =z(lmax);
	zlmin =z(lmin);
	zrmax =z(rmax);
	zrmin =z(rmin);

	tmin = [tlmin t(indmin) trmin];
	tmax = [tlmax t(indmax) trmax];
	zmin = [zlmin z(indmin) zrmin];
	zmax = [zlmax z(indmax) zrmax];
end

%---------------------------------------------------------------------------------------------------
%extracts the indices of extrema
function [indmin, indmax, indzer] = extr(x,t)

if(nargin==1)
  t=1:length(x);
end

m = length(x);

if nargout > 2
  x1=x(1:m-1);
  x2=x(2:m);
  indzer = find(x1.*x2<0);

  if any(x == 0)
    iz = find( x==0 );
    indz = [];
    if any(diff(iz)==1)
      zer = x == 0;
      dz = diff([0 zer 0]);
      debz = find(dz == 1);
      finz = find(dz == -1)-1;
      indz = round((debz+finz)/2);
    else
      indz = iz;
    end
    indzer = sort([indzer indz]);
  end
end

d = diff(x);

n = length(d);
d1 = d(1:n-1);
d2 = d(2:n);
indmin = find(d1.*d2<0 & d1<0)+1;
indmax = find(d1.*d2<0 & d1>0)+1;

% when two or more successive points have the same value we consider only one extremum in the middle of the constant area
% (only works if the signal is uniformly sampled)

if any(d==0)

  imax = [];
  imin = [];

  bad = (d==0);
  dd = diff([0 bad 0]);
  debs = find(dd == 1);
  fins = find(dd == -1);
  if debs(1) == 1
    if length(debs) > 1
      debs = debs(2:end);
      fins = fins(2:end);
    else
      debs = [];
      fins = [];
    end
  end
  if length(debs) > 0
    if fins(end) == m
      if length(debs) > 1
        debs = debs(1:(end-1));
        fins = fins(1:(end-1));

      else
        debs = [];
        fins = [];
      end
    end
  end
  lc = length(debs);
  if lc > 0
    for k = 1:lc
      if d(debs(k)-1) > 0
        if d(fins(k)) < 0
          imax = [imax round((fins(k)+debs(k))/2)];
        end
      else
        if d(fins(k)) > 0
          imin = [imin round((fins(k)+debs(k))/2)];
        end
      end
    end
  end

  if length(imax) > 0
    indmax = sort([indmax imax]);
  end

  if length(imin) > 0
    indmin = sort([indmin imin]);
  end

end
end

%---------------------------------------------------------------------------------------------------

function ort = io(x,imf)
% ort = IO(x,imf) computes the index of orthogonality
%
% inputs : - x    : analyzed signal
%          - imf  : empirical mode decomposition

n = size(imf,1);

s = 0;

for i = 1:n
  for j =1:n
    if i~=j
      s = s + abs(sum(imf(i,:).*conj(imf(j,:)))/sum(x.^2));
    end
  end
end

ort = 0.5*s;
end
%---------------------------------------------------------------------------------------------------

function [x,t,sd,sd2,tol,MODE_COMPLEX,ndirs,display_sifting,sdt,sd2t,r,imf,k,nbit,NbIt,MAXITERATIONS,FIXE,FIXE_H,MAXMODES,INTERP,mask] = init(varargin)

x = varargin{1};
if nargin == 2
  if isstruct(varargin{2})
    inopts = varargin{2};
  else
    error('when using 2 arguments the first one is the analyzed signal X and the second one is a struct object describing the options')
  end
elseif nargin > 2
  try
    inopts = struct(varargin{2:end});
  catch
    error('bad argument syntax')
  end
end

% default for stopping
defstop = [0.05,0.5,0.05];

opt_fields = {'t','stop','display','maxiterations','fix','maxmodes','interp','fix_h','mask','ndirs','complex_version'};

defopts.stop = defstop;
defopts.display = 0;
defopts.t = 1:max(size(x));
defopts.maxiterations = 2000;
defopts.fix = 0;
defopts.maxmodes = 0;
defopts.interp = 'spline';
defopts.fix_h = 0;
defopts.mask = 0;
defopts.ndirs = 4;
defopts.complex_version = 2;

opts = defopts;

if(nargin==1)
  inopts = defopts;
elseif nargin == 0
  error('not enough arguments')
end

names = fieldnames(inopts);
for nom = names'
  if ~any(strcmpi(char(nom), opt_fields))
    error(['bad option field name: ',char(nom)])
  end
  if ~isempty(eval(['inopts.',char(nom)])) % empty values are discarded
    eval(['opts.',lower(char(nom)),' = inopts.',char(nom),';'])
  end
end

t = opts.t;
stop = opts.stop;
display_sifting = opts.display;
MAXITERATIONS = opts.maxiterations;
FIXE = opts.fix;
MAXMODES = opts.maxmodes;
INTERP = opts.interp;
FIXE_H = opts.fix_h;
mask = opts.mask;
ndirs = opts.ndirs;
complex_version = opts.complex_version;

if ~isvector(x)
  error('X must have only one row or one column')
end

if size(x,1) > 1
  x = x.';
end

if ~isvector(t)
  error('option field T must have only one row or one column')
end

if ~isreal(t)
  error('time instants T must be a real vector')
end

if size(t,1) > 1
  t = t';
end

if (length(t)~=length(x))
  error('X and option field T must have the same length')
end

if ~isvector(stop) || length(stop) > 3
  error('option field STOP must have only one row or one column of max three elements')
end

if ~all(isfinite(x))
  error('data elements must be finite')
end

if size(stop,1) > 1
  stop = stop';
end

L = length(stop);
if L < 3
  stop(3)=defstop(3);
end

if L < 2
  stop(2)=defstop(2);
end

if ~ischar(INTERP) || ~any(strcmpi(INTERP,{'linear','cubic','spline'}))
  error('INTERP field must be ''linear'', ''cubic'', ''pchip'' or ''spline''')
end

%special procedure when a masking signal is specified
if any(mask)
  if ~isvector(mask) || length(mask) ~= length(x)
    error('masking signal must have the same dimension as the analyzed signal X')
  end

  if size(mask,1) > 1
    mask = mask.';
  end
  opts.mask = 0;
  imf1 = emd(x+mask,opts);
  imf2 = emd(x-mask,opts);
  if size(imf1,1) ~= size(imf2,1)
    warning('emd:warning',['the two sets of IMFs have different sizes: ',int2str(size(imf1,1)),' and ',int2str(size(imf2,1)),' IMFs.'])
  end
  S1 = size(imf1,1);
  S2 = size(imf2,1);
  if S1 ~= S2
    if S1 < S2
      tmp = imf1;
      imf1 = imf2;
      imf2 = tmp;
    end
    imf2(max(S1,S2),1) = 0;
  end
  imf = (imf1+imf2)/2;

end

sd = stop(1);
sd2 = stop(2);
tol = stop(3);

lx = length(x);

sdt = sd*ones(1,lx);
sd2t = sd2*ones(1,lx);

if FIXE
  MAXITERATIONS = FIXE;
  if FIXE_H
    error('cannot use both ''FIX'' and ''FIX_H'' modes')
  end
end

MODE_COMPLEX = ~isreal(x)*complex_version;
if MODE_COMPLEX && complex_version ~= 1 && complex_version ~= 2
  error('COMPLEX_VERSION parameter must equal 1 or 2')
end

% number of extrema and zero-crossings in residual
ner = lx;
nzr = lx;

r = x;

if ~any(mask) % if a masking signal is specified "imf" already exists at this stage
  imf = [];
end
k = 1;

% iterations counter for extraction of 1 mode
nbit=0;

% total iterations counter
NbIt=0;
end
%---------------------------------------------------------------------------------------------------

关于EMD，有对应的工具箱。VMD也有扩展的二维分解，此处不再展开。

三、一种权衡的小trick

关于瞬时频率的原理以及代码，参考另一篇博文。

比较来看：

• EMD分解的IMF分量个数不能人为设定，而VMD(Variational Mode Decomposition)则可以;
• 但VMD也有弊端：分解过多，则信号断断续续，没有多少规律可言。

能不能取长补短呢？

自己之前做了一个小code，放在这里，供大家交流使用（此理论为自己首创，版权所有，拿去也不介意！(●'◡'●)）。
给定一个信号,下图是EMD分解结果，分解出了5个分量。

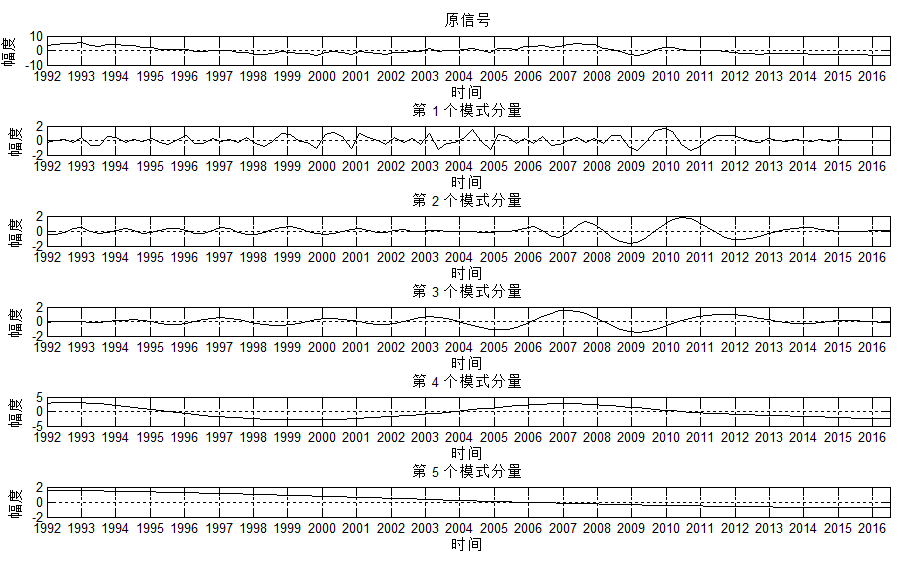
再来一个VMD（设定分量个数为3）的分解结果：

比较两个结果，可以发现：VMD的低频分量，更容易表达出经济波动的大趋势，而EMD则不易观察该特性。
或许有人会说：几个EMD分量叠加一下，也会有该效果，但如果不观察分解的数据，如何确定几个分量相加呢？更何况EMD总的IMF个数也是未知！

VMD的优势观察到了，但如何确定分量个数呢？
再来一个效果图：

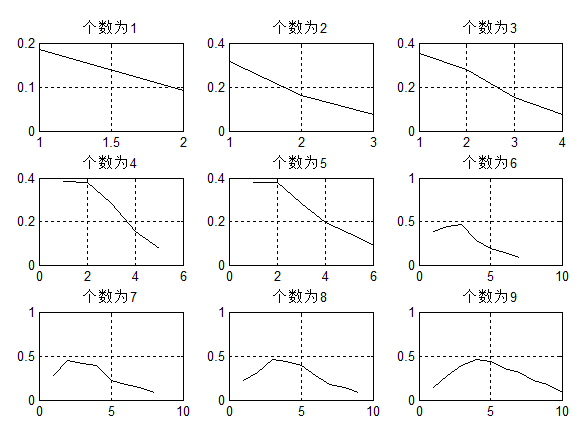
这里分析了VMD分量从1~9，9种情况下某特征的曲线，可以观察到：个数增加到一定数量，曲线有了明显的下弯曲现象（该特性容易借助曲率，进行量化分析，不再展开），这个临界的个数就是分解的合适数量，此处：K=3，因为到4就有了明显的下弯曲。

可见通过该特征，即可理论上得出最优K。下面讲一讲这个某特征为何物？
上一段代码：

for st=1:9
    K=st+1;
    [u, u_hat, omega] = VMD(data, length(data), 0, K, 0, 1, 1e-5);
    u=flipud(u);
    resf=zeros(1,K);
    for i=1:K
        testdata=u(i,:);
        hilbert(testdata');
        z=hilbert(testdata');                   % 希尔伯特变换
        a=abs(z);                               % 包络线
        fnor=instfreq(z);                       % 瞬时频率
        resf(i)=mean(fnor);
    end
    subplot(3,3,st)
    plot(resf,'k');title(['个数为',num2str(st)]);grid on;
end

　　没错，该特征就是：分量瞬时频率的均值。如果分解个数过大，则分量会出现断断絮絮地现象，特别是在高频，这样一来，即使是高频，平均瞬时频率反而低一些，这也是下弯曲的根本原因。

这个小trick就介绍到这里。

四、问题补充

HHT算法中，有两处存在端点效应，VMD是否也有呢？这一点没有再去验证。另外，关于Hilbert的端点效应，在另一篇博文已经给出。

参考：

宋知用：《MATLAB在语音信号分析和合成中的应用》

了凡春秋： http://blog.sina.com.cn/s/blog_6163bdeb0102e2cd.html

VMD-code:https://cn.mathworks.com/matlabcentral/fileexchange/44765-variational-mode-decomposition

EMD原理图：http://blog.sciencenet.cn/blog-244606-256958.html