剑指Offer 31. 整数中1出现的次数（从1到n整数中1出现的次数） （其他）

题目描述

求出1~13的整数中1出现的次数,并算出100~1300的整数中1出现的次数？为此他特别数了一下1~13中包含1的数字有1、10、11、12、13因此共出现6次,但是对于后面问题他就没辙了。ACMer希望你们帮帮他,并把问题更加普遍化,可以很快的求出任意非负整数区间中1出现的次数（从1 到 n 中1出现的次数）。

题目地址

https://www.nowcoder.com/practice/bd7f978302044eee894445e244c7eee6?tpId=13&tqId=11184&tPage=2&rp=2&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking

思路

思路1

从1到n遍历。对每一个数字，每次通过对10求余数判断整数的个位数字是不是1，大于10的除以10之后再判断，我们对每个数字都要做求余和除法运算以求出该数字中1出现的次数。如果输入数字n，n有O(logn)位，我们需要判断每一位是不是1，那么时间复杂度为O(n*logn)。

思路2

考虑将n的十进制的每一位单独拿出讨论，每一位的值记为weight。

1) 个位

从1到n，每增加1，weight就会加1，当weight加到9时，再加1又会回到0重新开始。那么weight从0-9的这种周期会出现多少次呢？这取决于n的高位是多少，看图：

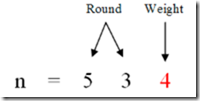
以534为例，在从1增长到n的过程中，534的个位从0-9变化了53次，记为round。每一轮变化中，1在个位出现一次，所以一共出现了53次。

再来看weight的值。weight为4，大于0，说明第54轮变化是从0-4，1又出现了1次。我们记1出现的次数为count，所以：

count = round+1 = 53 + 1 = 54

如果此时weight为0（n=530），说明第54轮到0就停止了，那么：

count = round = 53

2) 十位

对于10位来说，其0-9周期的出现次数与个位的统计方式是相同的，见图：

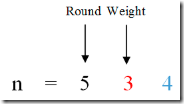
不同点在于：从1到n，每增加10，十位的weight才会增加1，所以，一轮0-9周期内，1会出现10次。即rount*10。

再来看weight的值。当此时weight为3，大于1，说明第6轮出现了10次1，则：

count = round*10+10 = 5*10+10 = 60

如果此时weight的值等于0（n=504），说明第6轮到0就停止了，所以：

count = round*10+10 = 5*10 = 50

如果此时weight的值等于1（n=514），那么第6轮中1出现了多少次呢？很明显，这与个位数的值有关，个位数为k，第6轮中1就出现了k+1次(0-k)。我们记个位数为former，则：

count = round*10+former +1= 5*10+4 = 55

3) 更高位

更高位的计算方式其实与十位是一致的，不再阐述。

4) 总结

将n的各个位分为两类：个位与其它位。

对个位来说：

• 若个位大于0，1出现的次数为round*1+1
• 若个位等于0，1出现的次数为round*1

对其它位来说，记每一位的权值为base，位值为weight，该位之前的数是former，举例如图：

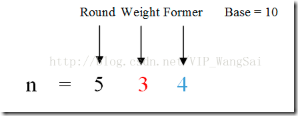
则：

• 若weight为0，则1出现次数为round*base
• 若weight为1，则1出现次数为round*base+former+1
• 若weight大于1，则1出现次数为rount*base+base

比如：

• 534 = （个位1出现次数）+（十位1出现次数）+（百位1出现次数）=（53*1+1）+（5*10+10）+（0*100+100）= 214
• 530 = （53*1）+（5*10+10）+（0*100+100） = 213
• 504 = （50*1+1）+（5*10）+（0*100+100） = 201
• 514 = （51*1+1）+（5*10+4+1）+（0*100+100） = 207
• 10 = (1*1)+(0*10+0+1) = 2

Python

# -*- coding:utf-8 -*-
class Solution:
    def NumberOf1Between1AndN_Solution(self, n):
        # write code here
        # res = 0
        # for i in range(1,n+1):
        #     while i:
        #         if i%10 == 1:
        #             res += 1
        #         i //= 10
        # return res
        # 思路2
        if n < 1:
            return 0
        count, base, Round = 0,1,n
        while Round > 0:
            weight = Round%10
            Round //= 10
            count += Round*base
            if weight == 1:
                count += n%base+1
            elif weight>1:
                count += base
            base *= 10
        return count

if __name__ == '__main__':
    result = Solution().NumberOf1Between1AndN_Solution(13)
    print(result)

参考

https://blog.csdn.net/yi_afly/article/details/52012593