Scala进阶之路-尾递归优化

　　　　　　　　　　　　　　Scala进阶之路-尾递归优化

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　作者：尹正杰

版权声明：原创作品，谢绝转载！否则将追究法律责任。

　　递归调用有时候能被转换成循环，这样能节约栈空间。在函数式编程中，这是很重要的，我们通常会使用递归方法来遍历集合。而不是所有的递归都能被优化。递归之所有能被优化是在指在函数的最后一行为递归调用（即尾递归），并且这个递归调用没有其它元素参与。

一.什么情况能导致栈的溢出

1>.循环调用

　　答：循环调用并不会导致栈的溢出，因为循环是一个压栈和弹栈的过程。

2>.递归调用

　　答：递归调用会导致栈的溢出。因为递归调用一直在压栈，而之前的栈并不会释放资源，这样随着压栈的堆积，栈空间溢出那是迟早的事儿。

3>.尾递归

　　答：可以进行优化，将递归转换成循环实现，避免栈的溢出。

二.尾递归优化案例展示

1>尾递归不能有其它参数参与

　　我们先以下案例：

 /*
 @author :yinzhengjie
 Blog:http://www.cnblogs.com/yinzhengjie/tag/Scala%E8%BF%9B%E9%98%B6%E4%B9%8B%E8%B7%AF/
 EMAIL:y1053419035@qq.com
 */
 package cn.org.yinzhengjie.function

 object TailRecursion {
     //定义递归函数
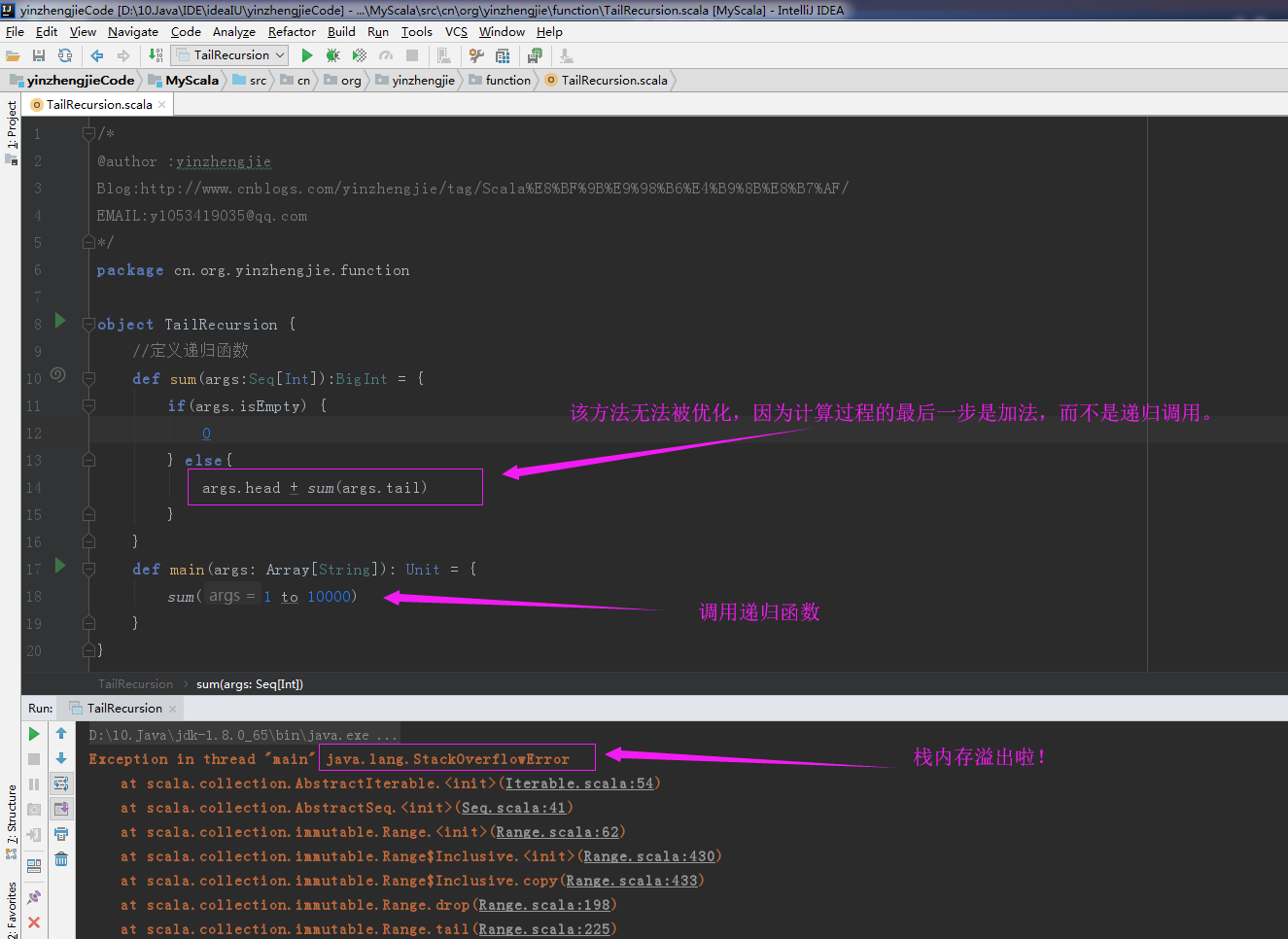
     def sum(args:Seq[Int]):BigInt = {
         if(args.isEmpty) {
             0
         } else{
             args.head + sum(args.tail)
         }
     }
     def main(args: Array[String]): Unit = {
         sum(1 to 10000)
     }
 }

　　以上代码测试结果如下:

2>.尾递归优化

　　我们将上面的代码稍微进行改动，就可以轻松实现尾递归优化啦。具体代码如下：

 /*
 @author :yinzhengjie
 Blog:http://www.cnblogs.com/yinzhengjie/tag/Scala%E8%BF%9B%E9%98%B6%E4%B9%8B%E8%B7%AF/
 EMAIL:y1053419035@qq.com
 */
 package cn.org.yinzhengjie.function

 object TailRecursion {
     //定义尾递归函数
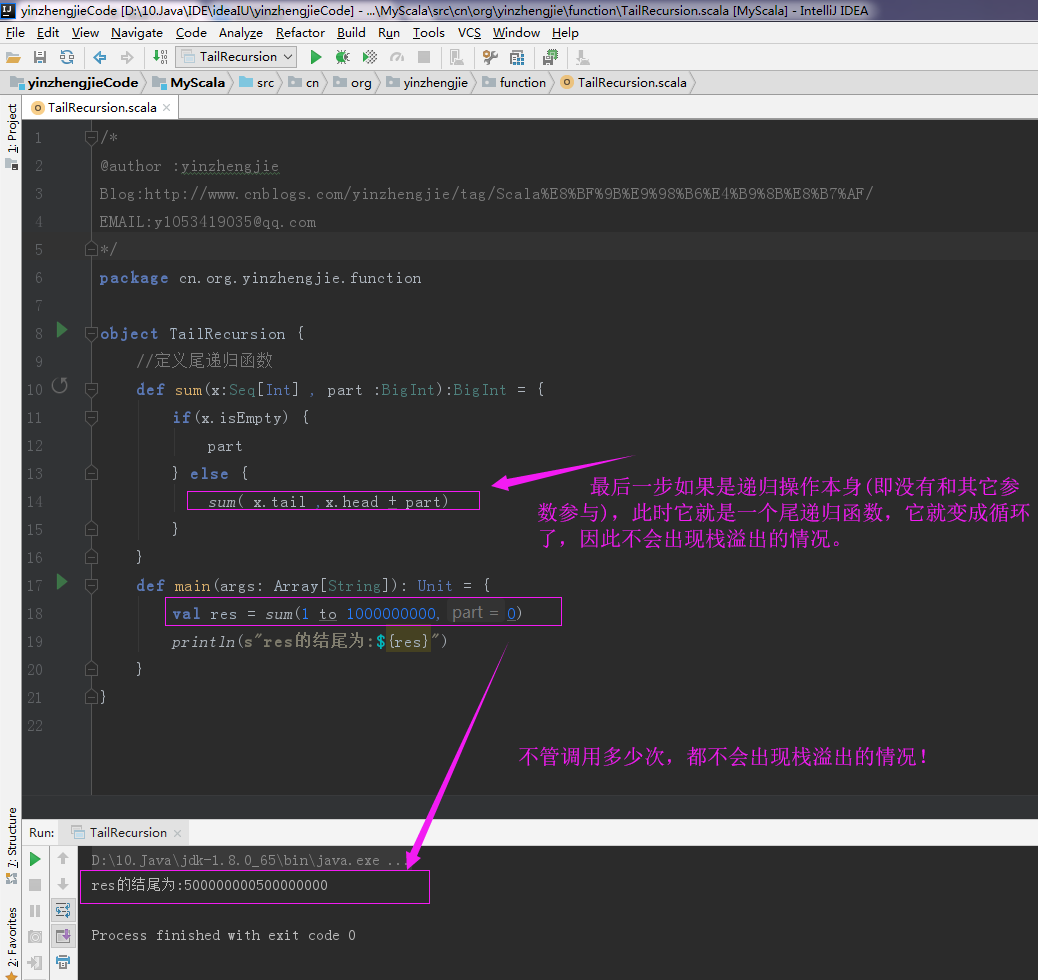
     def sum(x:Seq[Int] , part :BigInt):BigInt = {
         if(x.isEmpty) {
             part
         } else {
             sum( x.tail ,x.head + part)
         }
     }
     def main(args: Array[String]): Unit = {
         val res = sum(1 to 1000000000,0)
         println(s"res的结尾为:${res}")
     }
 }

　　测试结果如下：

三.如果编写尾递归函数

　　所谓的尾递归就是最后一步如果是递归操作本身(即没有和其它参数参与)，此时它就是一个尾递归函数，它就变成循环了，因此不会出现栈溢出的情况。能实现尾递归的原理就是当然的栈并不需要从下一个栈中拿数据才能释放。也就是说，当前的栈调用下一个栈时不依赖下一个栈返回数据才能结束，因此当它调用下一个栈时，也就可以让当前的栈执行弹栈操作，当下一个栈执行完毕时，也不需要下下个栈返回数据，因此，下一个栈也可以实现弹栈操作，综上所述，尾递归的就和咱们写的死循环是一个原理啦，就是实现压栈和弹栈的过程，因此始终不会栈溢出的情况哟！

　　我们再举一个尾递归的例子如下：

 /*
 @author :yinzhengjie
 Blog:http://www.cnblogs.com/yinzhengjie/tag/Scala%E8%BF%9B%E9%98%B6%E4%B9%8B%E8%B7%AF/
 EMAIL:y1053419035@qq.com
 */
 package cn.org.yinzhengjie.function

 object TailRecursion {
     //定义尾递归函数
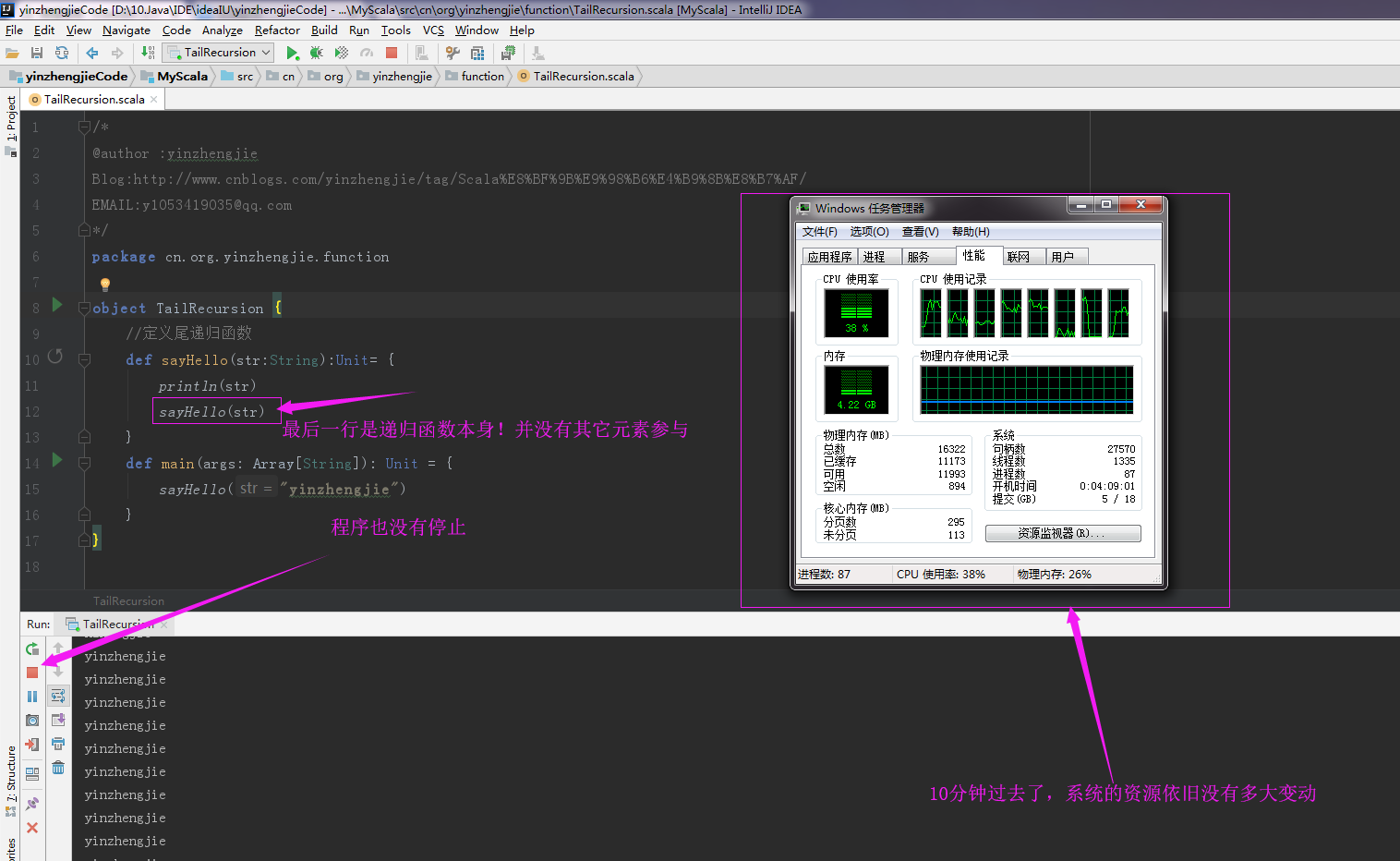
     def sayHello(str:String):Unit= {
         println(str)
         sayHello(str)
     }
     def main(args: Array[String]): Unit = {
         sayHello("yinzhengjie")
     }
 }

　　以上程序我执行了5分钟，依旧没有出现栈溢出的情况，

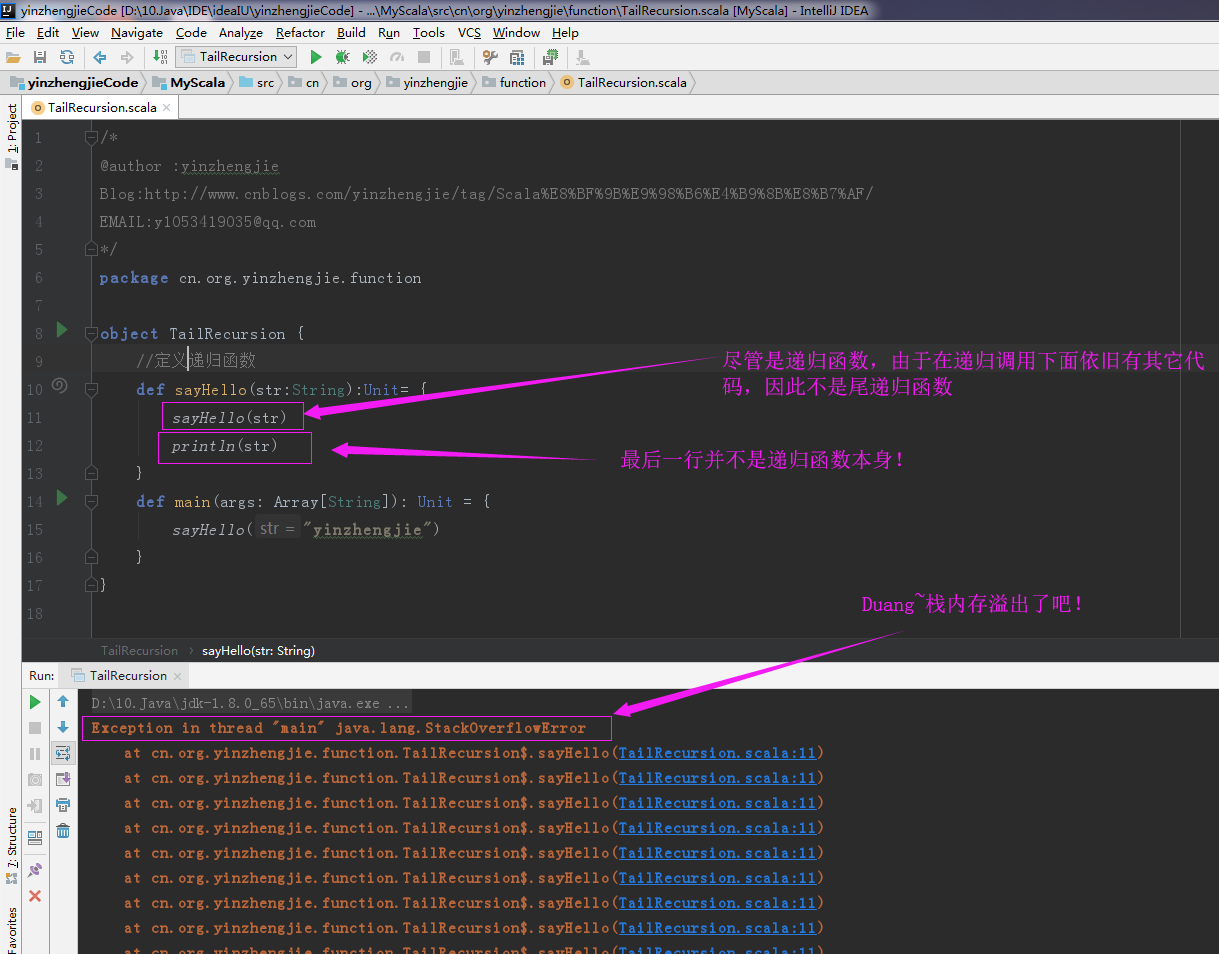
　　当然如果是你讲上面的尾递归函数的两行代码调换一下，当然依旧还是递归函数，但最后一行不是递归函数本身了，因此不是尾递归函数，很显然会出现栈内存溢出。