整数划分问题（记忆化搜索和DP方法）

一、 问题 现在有一正整数N，要把它分为若干正整数之和，问有多少种本质不同的分法？

（1）其中最大数不超过m, 有多少种分法？

（2）分割后的正整数的数目不超过m个， 有多少种分法？

（3）分成最大数不超过m， 且每一个正整数都是正奇数， 有多少种分法？

（4）分成最大数不超过m， 且每一个正整数都不同，有多少种分法？

（5）分成恰好k个正整数，有多少种分法？

二、分析

（1）最大数不超过 m

　　（a）设dp[i][j]表示把数字 i 分成最大数不超过  j 的若干正整数之和所得的方法数

　　（b）有如下递推公式 ，核心是最大数m到底选还是不选

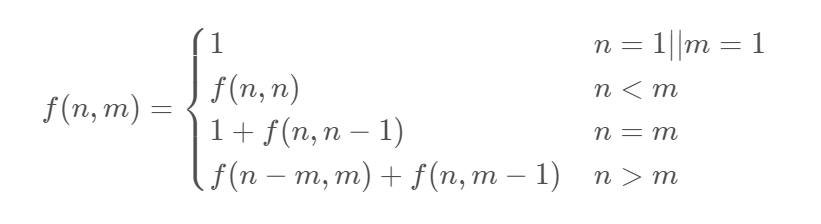
（2）分割数不超过m个

　　（a）设dp[i][j] 表示把数字 i 分成分割数不超过 j 的若干正整数之和所得的方法数

　　（b）递推公式核心：

• 到底分不分成 j 个
  • 　　如果分成j个，则预先给每一份分 一个1，那么还剩下n-m，这n-m仍然继续分割成最多j个数；
  • 　　如果不分成j个，那就转移到了把 i 最多分成 j-1 个数的状态
• 递推公式：

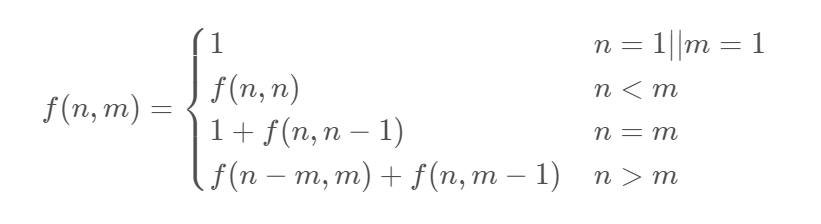
• 发现竟然和（1）完全一样！其实（1）（2）问题是完全等价的
  • 　　从递推公式上来看，等价
  • 　　从图形来看等价：

（3）分成最大数不超过m， 且每一个数都是正奇数

　　（a）设dp[i][j] 表示把数字 i 分成分割数不超过 j 的若干正奇数之和所得的方法数

　　（b）递推公式核心： 最大数 j 到底是不是奇数

• 如果是奇数，那么 j 是可以作为 一种分法的元素的 转态转移到到底是分出 j 还是不分出 j
• 如果不是奇数， 那么 j 是不能分出来的，状态转移到了dp[i][j-1]

（4）分成最大数不超过m， 且每一个正整数都不同

　　（a）设dp[i][j] 表示把数字 i 分成最大数不超过 j 的若干不同正整数之和所得的方法数

　　（b）递推公式核心：当前最大数选还是不选，如果选，还剩下i-j并且下次的最大数不能再是j而是j-1， 如果不选，状态转移到dp[i][j-1]

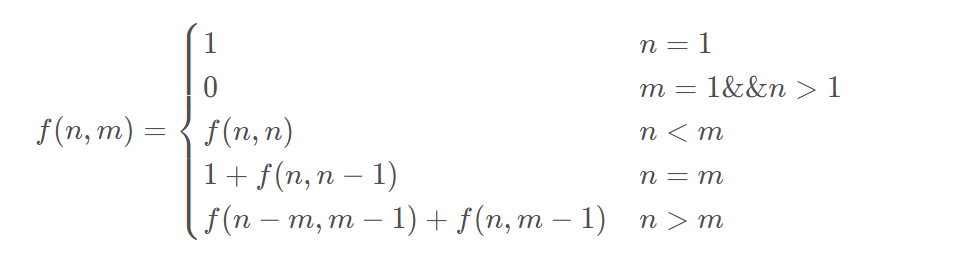
（5）分成恰好k个正整数

　　（a）设dp[i][j] 表示把数字 i 分成 j 个正整数之和所得的方法数

　　（b）递推公式核心：

• 这j个数里面含不含有1
  • 　　若不含1，则先为每份预分配一个1，再对i-j进行分割成j份；
  • 　　若含1，则先分出一个1， 然后再对剩下的的i-1分成 j-1份

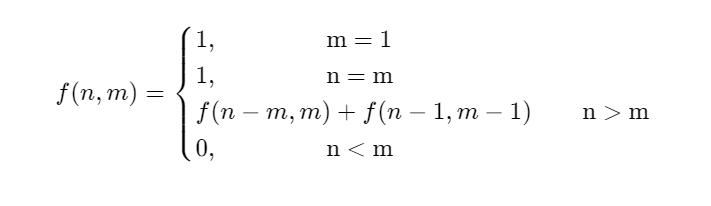
【记忆化搜索代码】

#include<iostream>
#include<queue>
#include<list>
#include<vector>
#include<cstring>
#include<set>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<cmath>
#include<algorithm>
#include<string>
#include<stdio.h>
using namespace std;
typedef long long ll;
const double eps=1e-;
const double PI = acos(-1.0);
const int inf = 0x3f3f3f3f;
const ll INF = 0x7fffffff;
#define MS(x,i) memset(x,i,sizeof(x))
#define rep(i,s,e) for(int i=s; i<=e; i++)
#define sc(a) scanf("%d",&a)
#define scl(a) scanf("%lld",&a)
#define sc2(a,b) scanf("%d %d", &a, &b)
#define dubug printf("debug......\n");
const int maxn = 1e2+;
int dx[] = {, , , -};
int dy[]  = {, -,  , };

/*
1. 把n划分成若干正整数之和 最大数不超过m 方法数
2. 把n划分成不超过m个正整数之和 方法数
1.2 等价
*/
ll dp1[maxn][maxn];
ll dp2[maxn][maxn];
ll dp3[maxn][maxn];
ll dp4[maxn][maxn];

//把n划分成不超过m的若干正整数之和     把n划分成不超过m个正整数之和 方法数
ll DP1(int n, int m){
    if(dp1[n][m] != -){
        return dp1[n][m];
    }
    ll ans = ;
    if(m ==  || n == ){
        return dp1[n][m] = ;
    }
    if(m == n){
        return dp1[n][m] = DP1(n , m - ) + ;
    }
    if(m > n){
        return dp1[n][m] = DP1(n,n);
    }
    if(m < n){
        return dp1[n][m] = DP1(n-m, m) + DP1(n , m-);
    }
    return dp1[n][m] = ;
}

//把N分成不超过m的，若干个正奇数的和 的方法数
ll DP2(int n , int m){
    if(dp2[n][m] != -) return dp2[n][m];

    if(n ==  || m == ){
        return dp2[n][m] = ;
    }
    if(n == m){
        return dp2[n][m] = DP2(n , m-) + m%;
    }
    if(n < m){
        return dp2[n][m] = DP2(n , n);
    }
    if(n > m){
        if(m % ){
            return dp2[n][m] = DP2(n-m , m) + DP2(n , m-);
        }
        else{
            return dp2[n][m] = DP2(n , m - );
        }
    }
    return dp2[n][m] = ;
}

//把N划分成不超过m的 不同正整数之和 的方法数
ll DP3(int n, int m){
    if(dp3[n][m] != -){
        return dp3[n][m];
    }
    if(n == ) return dp3[n][m] = ;
    if(m ==  && n > ){
        return dp3[n][m] = ;
    }

    if(m == n){
        return dp3[n][m] = DP3(n , m - ) + ;
    }
    if(m > n){
        return dp3[n][m] = DP3(n,n);
    }
    if(m < n){
        return dp3[n][m] = DP3(n-m, m-) + DP3(n , m-);
    }
    return dp3[n][m] = ;
}

//把n换分成恰好k个正整数之和
ll DP4(int n, int k){
    if(dp4[n][k] != -) return dp4[n][k];
    if(n ==  && k > ) return dp4[n][k] = ;
    if(k == ) return dp4[n][k] = ;
    if(n == k) return dp4[n][k] = ;
    if(n < k) return dp4[n][k] = ;
    if(n > k) return dp4[n][k] = DP4(n-k , k) + DP4(n-, k-);
    return ;
}

int n,m;
int k;
int main(){
    while(sc(n) != EOF){
        MS(dp1, -);
        MS(dp2 , -);
        MS(dp3 , -);
        MS(dp4 , -);
        sc(k);
        //printf("%lld\n", DP1(n,n));
        printf("%lld\n", DP4(n,k));
       // printf("%lld\n", DP1(n,k));
        printf("%lld\n", DP3(n,n));
         printf("%lld\n", DP2(n,n));

    }

    return ;
}

【DP代码】

#include<iostream>
#include<queue>
#include<list>
#include<vector>
#include<cstring>
#include<set>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<cmath>
#include<algorithm>
#include<string>
#include<stdio.h>
using namespace std;
typedef long long ll;
const double eps=1e-;
const double PI = acos(-1.0);
const int inf = 0x3f3f3f3f;
const ll INF = 0x7fffffff;
#define MS(x,i) memset(x,i,sizeof(x))
#define rep(i,s,e) for(int i=s; i<=e; i++)
#define sc(a) scanf("%d",&a)
#define scl(a) scanf("%lld",&a)
#define sc2(a,b) scanf("%d %d", &a, &b)
#define dubug printf("debug......\n");
const int maxn = 1e2+;
int dx[] = {, , , -};
int dy[]  = {, -,  , };

int n;
int k;
ll dp1[maxn][maxn];//把n划分成若干正整数之和且最大数不超过m    方法数   或者   把n划分成不超过m个正整数之和 方法数
ll dp2[maxn][maxn];//把N分成不超过m的，若干个【正奇数】的和 的方法数
ll dp3[maxn][maxn];//把N划分成不超过m的 【不同】正整数之和的方法数
ll dp4[maxn][maxn];//把n换分成【恰好k个】正整数之和

//把n划分成若干正整数之和且最大数【不超过m】    方法数   或者   把n划分成不超过【m个】正整数之和 方法数
void DP1(){
    MS(dp1, );
    rep(i,,n){
        rep(j,,n){
            if(i ==  || j ==  ){
                dp1[i][j] = ;
                continue;
            }
            if(j < i)
                dp1[i][j] = dp1[i-j][j] + dp1[i][j-];
            else if(j > i)
                dp1[i][j] = dp1[i][i];
            else
                dp1[i][j] = dp1[i][j-] + ;
        }
    }
}

//把N分成不超过m的，若干个【正奇数】的和 的方法数
void DP2(){
    MS(dp2, );
    rep(i,,n){
        rep(j,,n){
            if(i ==  || j == ){
                dp2[i][j] = ;
                continue;
            }
            if(j < i){
                if(j % )
                    dp2[i][j] = dp2[i-j][j] + dp2[i][j-];
                else{
                    dp2[i][j] = dp2[i][j-];
                }
            }
            else if(j == i){
                dp2[i][j] = j% + dp2[i][j-];
            }
            else
                dp2[i][j] = dp2[i][i];
        }
    }
}

//把N划分成不超过m的 【不同】正整数之和的方法数
void DP3(){
    MS(dp3, );
    rep(i,,n){
        rep(j,,n){
            if(i ==  ){
                dp3[i][j] = ;
                continue;
            }
            if(j ==  && i > ){
                dp3[i][j] = ;
                continue;
            }
            if(i < j) dp3[i][j] = dp3[i][i];
            if(i == j ){
                dp3[i][j] =  + dp3[i][j-];
            }
            if(i > j){
                dp3[i][j] = dp3[i-j][j-] + dp3[i][j-];
            }
        }
    }
   // cout<<dp3[5][5]<<endl;
}

//把n换分成【恰好k个】正整数之和
void DP4(){
    MS(dp4 , );
    rep(i, , n) {
        rep(j , , n){
            // if(i == 1 && j > 1) {
            //     dp4[i][j] = 0;
            //     continue;
            // }
            if(j == ) {
                dp4[i][j] = ;
                continue;
            }
            if(i == j) dp4[i][j] = ;
            if(i > j)
                dp4[i][j] = dp4[i-j][j] + dp4[i-][j-];
            if(i < j)
                dp4[i][j] = ;
        }
    }
}

int main(){
    while(sc(n) != EOF){
        sc(k);
        DP1();
        DP2();
        DP3();
        DP4();
        cout<<dp4[n][k]<<endl;
        cout<<dp3[n][n]<<endl;
        cout<<dp2[n][n]<<endl;
    }

    return ;
}

• （1）（2）等价旋转图来自博客：https://blog.csdn.net/starter_____/article/details/83003200