bzoj 4407 于神之怒加强版 （反演+线性筛）

于神之怒加强版

Time Limit: 80 Sec  Memory Limit: 512 MB
Submit: 1184  Solved: 535
[Submit][Status][Discuss]

Description

给下N,M,K.求

 

 

Input

输入有多组数据，输入数据的第一行两个正整数T,K，代表有T组数据，K的意义如上所示，下面第二行到第T+1行，每行为两个正整数N,M，其意义如上式所示。

Output

如题

Sample Input

1 2
3 3

Sample Output

20

HINT

1<=N,M,K<=5000000,1<=T<=2000

题解：JudgeOnline/upload/201603/4407.rar

Source

命题人：成都七中张耀楠，鸣谢excited上传。

 

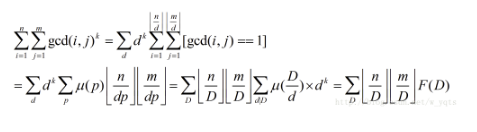
 #include<bits/stdc++.h>
 #pragma GCC optimize(2)
 #pragma G++ optimize(2)
 #include<iostream>
 #include<algorithm>
 #include<cmath>
 #include<cstdio>
 #include<cstring>

 #define ll long long
 #define inf 1000000000
 #define mod 1000000007
 #define N 5000007
 using namespace std;
 inline int read()
 {
     int x=,f=;char ch=getchar();
     while(!isdigit(ch)){if(ch=='-')f=-;ch=getchar();}
     while(isdigit(ch)){x=(x<<)+(x<<)+ch-'';ch=getchar();}
     return x*f;
 }

 int F[N],f[N],flag[N],k,tot,p[N],ans;
 inline int gpow(int x,int y)
 {
     int ans=;
     while (y)
     {
         if (y&) ans=(ll)ans*x%mod;
         y>>=;x=(ll)x*x%mod;
     }
     return ans;
 }
 void preparation()
 {
     F[]=;
     for (int i=;i<N;i++)
     {
         if (!flag[i]){f[i]=gpow(i,k);F[i]=f[i]-;p[++tot]=i;}
         for (int j=;j<=tot&&i*p[j]<N;j++)
         {
             flag[i*p[j]]=;
             if (i%p[j])F[i*p[j]]=(ll)F[i]*F[p[j]]%mod;
             else{F[i*p[j]]=(ll)F[i]*f[p[j]]%mod;break;}
         }
     }
     for (int i=;i<N;i++) (F[i]+=F[i-])%=mod;
 }
 int main()
 {
     int Case=read();k=read();
     preparation();
     while (Case--)
     {
         int n=read(),m=read();if (n>m) swap(n,m);ans=;
         for (int i=,pos=;i<=n;i=pos+)
         {
             pos=min(n/(n/i),m/(m/i));
             (ans+=1LL*(n/i)*(m/i)%mod*(F[pos]-F[i-])%mod)%=mod;
         }
         printf("%d\n",(ans+mod)%mod);
     }
     return ;
 }