机器学习中正则化项L1和L2的直观理解

正则化（Regularization）

概念

L0正则化的值是模型参数中非零参数的个数。

L1正则化表示各个参数绝对值之和。

L2正则化标识各个参数的平方的和的开方值。

L0正则化

稀疏的参数可以防止过拟合，因此用L0范数（非零参数的个数）来做正则化项是可以防止过拟合的。

从直观上看，利用非零参数的个数，可以很好的来选择特征，实现特征稀疏的效果，具体操作时选择参数非零的特征即可。但因为L0正则化很难求解，是个NP难问题，就是难以优化，因此一般采用L1正则化。L1正则化是L0正则化的最优凸近似，比L0容易求解，并且也可以实现稀疏的效果。

L1、L2正则化

机器学习中几乎都可以看到损失函数后面会添加一个额外项，常用的额外项一般有两种，一般英文称作ℓ₁-norm和ℓ₂-norm，中文称作L1正则化和L2正则化，或者L1范数和L2范数。

L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓『惩罚』是指对损失函数中的某些参数做一些限制。对于线性回归模型，使用L1正则化的模型建叫做Lasso回归，使用L2正则化的模型叫做Ridge回归（岭回归）。下图是Python中Lasso回归的损失函数，式中加号后面一项α||w||₁即为L1正则化项。

下图是Python中Ridge回归的损失函数，式中加号后面一项即为L2正则化项。

一般回归分析中回归w表示特征的系数，从上式可以看到正则化项是对系数做了处理（限制）。L1正则化和L2正则化的说明如下：

• L1正则化是指权值向量w中各个元素的绝对值之和，通常表示为||w||₁
• L2正则化是指权值向量w中各个元素的平方和然后再求平方根（可以看到Ridge回归的L2正则化项有平方符号），通常表示为||w||₂

一般都会在正则化项之前添加一个系数，Python中用α表示，一些文章也用λ表示。这个系数需要用户指定。

那添加L1和L2正则化有什么用？下面是L1正则化和L2正则化的作用，这些表述可以在很多文章中找到。

• L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择
• L2正则化可以防止模型过拟合（overfitting）；一定程度上，L1也可以防止过拟合

稀疏模型与特征选择

上面提到L1正则化有助于生成一个稀疏权值矩阵，进而可以用于特征选择。

1. 为什么要生成一个稀疏矩阵？（实现参数的稀疏有什么好处吗？）

一个好处是可以简化模型，避免过拟合。因为一个模型中真正重要的参数可能并不多，如果考虑所有的参数起作用，那么可以对训练数据可以预测的很好，但是对测试数据就只能呵呵了。另一个好处是参数变少可以使整个模型获得更好的可解释性。这就是稀疏模型与特征选择的关系。

2.参数值越小代表模型越简单吗？

是的。为什么参数越小，说明模型越简单呢，这是因为越复杂的模型，越是会尝试对所有的样本进行拟合，甚至包括一些异常样本点，这就容易造成在较小的区间里预测值产生较大的波动，这种较大的波动也反映了在这个区间里的导数很大，而只有较大的参数值才能产生较大的导数。因此复杂的模型，其参数值会比较大。

L1和L2正则化的直观理解

这部分内容将解释为什么L1正则化可以产生稀疏模型（L1是怎么让系数等于零的），以及为什么L2正则化可以防止过拟合。

L1正则化和特征选择

假设有如下带L1正则化的损失函数：

其中J₀是原始的损失函数，加号后面的一项是L1正则化项，α是正则化系数。注意到L1正则化是权值的绝对值之和，J是带有绝对值符号的函数，因此J是不完全可微的。机器学习的任务就是要通过一些方法（比如梯度下降）求出损失函数的最小值。当我们在原始损失函数J₀后添加L1正则化项时，相当于对J₀做了一个约束。令L=α∑_w|w|，则J=J₀+L，此时我们的任务变成在L约束下求出J₀取最小值的解。考虑二维的情况，即只有两个权值w1和w2，此时L=|w1|+|w2|对于梯度下降法，求解J₀的过程可以画出等值线，同时L1正则化的函数L也可以在w¹w²的二维平面上画出来。如下图：

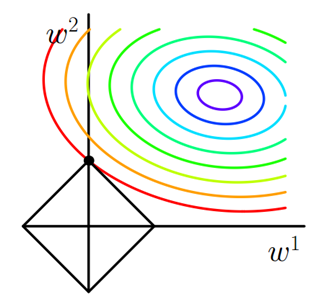
图1 L1正则化

图中等值线是J₀的等值线，黑色方形是L函数的图形。在图中，当J₀等值线与L图形首次相交的地方就是最优解。上图中J₀与L在L的一个顶点处相交，这个顶点就是最优解。注意到这个顶点的值是(w1,w2)=(0,w)。可以直观想象，因为L函数有很多『突出的角』（二维情况下四个，多维情况下更多），J₀与这些角接触的机率会远大于与L其它部位接触的机率，而在这些角上，会有很多权值等于0，这就是为什么L1正则化可以产生稀疏模型，进而可以用于特征选择。

而正则化前面的系数α，可以控制L图形的大小。α越小，L的图形越大（上图中的黑色方框）；α越大，L的图形就越小，可以小到黑色方框只超出原点范围一点点，这是最优点的值(w1,w2)=(0,w)中的w可以取到很小的值。

类似，假设有如下带L2正则化的损失函数：

同样可以画出他们在二维平面上的图形，如下：

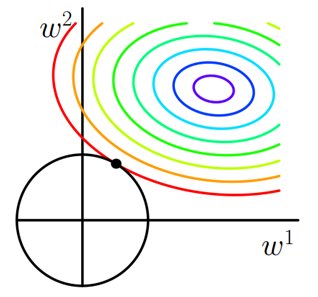
图2 L2正则化

二维平面下L2正则化的函数图形是个圆，与方形相比，被磨去了棱角。因此J₀与L相交时使得w₁或w₂等于零的机率小了许多，这就是为什么L2正则化不具有稀疏性的原因。

L2正则化和过拟合

避免过拟合的方式之一是使用交叉验证（cross validation），这有利于估计测试集中的错误，同时有利于确定对模型最有效的参数。本文将重点介绍一种方法，它有助于避免过拟合并提高模型的可解释性。

拟合过程中通常都倾向于让权值尽可能小，最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单，能适应不同的数据集，也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程，若参数很大，那么只要数据偏移一点点，就会对结果造成很大的影响；但如果参数足够小，数据偏移得多一点也不会对结果造成什么影响，专业一点的说法是『抗扰动能力强』。

正则化

正则化是一种回归的形式，它将系数估计（coefficient estimate）朝零的方向进行约束、调整或缩小。也就是说，正则化可以在学习过程中降低模型复杂度和不稳定程度，从而避免过拟合的危险。

那为什么L2正则化可以获得值很小的参数？

以线性回归中的梯度下降法为例。假设要求的参数为 是我们的假设函数，那么线性回归的代价函数如下：

那么在梯度下降法中，最终用于迭代计算参数θ的迭代式为：

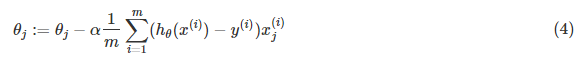
其中α是learning rate. 上式是没有添加L2正则化项的迭代公式，如果在原始代价函数之后添加L2正则化，则迭代公式会变成下面的样子：

 

其中λ就是正则化参数。从上式可以看到，与未添加L2正则化的迭代公式相比，每一次迭代，θ_j都要先乘以一个小于1的因子，从而使得θ_j不断减小，因此总得来看，θ是不断减小的。

最开始也提到L1正则化一定程度上也可以防止过拟合。之前做了解释，当L1的正则化系数很小时，得到的最优解会很小，可以达到和L2正则化类似的效果。

正则化参数的选择

L1正则化参数

通常越大的λ可以让代价函数在参数为0时取到最小值。下面是一个简单的例子，这个例子来自Quora上的问答。为了方便叙述，一些符号跟这篇帖子的符号保持一致。

假设有如下带L1正则化项的代价函数：

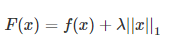
其中x是要估计的参数，相当于上文中提到的w以及θ. 注意到L1正则化在某些位置是不可导的，当λ足够大时可以使得F(x)在x=0时取到最小值。如下图：

图3 L1正则化参数的选择

分别取λ=0.5和λ=2，可以看到越大的λλ越容易使F(x)在x=0时取到最小值。

L2正则化参数

从公式5可以看到，λ越大，θ_j衰减得越快。另一个理解可以参考图2，λ越大，L2圆的半径越小，最后求得代价函数最值时各参数也会变得很小。

学习源于：https://blog.csdn.net/jinping_shi/article/details/52433975