洛谷P1962 斐波那契数列

传送门

不难得到状态转移矩阵

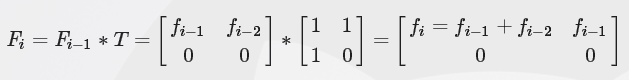
然后带进去乱搞

 //minamoto
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #define ll long long
 using namespace std;
 const int mod=1e9+;
 struct Matrix{
     ll g[][];
     Matrix(){memset(g,,sizeof(g));}
     Matrix(int Arr[][]){
         for(int i=;i<;++i) for(int j=;j<;++j)
         g[i][j]=Arr[i][j];
     }
     inline Matrix operator *(Matrix b){
         Matrix ans;
         for(int i=;i<;++i)
         for(int j=;j<;++j)
         for(int k=;k<;++k)
         (ans.g[i][j]+=g[i][k]*b.g[k][j])%=mod;
         return ans;
     }
 };
 ll n;
 int main(){
     scanf("%lld",&n);if(n<=) return puts(""),;
     n-=;
     int a[][]={{,},{,}};
     int b[][]={{,},{,}};
     Matrix A(a),B(b);
     while(n){
         if(n&) A=A*B;
         B=B*B,n>>=;
     }
     printf("%lld\n",A.g[][]);
     return ;
 }