洛谷P2826 LJJ的数学课

题目背景

题目描述（本题是提高组第二题难度＋）

题目描述

\(LJJ\)又要开始上数学课啦！（\(T1\)，永恒不变的数学）

\(LJJ\)的\(Teacher\)对上次的考试很不满意（其实是出题人对上次的分数那么高不满意啦），决定在出一道难（\(water\)）题。

---

\(LJJ\)的\(Teacher\)给了\(LJJ\)一个数列，但这由于是\(LJJ\)的\(Teacher\)发明的，我们不称呼他为\(LJJ\)数列，而称他为\(Teacher\)数列。但是\(LJJ\)还停留在数数的阶段啊，所以不能太难。

---

于是\(LJJ\)的\(Teacher\)随便给出了一个\(Teacher\)数列。

Teacher会对这个数列进行两个操作：

1：将其中的一个数加上s（s为整数）

2：Teacher会给出left和right，让你求：

a[left](right-left+1) + a[left+1](right-left)

• ...... + a[right-1]2 + a[right]1 的值。

即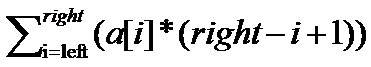

\(LJJ\)的指头掰不过来了呀，就请您来完成啦~

输入输出格式

输入格式：

第一行有\(2\)个数\(n,q\)，分别表示\(Teacher\)数列中数的个数以及操作次数。

接下来的一行有\(n\)个数，第\(i\)个数表示\(a[i]\)。

再接下来\(q\)行，每行三个数；第一个数是\(order\)。如果\(order=1\)，那么接下来两个数：\(x, s\)，即把\(a[x]\)加上\(s\)；如果\(order=2\)，那么接下来两个数：\(left, right\)，即求这一段区间\(LJJ\)要求的答案。

注意：\(Teacher\)数列中的数并不一定都是正数，但一定都是整数。

输出格式：

对于每一个询问\((order=2)\)输出所求答案

输入输出样例

输入样例#1：

5 3
2 4 1 3 5
2 2 4
1 2 3
2 2 4

输出样例#1：

17
26

说明

数据范围

\(n \leq 100000, q \leq 100000\)，保证答案不超过\(long\) \(long\) (\(int64\)) 范围，保证数据有梯度

样例解释

\(4*3+1*2+3*1=17\)

\(7*3+1*2+3*1=26\)

提示 \(1\).如果看不懂题目，那么看这里：给你一段数列，有两种操作，单点修改和区间查询。查询\(left\)到\(right\)，返回的值是

\(a[left]*(right-left+1)+a[left+1]*(right-left)+...+a[right]*1\)。

2.从另一个角度去想问题，把区间答案划分开来，否则你会打得很累。

3.题目中说是单点修改，而不是区间修改，有没有觉得简单得不可思议呢？

思路：把题目给的式子化一化，提出后面的\(right-1\)，变成\(a_{i}*(right+1)-a_{i}*i\)，整个式子变成\(\sum_{}(a_{i}*(right+1)-a_{i}*i)\)，用树状数组所以维护\(a_{i}*i\)和普通的加法和就好了。

代码：

#include<cstdio>
#include<cctype>
#define maxn 100007
#define lb(x) x&(-x)
#define ll long long
using namespace std;
ll n,m,a[maxn],b[maxn];
inline ll qread() {
  char c=getchar();ll num=0,f=1;
  for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
  for(;isdigit(c);c=getchar()) num=num*10+c-'0';
  return num*f;
}
inline void add(ll x, ll w) {
  ll p=x*w;
  while(x<=n) {
    a[x]+=w;
    b[x]+=p;
    x+=lb(x);
  }
}
inline ll csum1(ll x) {
  ll ans=0;
  while(x) {
    ans+=a[x];
    x-=lb(x);
  }
  return ans;
}
inline ll csum2(ll x) {
  ll ans=0;
  while(x) {
    ans+=b[x];
    x-=lb(x);
  }
  return ans;
}
int main() {
  n=qread(),m=qread();
  for(ll i=1,x;i<=n;++i) {
    x=qread();
    add(i,x);
  }
  for(ll i=1,k,l,r;i<=m;++i) {
    k=qread(),l=qread(),r=qread();
    if(k==1) add(l,r);
    else printf("%lld\n",(r+1)*(csum1(r)-csum1(l-1))-csum2(r)+csum2(l-1));
  }
  return 0;
}