[bzoj3071]N皇后

哈哈哈水题~

但是不能一眼看出来的。。我想了一个小时？！

---

题面

Description

“国际象棋中，一方的皇后数不能超过5个”

一个N*N的棋盘，任意摆放皇后，最坏情况下最少需要多少个皇后才能保证所有的格子都被攻击到。

Input

多组数据

第一行一个整数，数据组数T

接下来T行，每行一个正整数N

Output

每组数据输出一行一个整数表示答案。

Sample Input

1
3

Sample Output

3

HINT

100%的数据，N<=50，T<=25

---

真坑啊。。被数据范围骗了。。差点写了深搜。

然而事实是：

对于任意一个点A，这个地方放上皇后，A所能覆盖的点放上皇后也能覆盖A。

而A覆盖不了的点放上皇后怎么也覆盖不了A。

所以最优的方案就是，先在这些覆盖不了的点上全都放上皇后，最后就会只剩一个A没有覆盖，再怎么放A都要被覆盖了。

如下图

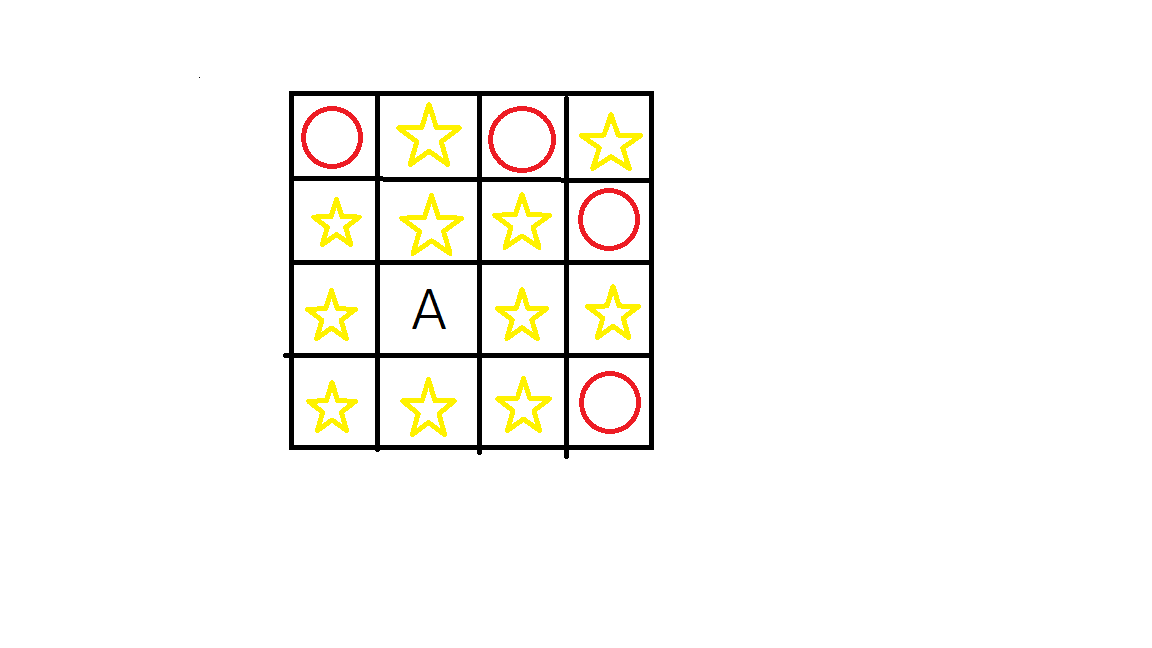
对于任意的A，红圈再加上随便一个位置就是要放的地方。

可以证明这个A取四个角的时候不能覆盖点最多。即答案最大。

所以答案就是n*n-n*3+3了。

代码简直智障。

 #include<cstdio>
 int main(){
     int t;scanf("%d",&t);
     while(t--){
         int n;scanf("%d",&n);
         printf("%d\n",n*(n-)+);
     }
 }