普林斯顿算法(1.3)并查集(union-find算法)——本质就是一个数 下面的子树代表了连在一起的点
转自:https://libhappy.com/2016/03/algs-1.3/
假设在互联网中有两台计算机需要互相通信,那么该怎么确定它们之间是否已经连接起来还是需要架设新的线路连接这两台计算机。这就是动态连通性问题。 动态连通性问题在日常生活中十分常见,比如上文所说的通信网络中的连通性问题,比如物理化学中的渗流问题。通过并查集这种数据结构及union-find 算法可以解决动态连通性问题。
动态连通性问题
概念
给出一系列的对象时,让其支持以下的两个操作:
- 判断两个对象是否相连
- 使两个对象相连
这里以整数代表对象,有0-9共十个整数,当给出一个整数对(a, b)时表示将整数a和b相连(如果a、b不相连)。如下图所示:
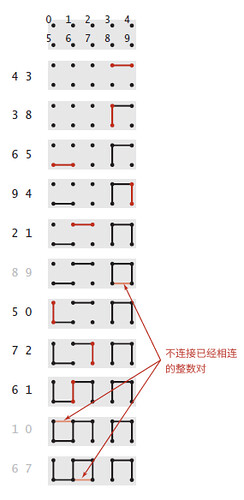
随着整数对的输入,十个整数的连通性会发生变化,这就是动态连通性问题。
在动态连通性问题中,我们假设“相连”是一种等价关系,也就意味着它具有:
- 自反性:p和p是相连的
- 对称性:如果p和q是相连的,那么q和p也是相连的
- 传递性:如果p和q是相连的且q和r是相连的,那么p和r是相连的。
在所有给出的对象中,所有相连的一组对象称为连通分量(Connected component)。如上图中最后一行的(0, 1, 2, 5, 6, 7)和(3, 4, 8, 9)分别为两个连通分量。
应用
- 计算机网络:判断网络中的计算机是否可以通过已存在的连接直接通信;
- 社交网络中的朋友关系:将朋友关系当作相连,判断两个人之间的朋友关系;
- 计算机芯片中晶体管的连接问题:判断芯片中晶体管是否相连;
- 变量名的等价性:某些编程语言(如FORTRAN)中允许声明两个等价的变量名,判断两个给定的变量名是否等价;
- 数学集合中的元素:元素可能属于不同的集合,将元素“相连”表示将两个元素所属的集合合并成一个集合。
如在下图所示的所有连接中判断p和q点之间是否相连。
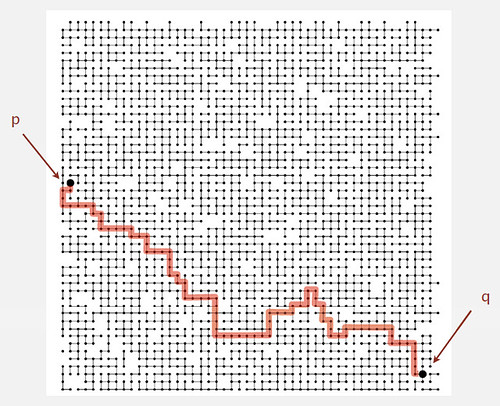
设计算法
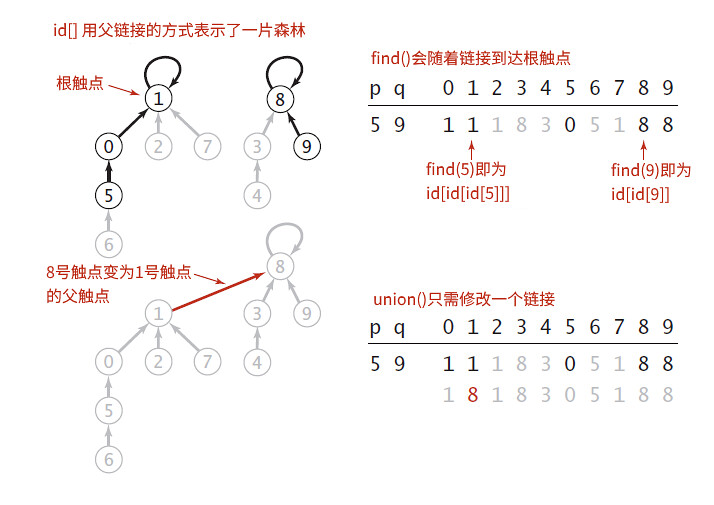
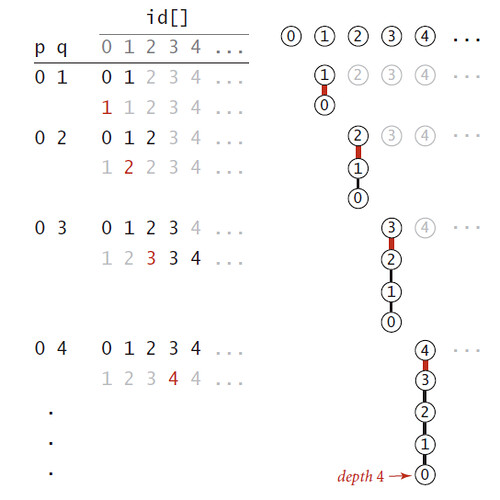
普林斯顿算法(1.3)并查集(union-find算法)——本质就是一个数 下面的子树代表了连在一起的点的更多相关文章
- 并查集(Union/Find)模板及详解
概念: 并查集是一种非常精巧而实用的数据结构,它主要用于处理一些不相交集合的合并问题.一些常见的用途有求连通子图.求最小生成树的Kruskal 算法和求最近公共祖先等. 操作: 并查集的基本操作有两个 ...
- hdu 4641 K-string SAM的O(n^2)算法 以及 SAM+并查集优化
链接:http://acm.hdu.edu.cn/showproblem.php?pid=4641 题意:有一个长度为n(n < 5e4)的字符串,Q(Q<=2e5)次操作:操作分为:在末 ...
- hdu 1233(还是畅通project)(prime算法,克鲁斯卡尔算法)(并查集,最小生成树)
还是畅通project Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Tota ...
- 最小生成数(并查集)Kruskal算法
并查集:使用并查集可以把每个连通分量看作一个集合,该集合包含连通分量的所有点.这两两连通而具体的连通方式无关紧要,就好比集合中的元素没有先后顺序之分,只有属于和不属于的区别.#define N 100 ...
- 并查集实现Tarjan算法
本文是对http://noalgo.info/476.html的一点理解,特别是对其中 int father[mx]: //节点的父亲 int ancestor[mx]; //已访问节点集合的祖先 这 ...
- POJ 2421 Constructing Roads (Kruskal算法+压缩路径并查集 )
Constructing Roads Time Limit: 2000MS Memory Limit: 65536K Total Submissions: 19884 Accepted: 83 ...
- hdu 4641K-string SAM的O(n^2)算法 以及 SAM+并查集优化
转载:http://www.cnblogs.com/hxer/p/5675149.html 题意:有一个长度为n(n < 5e4)的字符串,Q(Q<=2e5)次操作:操作分为:在末尾插入一 ...
- 距离LCA离线算法Tarjan + dfs + 并查集
距离B - Distance in the Tree 还是普通的LCA但是要求的是两个节点之间的距离,学到了一些 一开始我想用带权并查集进行优化,但是LCA合并的过程晚于离线计算的过程,所以路径长度会 ...
- POJ 1611 The Suspects 并查集 Union Find
本题也是个标准的并查集题解. 操作完并查集之后,就是要找和0节点在同一个集合的元素有多少. 注意这个操作,须要先找到0的父母节点.然后查找有多少个节点的额父母节点和0的父母节点同样. 这个时候须要对每 ...
随机推荐
- LeetCode78:Subsets
Given a set of distinct integers, nums, return all possible subsets. Note: Elements in a subset must ...
- Project Euler:Problem 87 Prime power triples
The smallest number expressible as the sum of a prime square, prime cube, and prime fourth power is ...
- 详细的linux目录结构详细介绍
详细的linux目录结构详细介绍 --树状目录结构图 下面红色字体为比较重要的目录 1./目录 目录 描述 / 第一层次结构的根,整个文件系统层次结构的根目录 /bin/ 需要在单用户模式可用的必要命 ...
- unity一些知识
有一个问题就是在Inspector面板修改 WheelNumber的数值后,运行项目,当项目停止的时候,WheelNumber 的数据又回到以前的数据,(数据未保存成功,数据丢失) 解决办法需要在 修 ...
- 使用CSDN CODE来存放OPENSTACK位于GITHUB上的源代码
use CSDN CODE to pull openstack codes 2014-11-20 Author:Hyphen 问题 直接从GITHUB上获代替码,常常是没保障,特别是用DEVSTACK ...
- SQLServer2008 统计表占用空间
1.查看一张表占用的空间大小 EXEC sp_spaceused '表' 1.查看一个数据库中所有表占用空间大小 EXEC sp_MSforeachtable 'sp_spaceused " ...
- Q: Why can't I access the Site Settings of my SharePoint site? 'File Not Found'
Q: I am trying to access the Site Settings of my SharePoint site, but I get a File Not Found error, ...
- python 捕获异常详细信息
import os import sys import traceback BasePath = os.path.dirname(os.getcwd()) sys.path.append(BasePa ...
- require.js vs browserify
require.js vs browserify require.js是模块加载器:browserify是预编译工具 require.js遵循的是AMD规范:browserify遵循的是CommonJ ...
- php自定义的格式化时间示例代码
时间刚好是5分钟前,则对应的时间戳就会被格式化为5分钟前,自定义的格式化时间方法如下,感兴趣的朋友可以参考下 如:时间刚好是5分钟前,则对应的时间戳就会被格式化为5分钟前,不多说了,直接贴上代码: 复 ...
