The 2013 ACMICPC Asia Regional Chengdu
还有19天出发北京站，今年北京站的出题方是上交，去年他们出的成都现场的赛题，首先复盘一下。
去年的成都是我经历的第一次现场赛，也是近距离第一次见到了CLJ的真人，最后也是被虐惨了，那时候是声闻大神带着我们去的，也是在那次现场之后，深深地感受到了差距。现在我们进步了，只可惜选手都在发展，比赛也在发展，别人大概是进步得更多吧，上场西安赛站也只能遗憾。
没想到最后一场居然又能碰到开场第一次能够遇上的出题方，也是个奇妙的巧合吧。
【B】模拟
【C】-_-///
【E】计算几何
【G】在线AC自动机
【I】模拟（用STL中的set）
----------------------------------------------------
【A】 HDU 4781
Assignment For Princess
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Special Judge
【Problem Description】
Long long ago, in the Kingdom Far Far Away, there lived many little animals. And you are the beloved princess who is marrying the prince of a rich neighboring kingdom. The prince, who turns out to be a handsome guy, offered you a golden engagement ring that can run computer programs!
The wedding will be held next summer because your father, the king, wants you to finish your university first.
But you did’t even have a clue on your graduation project. Your terrible project was to construct a map for your kingdom. Your mother, the queen, wanted to make sure that you could graduate in time.
Or your wedding would have to be delayed to the next winter. So she told you how your ancestors built the kingdom which is called the Roads Principle:
1. Your kingdom consists of N castles and M directed roads.
2. There is at most one road between a pair of castles.
3. There won’t be any roads that start at one castle and lead to the same one.
She hoped those may be helpful to your project. Then you asked your cousin Coach Pang (Yes, he is your troubling cousin, he always asks you to solve all kinds of problems even you are a princess.), the Minister of Traffic, about the castles and roads. Your cousin, sadly, doesn’t have a map of the kingdom. Though he said the technology isn’t well developed and it depends on your generation to contribute to the map, he told you the Travelers Guide, the way travelers describe the amazing road system:
1. No matter which castle you start with, you can arrive at any other castles.
2. Traveling on theM roads will take 1, 2, 3, ... ,M days respectively, no two roads need the same number of days.
3. You can take a round trip starting at any castle, visiting a sequence of castles, perhaps visiting some castles or traveling on some roads more than once, and finish your journey where you started.
4. The total amount of days spent on any round trip will be a multiple of three.
But after a month, you still couldn’t make any progress. So your brother, the future king, asked your university to assign you a simpler project. And here comes the new requirements. Construct a map that satisfies both the Roads Principle and the Travelers Guide when N and M is given.
There would probably be several solutions, but your project would be accepted as long as it meets the two requirements. Now the task is much easier, furthermore your fiance sent two assistants to help you.
Perhaps they could finish it within 5 hours and you can think of your sweet wedding now.
【Input】
The first line contains only one integer T, which indicates the number of test cases. For each test case, there is one line containing two integers N, M described above.(10 <= N <= 80, N+3 <= M <= N2/7 )
【Output】
For each test case, first output a line “Case #x:”, where x is the case number (starting from 1).
Then output M lines for each test case. Each line contains three integers A, B, C separated by single space, which denotes a road from castle A to castle B and the road takes C days traveling.
Oh, one more thing about your project, remember to tell your mighty assistants that if they are certain that no map meets the requirements, print one line containing one integer -1 instead.
Note that you should not print any trailing spaces.
【Sample Input】
【Sample Output】
Case #:
【Hint】
The restrictions like N >= 10 will be too big for a sample. So the sample is just a simple case for the detailed formats of input and output,
and it may be helpful for a better understanding. Anyway it won’t appear in actual test cases.
【题意】
要求构造一张图，同时满足以下7个条件：
1.有n个点和m条有向边；
2.两点点之间无重边；
3.无自环；
4.整张图都是连通的；
5.m条边的长度分别为1、2、...、m；
6.从任意一点出发都能够回到出发点，点和边可多次经过。
7.每一次Travel走过的总长度都一定是3的倍数。
【分析】
前面几个条件都是对图的基本性质的保证。从一次Traval可重复经过点和边的性质+Travel总长度是3的倍数这两个条件入手，分析一下即所有有向环的总长都是3的倍数。
首先构造一个简单的回路，从1至n每两点依次连边，这样就用掉了1~n-1，第n条边放上n、n+1或者n+2使得第一个环总长为三的倍数。
接下来就是把剩下那些边放到图中去了，然后需要的是在放边的同时保持原有的图的性质不变。设下一条要放上去的边长为x，dist[i][j]表示点i与点j之间的路径长度，则(dist[i][j]+dist[j][i])%3==0，也即dist[i][j]%3+dist[j][i]%3==3。则对于x，找到两个点i、j使得dist[i][j]%3==x%3，则在i、j之间加上边x之后x就能够替代原来的长边，构成一个新的总长为3的倍数的有向环。依次解决完所有的剩余边即可。
/* ***********************************************
MYID : Chen Fan
LANG : G++
PROG : HDU 4781
************************************************ */ #include <iostream>
#include <cstdio>
#include <cstring> using namespace std; int mapl[][],dist[][];
bool use[]; int main()
{
int t,n,m;
scanf("%d",&t);
for (int tt=;tt<=t;tt++)
{
printf("Case #%d:\n",tt);
scanf("%d%d",&n,&m);
int tot=;
bool bq=false;
memset(mapl,,sizeof(mapl));
memset(dist,-,sizeof(dist)); for (int i=;i<n;i++)
{
tot+=i;
mapl[i][i+]=i;
dist[i][i+]=i;
} for (int i=n;i<n+;i++)
if ((tot+i)%==)
{
mapl[n][]=i;
dist[n][]=i;
break;
} memset(use,,sizeof(use));
use[mapl[n][]]=true; for (int i=;i<=n;i++)
for (int j=;j<=n;j++)
if (i!=j)
for (int k=;k<=n;k++)
if (i!=k&&j!=k)
if (dist[j][i]>&&dist[i][k]>)
if (dist[j][k]==-) dist[j][k]=dist[j][i]+dist[i][k]; for (int i=;i<=n;i++)
for (int j=;j<=n;j++)
if (dist[i][j]>-) dist[i][j]%=; //for (int i=1;i<=n;i++)
//for (int j=1;j<=n;j++) printf("%d %d %d\n",i,j,dist[i][j]); for (int i=n;i<=m;i++)
{
if (!use[i])
{
for (int j=;j<=n;j++)
for (int k=;k<=n;k++)
if (!use[i])
if (mapl[j][k]==&&mapl[k][j]==&&dist[j][k]>-&&dist[j][k]%==i%)
{
mapl[j][k]=i;
use[i]=true;
}
}
if (!use[i])
{
printf("-1\n");
bq=true;
break;
}
} if (!bq)
for (int i=;i<=n;i++)
for (int j=;j<=n;j++)
if (mapl[i][j]>) printf("%d %d %d\n",i,j,mapl[i][j]);
} return ;
}
【D】 HDU 4784
Dinner Coming Soon
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 102400/102400 K (Java/Others)
【Problem Description】
Coach Pang loves his boyfriend Uncle Yang very much. Today is Uncle Yang’s birthday, Coach Pang wants to have a romantic candlelit dinner at Uncle Yang’s house and he has to arrive there in T minutes.
There are N houses in their city numbered from 1 to N. Coach Pang lives in house 1 while Uncle Yang lives in house N. The houses are connected byM directed roads. It takes some time and usually a fee to pass one road. Coach Pang wants to reach Uncle Yang’s house before the dinner starts with as much money as possible.
But the matter is not so simple. Coach Pang decides to do some salt trade on the way to Uncle Yang’s house. The host of each house offers a price of a bag of salt, so Coach Pang can make a profit from the price differences. Each time when Coach Pang arrives at a house (except the house 1 and the house N). He can buy one bag of salt, sell one bag of salt or do nothing. Coach Pang can carry at most B bags of salt with him, and he carries no salt when he leaves his house. The trading is so efficient that the time cost of trading can be ignored.
However, the problem is more complicated than imagine. Coach Pang has a handheld device that can perform a journey around K parallel universes numbered from 0 to K-1. Coach Pang lives in the universe 0. When Coach Pang uses the device in universe i, he will be transported to the same place and the same time of universe (i+1) modK. The host of the house at the same place in different universe may offer a different price of salt. Luckily, the time cost and fee of the city roads are uniform among the K universes. The journey between universes costs no time but Coach Pang has to stand still watching the ads on the device for one minute every time before the device works. Remember, Coach Pang should never visit house 1 or house N in a universe other than universe 0, because the situation might become uncontrollable if he bumps into himself or his boyfriend in another universe.
The time is running out. Coach Pang asks you to tell him whether he can arrive at Uncle Yang’s house in time, and how much money Coach Pang can have at most when the dinner starts. Coach Pang has R yuan at the start, and will end his journey immediately once he arrives at Uncle Yang’s house. He must arrive at Uncle Yang’s house in T minutes, and he can’t have negative amount of money anywhere anytime. Please help him!
【Input】
The first line of the input is an integer C representing the number of test cases.
For each test case, the first line will contain 6 integers N, M, B, K, R, T, as described above.
(2 <= N <= 100, 0 <= M <= 200, 1 <= B <= 4, 2 <= K <= 5, 0 <= R <= 105, 0 <= T <= 200)
The following K lines contain N integers each, indicating the price pij (0 <= i < K, 1 <= j <= N) for a bag of salt offered by the host of house j in the universe i. The price of house 1 and house N will be marked as -1.(1 <= pij <= 100)
Then M lines follow, each contains 4 integers a, b, t and m, indicating that there is a road from house a to house b that costs t minutes of time and m yuan of money. (1 <= a,b <= N, a<> b, 1 <= t <=15, 0 <= m <= 100)
【Output】
For each test case, output one line containing “Case #x: y”, where x is the case number (starting from 1) and y is the most money Coach Pang can have if he can have dinner with Uncle Yang on time.
Print "Forever Alone" otherwise.
【Sample Input】
- -
- - - -
- -
【Sample Output】
Case #:
Case #: Forever Alone
【题意】
给出一张有向图，主人公需要在时间T之内从编号为1的点走到编号为n的点。图中存在一个货币系统，主人公在初始状态的时候身上有R单位的货币，在图中除了1和n之外的所有点都可以买进或者卖出一包盐，每一个点的盐价不同，因此主人公可以通过这种方式在不同的位置进行盐的买卖赚取收益。图中的每一条有向边都有两个代价，时间花费和货币花费，而且除此之外这张图中还有K个“平行世界”，分别标记为0~K-1，在每个不同的平行世界中每个点的盐价也不同，主人公可以花费1单位时间从第i个平行世界的某个点中跳跃到第(i+1)%K个平行世界的同一个点上，唯一的限制是1点和n点只能从第0个平行世界中进入，且一旦到达第n点，这次遍历就结束了。
现在，最终的问题就是主人公从1点出发走到n点，身上最多可能持有多少单位的货币。
【分析】
写这道题的时候代码遭遇神坑啊！！！！
首先构图非常简单，相对于一般的图，本题只是把普通的单一代价有向边再加上一个代价，平行世界的跳转只是从i跳到(i+1)%k，且花费只有1单位时间。对于图中每一个点的情况，很容易能够想到状态转移方程式，用f(i,j,k,l)表示当前在第i点，花费了j时间，手上持有k包盐，目前在平行世界k的最大持有货币数。出现的位置状态转移只有两种：沿着有向边走向下一个点或者进行平行世界跳转。位置转移完成之后，接下来发生的价值转移有三种，不作任何操作、买入一包盐或者卖出一包盐。大致的方程是这样的，这里省略了一些转移条件：
f(i,j,k,l)=max{ f(p,j+edge[i,p].time,k,l),
f(p,j+edge[i,p].time,k+1,l)-price[l][p],
f(p,j+edge[i,p].time,k-1,l)+price[l][p],
f(i,j+1,k,(l+1)%K),
f(i,j+1,k+1,(l+1)%K)-price[(l+1)%K][i],
f(i,j+1,k-1,(l+1)%K)+price[(l+1)%K][i] }
最直接的想法是使用SPFA作为整体的DP框架，虽然整体数据范围不太大，但是这里反复进出队列的话，超时的可能性非常大。这里DP遇到的最大问题是后效性，关于这一点，我们可以看到状态递推的方向是花费时间增加的方向。普通的SPFA不能保证后面加入队列的状态时间一定是递增的，因此需要反复多次进出队列，所以在这里使用一个花费时间递增的优先队列来替换掉SPFA中的普通队列，保证状态按照花费时间递增的顺序来扩展，就能解决DP的后效性问题，记录一下加入过队列的点不用再次加入即可节省下来大量的时间。
写代码的时候因为一点失误被坑了好久......吸取的教训是：DP中后续的六种状态的值必须从原始状态出发！其实这个原本是非常直观的，写到图论的结构里面之后因为代码太多了，居然简单地就直接从1往2、3写，从4往5、6写了。
/* ***********************************************
MYID : Chen Fan
LANG : G++
PROG : HDU4784
************************************************ */ #include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue> using namespace std; typedef struct nod{
int a,b,c,d;
} node; int start[],num[];
int p[][];
int n,m,b,k,r,tim;
node edge[]; typedef struct qnod
{
int s,t,b,k;
friend bool operator < (qnod a,qnod b)
{
return a.t>b.t;
}
} qnode; int f[][][][]; bool op(node a,node b)
{
return a.a<b.a;
} int main()
{
freopen("test.txt","r",stdin); int t;
scanf("%d",&t);
for (int tt=;tt<=t;tt++)
{
scanf("%d%d%d%d%d%d",&n,&m,&b,&k,&r,&tim);
for (int i=;i<k;i++)
for (int j=;j<=n;j++) scanf("%d",&p[i][j]);
for (int i=;i<=m;i++) scanf("%d%d%d%d",&edge[i].a,&edge[i].b,&edge[i].c,&edge[i].d);
sort(&edge[],&edge[m+],op); int o=;
memset(num,,sizeof(num));
for (int i=;i<=m;i++)
{
if (o!=edge[i].a)
{
o=edge[i].a;
start[o]=i;
}
num[o]++;
} printf("Case #%d: ",tt); priority_queue<qnode> q;
while (!q.empty()) q.pop();
memset(f,-,sizeof(f)); qnode st;
st.s=;st.t=;st.b=;st.k=;
f[][][][]=r;
q.push(st); int ans=-;
while (!q.empty())
{
qnode now=q.top();
q.pop(); for (int i=;i<num[now.s];i++)
{
qnode next;
int mm=f[now.s][now.t][now.b][now.k]-edge[start[now.s]+i].d;
next.t=now.t+edge[start[now.s]+i].c;
if (mm<||next.t>tim) continue;
next.s=edge[start[now.s]+i].b;
next.b=now.b;
next.k=now.k; if (next.s==&&next.k!=) continue;
if (next.s==n)
{
if (next.k!=) continue;
if (ans<mm) ans=mm;
} else
{
if (f[next.s][next.t][next.b][next.k]<) q.push(next);
if (f[next.s][next.t][next.b][next.k]<mm) f[next.s][next.t][next.b][next.k]=mm; if (next.s==) continue;
if (next.b<b&&f[next.s][next.t][next.b][next.k]>=p[next.k][next.s])
{
qnode temp=next;
temp.b++;
mm=f[now.s][now.t][now.b][now.k]-edge[start[now.s]+i].d-p[next.k][next.s]; //!!!!!
if (f[temp.s][temp.t][temp.b][temp.k]<) q.push(temp);
if (f[temp.s][temp.t][temp.b][temp.k]<mm) f[temp.s][temp.t][temp.b][temp.k]=mm;
} if (next.b>)
{
qnode temp=next;
temp.b--;
mm=f[now.s][now.t][now.b][now.k]-edge[start[now.s]+i].d+p[next.k][next.s];
if (f[temp.s][temp.t][temp.b][temp.k]<) q.push(temp);
if (f[temp.s][temp.t][temp.b][temp.k]<mm) f[temp.s][temp.t][temp.b][temp.k]=mm;
}
}
}
if (now.s==) continue;
qnode next=now;
int mm=f[now.s][now.t][now.b][now.k];
next.k=(next.k+)%k;
next.t++;
if (next.t>tim) continue; if (f[next.s][next.t][next.b][next.k]<) q.push(next);
if (f[next.s][next.t][next.b][next.k]<mm) f[next.s][next.t][next.b][next.k]=mm; if (next.b<b&&f[next.s][next.t][next.b][next.k]>=p[next.k][next.s])
{
qnode temp=next;
temp.b++;
mm=f[now.s][now.t][now.b][now.k]-p[next.k][next.s];
if (f[temp.s][temp.t][temp.b][temp.k]<) q.push(temp);
if (f[temp.s][temp.t][temp.b][temp.k]<mm) f[temp.s][temp.t][temp.b][temp.k]=mm;
} if (next.b>)
{
qnode temp=next;
temp.b--;
mm=f[now.s][now.t][now.b][now.k]+p[next.k][next.s];
if (f[temp.s][temp.t][temp.b][temp.k]<) q.push(temp);
if (f[temp.s][temp.t][temp.b][temp.k]<mm) f[temp.s][temp.t][temp.b][temp.k]=mm;
}
} if (ans<) printf("Forever Alone\n");
else printf("%d\n",ans);
} return ;
}
【F】 HDU 4786
Fibonacci Tree
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
【Problem Description】
Coach Pang is interested in Fibonacci numbers while Uncle Yang wants him to do some research on Spanning Tree. So Coach Pang decides to solve the following problem: Consider a bidirectional graph G with N vertices and M edges. All edges are painted into either white or black. Can we find a Spanning Tree with some positive Fibonacci number of white edges? (Fibonacci number is defined as 1, 2, 3, 5, 8, ... )
【Input】
The first line of the input contains an integer T, the number of test cases. For each test case, the first line contains two integers N(1 <= N <= 105) and M(0 <= M <= 105). Then M lines follow, each contains three integers u, v (1 <= u,v <= N, u<> v) and c (0 <= c <= 1), indicating an edge between u and v with a color c (1 for white and 0 for black).
【Output】
For each test case, output a line “Case #x: s”. x is the case number and s is either “Yes” or “No” (without quotes) representing the answer to the problem.
【Sample Input】
【Sample Output】
Case #: Yes
Case #: No
【题意】
给出一张无向图，图中每一条边都有黑或者白两种颜色。询问是否可以从这张图中找到这样一个生成树，使得白边的条数为一个斐波那契数。
【分析】
考虑使用Kruskal构造最小生成树的方法，如果把颜色作为边权值，则可以构造出白边优先或者黑边优先的生成树。
白边优先树是尽可能多的取白边，能得到最多的使生成树成立的白边数，黑边优先树则是尽可能多的取黑边，得到最少的使生成树成立的白边数。从白边优先树出发的话，如果我们取掉一条白边，添加一条黑边，则构成的新图一定还是一棵树。即根据这个原理，可以构造出白边数介于最少白边数和最大白边数之间的所有生成树。接下来只要判断一下介于这两个数之间是不是存在斐波那契数即可。
/* ***********************************************
MYID : Chen Fan
LANG : G++
PROG : HDU4786
************************************************ */ #include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <bitset> typedef struct nod
{
int a,b,color;
} node; node edge[]; using namespace std; bool op(node a,node b)
{
return a.color<b.color;
} int n,m; int father[]; int getfather(int x)
{
if (father[x]!=x) father[x]=getfather(father[x]);
return father[x];
} void link(int x,int y)
{
father[getfather(x)]=getfather(y);
} int kruskal1()
{
for (int i=;i<=n;i++) father[i]=i;
int num=,tot=;
for (int i=;i<=m;i++)
if (getfather(edge[i].a)!=getfather(edge[i].b))
{
link(edge[i].a,edge[i].b);
if (edge[i].color) num++;
tot++;
}
if (tot!=n-) return -;
else return num;
} int kruskal2()
{
for (int i=;i<=n;i++) father[i]=i;
int num=,tot=;
for (int i=m;i>=;i--)
if (getfather(edge[i].a)!=getfather(edge[i].b))
{
link(edge[i].a,edge[i].b);
if (edge[i].color) num++;
tot++;
}
if (tot!=n-) return -;
else return num;
} int main()
{
int tot=;
bitset<>fbn;
fbn.reset();
int a=,b=,c;
fbn[]=;
while ()
{
c=a+b;
if (c>=) break;
fbn[c]=;
a=b;
b=c;
} int t;
scanf("%d",&t);
for (int tt=;tt<=t;tt++)
{
scanf("%d%d",&n,&m); for (int i=;i<=m;i++) scanf("%d%d%d",&edge[i].a,&edge[i].b,&edge[i].color); printf("Case #%d: ",tt); sort(&edge[],&edge[m+],op);
int b1=kruskal1(); if (b1<)
{
printf("No\n");
continue;
} int b2=kruskal2(); bool done=false;
for (int i=b1;i<=b2;i++)
if (fbn[i])
{
done=true;
break;
} if (done) printf("Yes\n");
else printf("No\n");
} return ;
}
【H】 HDU 4788
Hard Disk Drive
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
【Problem Description】
Yesterday your dear cousin Coach Pang gave you a new 100MB hard disk drive (HDD) as a gift because you will get married next year. But you turned on your computer and the operating system (OS) told you the HDD is about 95MB. The 5MB of space is missing. It is known that the HDD manufacturers have a different capacity measurement. The manufacturers think 1 “kilo” is 1000 but the OS thinks that is 1024. There are several descriptions of the size of an HDD. They are byte, kilobyte, megabyte, gigabyte, terabyte, petabyte, exabyte, zetabyte and yottabyte. Each one equals a “kilo” of the previous one. For example 1 gigabyte is 1 “kilo” megabytes. Now you know the size of a hard disk represented by manufacturers and you want to calculate the percentage of the “missing part”.
【Input】
The first line contains an integer T, which indicates the number of test cases. For each test case, there is one line contains a string in format “number[unit]” where number is a positive integer within [1, 1000] and unit is the description of size which could be “B”, “KB”, “MB”, “GB”, “TB”, “PB”, “EB”, “ZB”, “YB” in short respectively.
【Output】
For each test case, output one line “Case #x: y”, where x is the case number (starting from 1) and y is the percentage of the “missing part”. The answer should be rounded to two digits after the decimal point.
【Sample Input】
[MB]
[B]
【Sample Output】
Case #: 4.63%
Case #: 0.00%
【Hint】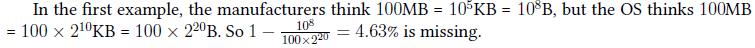
【分析】
签到题
【J】 HDU 4790
Just Random
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
【Problem Description】
Coach Pang and Uncle Yang both love numbers. Every morning they play a game with number together. In each game the following will be done:
1. Coach Pang randomly choose a integer x in [a, b] with equal probability.
2. Uncle Yang randomly choose a integer y in [c, d] with equal probability.
3. If (x + y) mod p = m, they will go out and have a nice day together.
4. Otherwise, they will do homework that day.
For given a, b, c, d, p and m, Coach Pang wants to know the probability that they will go out.
【Input】
The first line of the input contains an integer T denoting the number of test cases. For each test case, there is one line containing six integers a, b, c, d, p and m(0 <= a <= b <= 109, 0 <=c <= d <= 109, 0 <= m < p <= 109).
【Output】
For each test case output a single line "Case #x: y". x is the case number and y is a fraction with numerator and denominator separated by a slash ('/') as the probability that they will go out. The fraction should be presented in the simplest form (with the smallest denominator), but always with a denominator (even if it is the unit).
【Sample Input】
【Sample Output】
Case #: /
Case #: /
Case #: /
Case #: /
【题意】
给定两个区间，每次分别从这两个区间中取出一个数求和，问有多少种组合的和是能够对p取模之后等于m的概率。
【分析】
The 2013 ACMICPC Asia Regional Chengdu的更多相关文章
- HDU 4291 A Short problem(2012 ACM/ICPC Asia Regional Chengdu Online)
HDU 4291 A Short problem(2012 ACM/ICPC Asia Regional Chengdu Online) 题目链接http://acm.hdu.edu.cn/showp ...
- 2013 ACM/ICPC Asia Regional Chengdu Online 1004 Minimum palindrome
Minimum palindrome Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Other ...
- The 2013 ACM-ICPC Asia Changsha Regional Contest - K
Pocket Cube Time Limit: 2 Seconds Memory Limit: 65536 KB Pocket Cube is a 3-D combination puzzl ...
- The 2013 ACM-ICPC Asia Changsha Regional Contest - J
Josephina and RPG Time Limit: 2 Seconds Memory Limit: 65536 KB Special Judge A role-playin ...
- The 2013 ACM-ICPC Asia Changsha Regional Contest - A
Alice's Print Service Time Limit: 2 Seconds Memory Limit: 65536 KB Alice is providing print ser ...
- 2013 ACM/ICPC Asia Regional Chengdu Online---1003
哈哈哈 #include <iostream> #include <cstring> #include <string> #include <cstdio&g ...
- 2013 ACM/ICPC Asia Regional Chengdu Online hdu4731 Minimum palindrome
Minimum palindrome Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Other ...
- HDU4734——2013 ACM/ICPC Asia Regional Chengdu Online
今天做的比赛,和队友都有轻微被虐的赶脚. 诶,我做的题就是这个题目了. 题目描述就是对于一个十进制数数位上的每一位当做一个二进制位来求出这个数,这个定义为G(x). 题目给定你A和B,求在0-B范围内 ...
- HDU 4729 An Easy Problem for Elfness（主席树）（2013 ACM/ICPC Asia Regional Chengdu Online）
Problem Description Pfctgeorge is totally a tall rich and handsome guy. He plans to build a huge wat ...
随机推荐
- js跨域访问，No ‘Access-Control-Allow-Origin‘ header is present on
在本地用ajax跨域访问请求时报错: XMLHttpRequest cannot loadhttp://www.zjblogs.com/. No 'Access-Control-Allow-Origi ...
- SSH自动断开连接的原因
方法一: 用putty/SecureCRT连续3分钟左右没有输入, 就自动断开, 然后必须重新登陆, 很麻烦. 在网上查了很多资料, 发现原因有多种, 环境变量TMOUT引起,ClientAliveC ...
- centos 6.5常见lib库安装
在CentOS安装软件的时候,可能缺少一部分支持库,而报错.这里首先安装系统常用的支持库.那么在安装的时候就会减少很多的错误的出现. # yum install -y gcc gdb strace g ...
- runtime——消息机制
本文授权转载,作者:Sindri的小巢(简书) 从异常说起 我们都知道,在iOS中存在这么一个通用类类型id,它可以用来表示任何对象的类型 —— 这意味着我们使用id类型的对象调用任何一个方法,编译器 ...
- [Eclispe] NDK内建include路径修改
[Eclispe] NDK内建include路径修改 编辑 jni/android.mk 中 LOCAL_C_INCLUDES 变量后,该变量值将被列入项目属性的内建include头文件包含路径,无法 ...
- Flexigrid的API
基本设定 width table的长度(default:auto) height table的宽度(default:200) striped 表格的线的表示(default:true) nov ...
- 异步加载AsyncTask
private void huodeshuju() { new AsyncTask<String, Void, String>() { @Overrid ...
- XListview的下拉刷新、上拉加载、用Pull解析XML
做之前需要导入XListview的文件,此是用第三方的xListview实现的,东西没写全.此是在Fragment中实现的 //--------------XListView的布局---------- ...
- 河南多校大一训练赛 D
题目链接:http://acm.hust.edu.cn/vjudge/contest/125004#problem/D 密码:acm Description If an integer is not ...
- CodeForces 678A Johny Likes Numbers
简单题. #include<cstdio> #include<cstring> #include<cmath> #include<algorithm> ...