hdu GuGuFishtion 6390 数论 欧拉函数
题目:http://acm.hdu.edu.cn/showproblem.php?pid=6390
直接开始证明:
我们设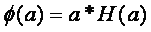 …………………………………….....…...............……………...(1)
…………………………………….....…...............……………...(1)
则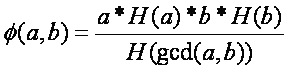 …................................….…(2)
…................................….…(2)
为什么是这样呢,因为我们知道
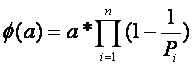
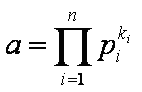
同理得到b的分解和的分解
我们会发现,虽然a和b的分解里可以有相等的部分,但是在里的也就是我们假设为的部分是不会有重复的,那么要由*得出也就是要去除重复部分,的重复部分就是a的和b的的重复部分;那么因为都是乘法,相同的部分就是最大公约数(因为每个都是素数也就是如果a和b的分解没有相同的数那么gcd(, )是不会大于1的);
由此我们开始继续对(2)的后续推论。
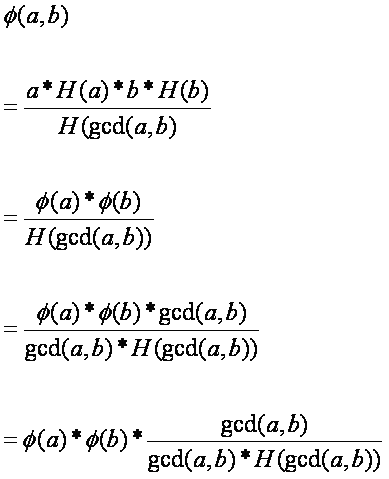
我先设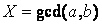 ,那么
,那么
也就是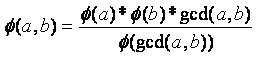
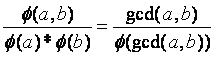 (看了很多博客,就给了个易得,虽然说确实很简单但是对于我这个菜鸡就不友好了)
(看了很多博客,就给了个易得,虽然说确实很简单但是对于我这个菜鸡就不友好了)
这一部分的证明是看了这个大佬的博客的:http://www.cnblogs.com/H-Riven/p/9494391.html
(再提供给同样是数论萌新的人一篇文库【有需要的话】:https://wenku.baidu.com/view/542961fdba0d4a7302763ad5.html)
设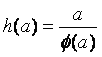
设 (即在
(即在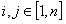 的情况下
的情况下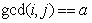 的数量)
的数量)
那么我们实际上就是要求: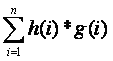 ,对于
,对于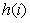 我们可以预处理得到。但是
我们可以预处理得到。但是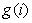 就没那么容易得到了;
就没那么容易得到了;
现在题目就变成求对于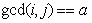 ,在
,在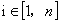 、
、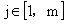 的情况下有多少种方案;
的情况下有多少种方案;
这里我设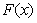 为
为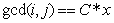 的数量 (C*x表示x的倍数);即可以和HDU1695一样得到
的数量 (C*x表示x的倍数);即可以和HDU1695一样得到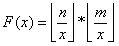 的结论
的结论
设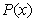 为
为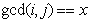 的数量
的数量
那么:
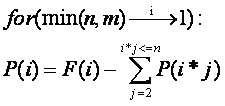
倒过来求的原因是因为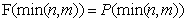 ,也就是我们可以知道最后一位的准确值,那么反过来就可以推到每个位置准确值了;
,也就是我们可以知道最后一位的准确值,那么反过来就可以推到每个位置准确值了;
那么答案就已经出来了;又因为要求的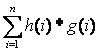 ,对于每个
,对于每个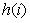 ,是含有有除法的,所以这里要用除法逆元,因为每次的mod都是不同的,所以说每次都要得到逆元,因为
,是含有有除法的,所以这里要用除法逆元,因为每次的mod都是不同的,所以说每次都要得到逆元,因为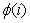 一定会小于min(n,m);所以说每次打从1到 min(n,m)的表比单个值的计算快;
一定会小于min(n,m);所以说每次打从1到 min(n,m)的表比单个值的计算快;
以下是代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e6+;
ll euler[N], inv[N]={, }, F[N], P[N], n, m, mod, mins;
void Euler(){///打欧拉表
register int i, j;
for(i=; i<N; ++i){ euler[i]=i; }
for(i=; i<N; ++i){
if(euler[i]==i){
for(j=i; j<N; j+=i)
euler[j]=euler[j]-euler[j]/i;
}
}
}
void Inv(){///打表求逆元
for(register int i=; i<=mins; ++i){
inv[i]=(ll)(mod-mod/i)*inv[mod%i]%mod;
}
}
int main( ){
Euler();
int T;
register ll ans;
register int i, j;
scanf("%d", &T);
while(T--){
scanf("%I64d%I64d%I64d", &n, &m, &mod);
mins=min(n, m);
Inv();
for(i=; i<=mins; ++i){
F[i]=(n/i)*(m/i)%mod;
}
for(i=mins; i>=; --i){
P[i]=F[i];
for(j=; j*i<=mins; ++j){
P[i]-=P[i*j];
if(P[i]<){
P[i]+=mod;
}
}
}
ans=;
for(i=; i<=mins; ++i){
ans=(ans+(i*inv[euler[i]]%mod)*P[i]%mod)%mod;
}
printf("%I64d\n", ans);
}
}
拙劣的代码
hdu GuGuFishtion 6390 数论 欧拉函数的更多相关文章
- 数论-欧拉函数-LightOJ - 1370
我是知道φ(n)=n-1,n为质数 的,然后给的样例在纸上一算,嗯,好像是找往上最近的质数就行了,而且有些合数的欧拉函数值还会比比它小一点的质数的欧拉函数值要小,所以坚定了往上找最近的质数的决心—— ...
- 【poj 3090】Visible Lattice Points(数论--欧拉函数 找规律求前缀和)
题意:问从(0,0)到(x,y)(0≤x, y≤N)的线段没有与其他整数点相交的点数. 解法:只有 gcd(x,y)=1 时才满足条件,问 N 以前所有的合法点的和,就发现和上一题-- [poj 24 ...
- GuGuFishtion HDU - 6390 (欧拉函数,容斥)
GuGuFishtion \[ Time Limit: 1500 ms\quad Memory Limit: 65536 kB \] 题意 给出定义\(Gu(a, b) = \frac{\phi(ab ...
- HDU 1695 GCD (欧拉函数+容斥原理)
GCD Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submiss ...
- BZOJ-2190 仪仗队 数论+欧拉函数(线性筛)
今天zky学长讲数论,上午水,舒爽的不行..后来下午直接while(true){懵逼:}死循全程懵逼....(可怕)Thinking Bear. 2190: [SDOI2008]仪仗队 Time Li ...
- HDU 5430 Reflect(欧拉函数)
题目: http://acm.hdu.edu.cn/showproblem.php?pid=5430 从镜面材质的圆上一点发出一道光线反射NNN次后首次回到起点. 问本质不同的发射的方案数. 输入描述 ...
- hdu 5279 Reflect phi 欧拉函数
Reflect Time Limit: 1 Sec Memory Limit: 256 MB 题目连接 http://bestcoder.hdu.edu.cn/contests/contest_chi ...
- HDU 1695 GCD(欧拉函数+容斥原理)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1695 题意:x位于区间[a, b],y位于区间[c, d],求满足GCD(x, y) = k的(x, ...
- Codeforces_776E: The Holmes Children (数论 欧拉函数)
题目链接 先看题目中给的函数f(n)和g(n) 对于f(n),若自然数对(x,y)满足 x+y=n,且gcd(x,y)=1,则这样的数对对数为f(n) 证明f(n)=phi(n) 设有命题 对任意自然 ...
随机推荐
- Scrum Meeting NO.4
Scrum Meeting No.4 1.会议内容 今天我们开始着手重构前端通讯模块的代码.用封装性较好的HttpClient代替了源代码中比较底层的访问方式,并按照约定的json格式处理HttpRe ...
- 第三周作业:Visual Studio 2013
在装Visual Studio 2013的时候,提示我升级我的电脑,不然不给安装,于是我就各种升级,完事之后有了这个: 在我耐心的等待之下终于等到安装完成: 我就建立一个新的项目: 我就写了一个简单程 ...
- sql两个日期之间的查询统计
sql查询统计 sql语句: select count(code) as '统计',create_time as '订单时间' from sp_orders where datediff(create ...
- [2017BUAA软工]提问回顾
原博客链接 原问题1:有没有系统的方法来提高一开始的文档的设计后的质量呢 在之前的OO课程上,我已经深刻领会到了设计的重要性,而且在这次的团队开发中,我也是负责从需求分析到代码设计的转换,所以对设计这 ...
- 组件 -- Badge
.badge :长方形的徽章 badge的颜色: .badge-primary .badge-secondary .badge-success .badge-warning ... ... .badg ...
- Docker(二十五)-Docker Machine
Docker Machine 是什么? Docker Machine 是 Docker 官方提供的一个工具,它可以帮助我们在远程的机器上安装 Docker,或者在虚拟机 host 上直接安装虚拟机并在 ...
- Docker(六)-Dcoker仓库
仓库 一个容易混淆的概念是注册服务器(Registry). 实际上注册服务器是管理仓库的具体服务器,每个服务器上可以有多个仓库,而每个仓库下面有多个镜像.从这方面来说, 仓库可以被认为是一个具体的项目 ...
- [财务知识] debt debit credit 的区别于联系
https://blog.csdn.net/sjpljr/article/details/70169303 剑桥词典解释分别为: Debt [C or U ] n.something, especia ...
- MySQL基础(二):视图、触发器、函数、事务、存储过程
一.视图 视图是一个虚拟表(非真实存在),其本质是[根据SQL语句获取动态的数据集,并为其命名],用户使用时只需使用[名称]即可获取结果集,并可以将其当作表来使用. 视图和上一篇学到的临时表搜索类似. ...
- java自定义注解学习(三)_注解解析及应用
上篇文章已经介绍了注解的基本构成信息.这篇文章,主要介绍注解的解析.毕竟你只声明了注解,是没有用的.需要进行解析.主要就是利用反射机制在运行时进行查看和利用这些信息 常用方法汇总 在Class.Fie ...
