C#Winform将WebBowser控件替换为Chrome内核

摘要

　　由于最近要做一个浏览器式的软件，其中有不少地方需要使用到jQuery和BootStrap，但是在C#中，默认的WebBrowser控件默认使用的是IE的core，而低版本的IE在JS加载上总是容易有问题，因此，打算使用Chrome的内核替换IE。

准备工作

　　首先，你要明白Chrome浏览器的内核不叫Chrome，而是Webkit，因此，我们只要找到Webkit的项目就好了。

　　1.下载WebKit的项目bin,网址如下：

　　https://sourceforge.net/projects/webkitdotnet/files/WebKit%20.NET%200.x/0.5/WebKit.NET-0.5-bin-cairo.zip/download。

　　2.下载解压后的目录结构如下：

　　

　　3.将bin文件夹下的所有（没错！是所有文件复制），并粘贴到项目文件夹下，目标目录是：项目名/bin/Debug/

　　

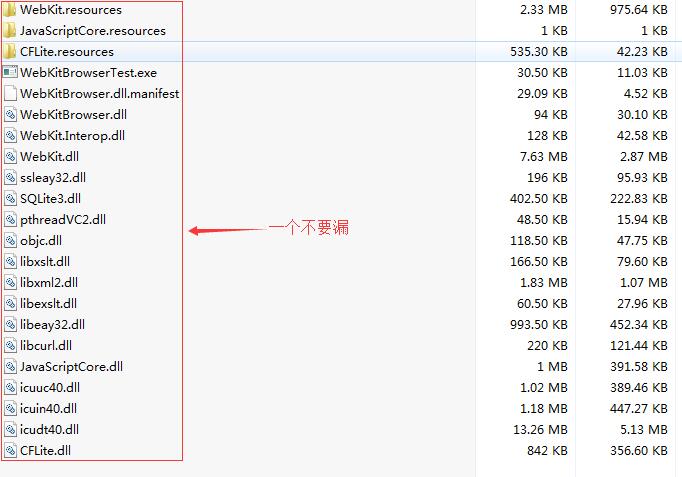
　　4.导入Webkitbrowser的dll到你的项目中。在VS2015的操作如下（其他的类推）：

　　　在Solution Explorer下，选中你的项目名，然后右键，选择Add，然后选择Reference，如下图：

　　

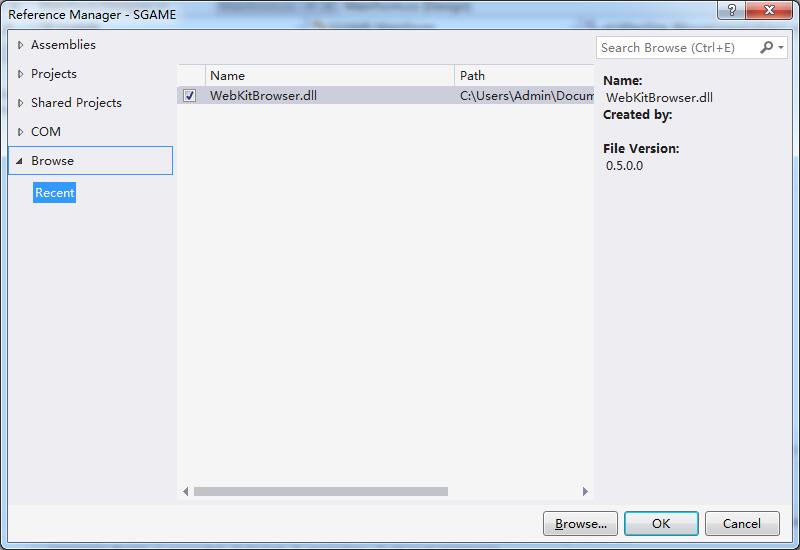
　　5.在弹出的对话框里。选择Browse -> Browse...，然后选择你的：项目名/bin/Debug下之前粘贴的WebKitBrowser.dll导入，结果如下图：

　　

编码阶段

　　1.你要做的，首先选择你之前下载的bin目录下的WebKitBrowser.dll，然后复制，如下图：

　　

　　2.在C#的控件栏中，自己建一个自定义的C#控件栏，例如我的叫WebBrowser,然后在工具栏中粘贴刚才复制的dll,最后效果如下图：

　　

　　之后你就可以正常使用WebKitBrowser控件了。

　　3.大功告成了，通过这个网站可以测试浏览器的内核，网址:http://ie.icoa.cn/

　　至于运行代码，如下给出：

1 private void Form1_Load(object sender, EventArgs e)
2 {
3     webKitBrowser1.Navigate("http://ie.icoa.cn/");
4 }

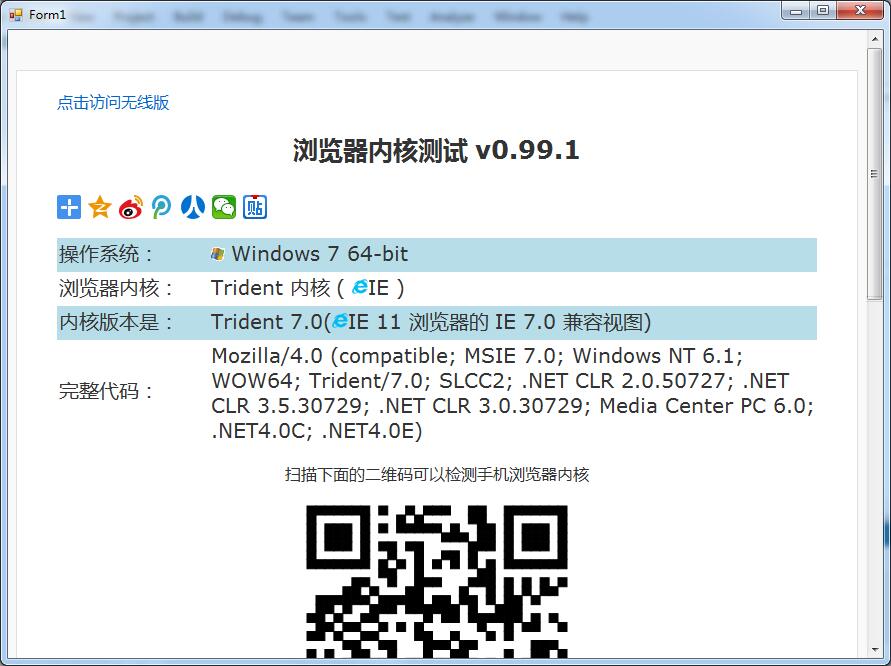
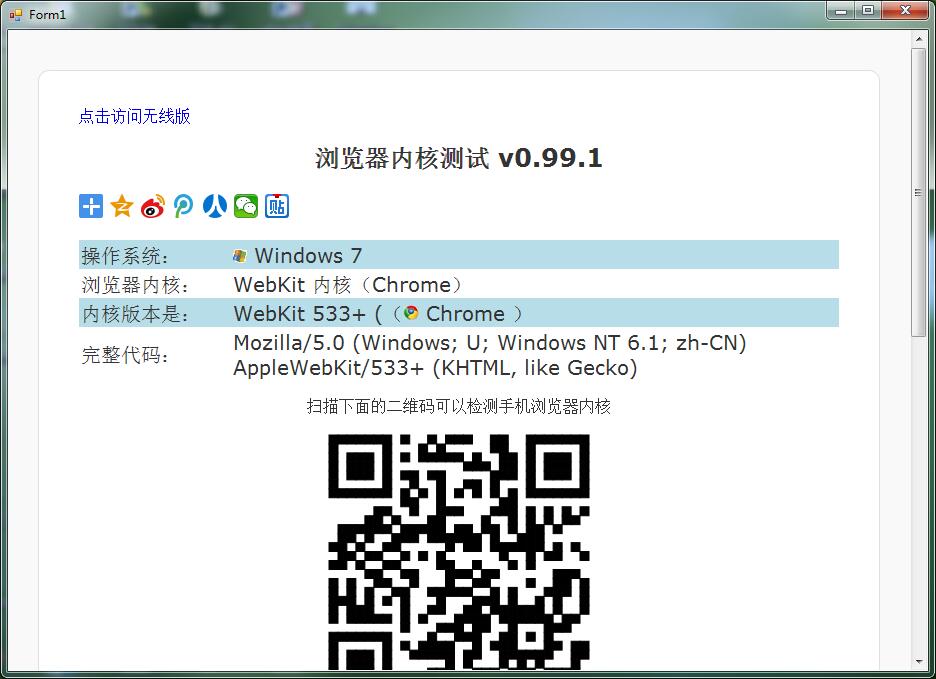
　　下面是配置前和配置后的对比：

　　配置前：

　　

　　配置后：

　　

致谢

　　感谢s_p评论中指出的问题，另外如果你想制作Release版而不是Debug的，你存放的目录应该是：项目名/bin/release。

补充

　　感谢园友的指出，WebKitBrowser这个项目目前已经不维护了，随着.Net版本的提升，也很有可能会出现问题，因此推荐另一个比较好用的CefSharp，具体流程和WebKitBrowser基本一致。

　　如果有园友想用CefSharp，欢迎查看这篇文章，讲的很详细，来自codeceo：传送门在这里:)