Meshgrid函数的基本用法(转载)

在Numpy的官方文章里，meshgrid函数的英文描述也显得文绉绉的，理解起来有些难度。

可以这么理解，meshgrid函数用两个坐标轴上的点在平面上画网格。

用法：

　　[X,Y]=meshgrid(x,y)

　　[X,Y]=meshgrid(x)与[X,Y]=meshgrid(x,x)是等同的

　　[X,Y,Z]=meshgrid(x,y,z)生成三维数组，可用来计算三变量的函数和绘制三维立体图

这里，主要以[X,Y]=meshgrid(x,y)为例，来对该函数进行介绍。

[X,Y] = meshgrid(x,y) 将向量x和y定义的区域转换成矩阵X和Y,其中矩阵X的行向量是向量x的简单复制，而矩阵Y的列向量是向量y的简单复制(注：下面代码中X和Y均是数组，在文中统一称为矩阵了)。

假设x是长度为m的向量，y是长度为n的向量，则最终生成的矩阵X和Y的维度都是 nm （注意不是mn）。

文字描述可能不是太好理解，下面通过代码演示下：

加载数据

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
m, n = (5, 3)
x = np.linspace(0, 1, m)
y = np.linspace(0, 1, n)
X, Y = np.meshgrid(x,y)

查看向量x和向量y

x
out:
array([ 0. , 0.25, 0.5 , 0.75, 1. ])
y
out:
array([ 0. , 0.5, 1. ])

查看矩阵X和矩阵Y

X
out:
array([[ 0. , 0.25, 0.5 , 0.75, 1. ],
[ 0. , 0.25, 0.5 , 0.75, 1. ],
[ 0. , 0.25, 0.5 , 0.75, 1. ]])
Y
out:
array([[ 0. , 0. , 0. , 0. , 0. ],
[ 0.5, 0.5, 0.5, 0.5, 0.5],
[ 1. , 1. , 1. , 1. , 1. ]])

查看矩阵对应的维度

X.shape
out:
(3, 5)
Y.shape
out:
(3, 5)

meshgrid函数的运行过程，可以通过下面的示意图来加深理解：

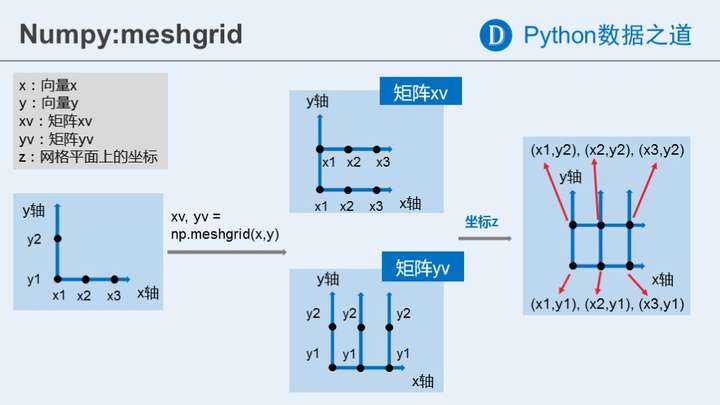
再者，也可以通过在matplotlib中进行可视化，来查看函数运行后得到的网格化数据的结果

plt.plot(X, Y, marker='.', color='blue', linestyle='none')
plt.show()

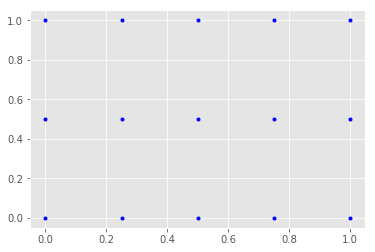
当然，我们也可以获得网格平面上坐标点的数据，如下：

z = [i for i in zip(X.flat,Y.flat)]
z
out:
[(0.0, 0.0),
(0.25, 0.0),
(0.5, 0.0),
(0.75, 0.0),
(1.0, 0.0),
(0.0, 0.5),
(0.25, 0.5),
(0.5, 0.5),
(0.75, 0.5),
(1.0, 0.5),
(0.0, 1.0),
(0.25, 1.0),
(0.5, 1.0),
(0.75, 1.0),
(1.0, 1.0)]

Meshgrid函数的一些应用场景

Meshgrid函数常用的场景有等高线绘制及机器学习中SVC超平面的绘制（二维场景下）。

分别图示如下：

（1）等高线

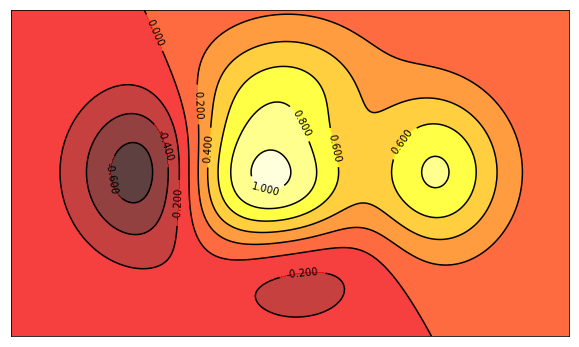
（2）SVC中超平面的绘制：

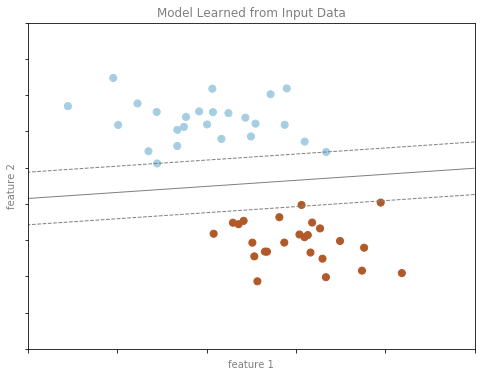
原博地址：https://zhuanlan.zhihu.com/p/29663486