李群与李代数在slam中的应用
昨天,刚接触道了李群和李代数,查了许多资料,也看了一些视屏。今天来谈谈自己的感受。
李群是有一个挪威数学家提出的,在十九二十世纪得到了很大的发展。
其归于非组合数学,现在简单介绍李群和李代数的概念。群的定义是一种集合加上一种运算的代数结构。其集合记为A,运算记为 . ,当其满足以下四条性质时,就称其为(A,.)群。

为了大家更好的理解,我还是放上讲师(高博slam十四讲其四)的ppt吧。


















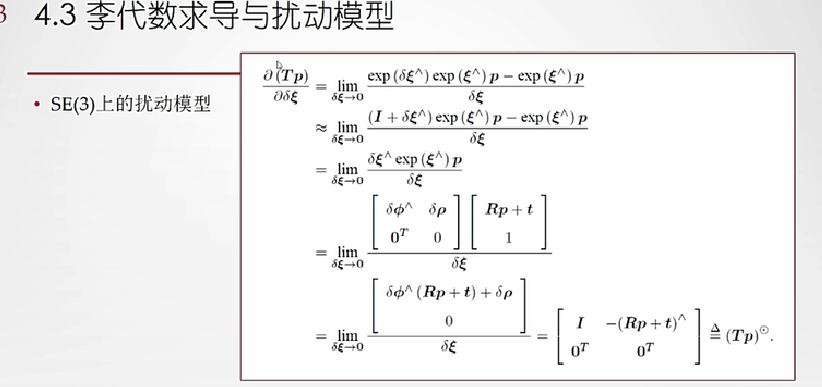
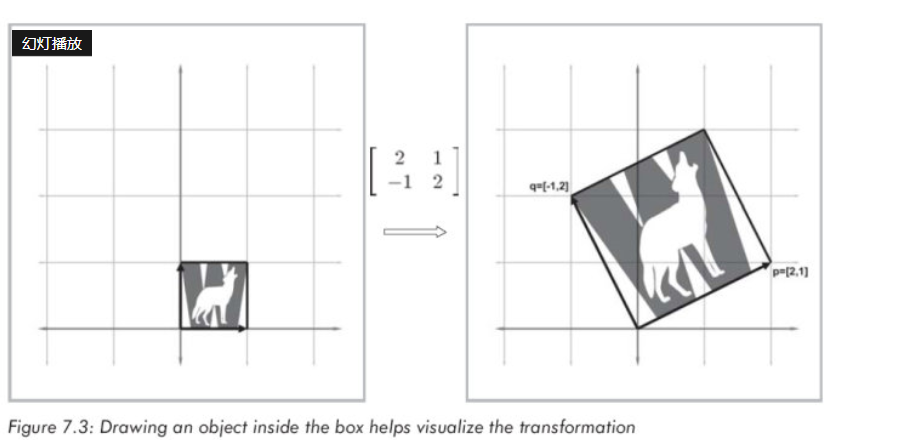
矩阵旋转
李群与李代数在slam中的应用的更多相关文章
- 视觉SLAM中的数学基础 第四篇 李群与李代数(2)
前言 理解李群与李代数,是理解许多SLAM中关键问题的基础.本讲我们继续介绍李群李代数的相关知识,重点放在李群李代数的微积分上,这对解决姿态估计问题具有重要意义. 回顾 为了描述三维空间里的运动,我们 ...
- 视觉SLAM中的数学基础 第三篇 李群与李代数
视觉SLAM中的数学基础 第三篇 李群与李代数 前言 在SLAM中,除了表达3D旋转与位移之外,我们还要对它们进行估计,因为SLAM整个过程就是在不断地估计机器人的位姿与地图.为了做这件事,需要对变换 ...
- 从零开始一起学习SLAM | 为啥需要李群与李代数?
很多刚刚接触SLAM的小伙伴在看到李群和李代数这部分的时候,都有点蒙蒙哒,感觉突然到了另外一个世界,很多都不自觉的跳过了,但是这里必须强调一点,这部分在后续SLAM的学习中其实是非常重要的基础,不信你 ...
- SLAM中的EKF,UKF,PF原理简介
这是我在知乎上问题写的答案,修改了一下排版,转到博客里. 原问题: 能否简单并且易懂地介绍一下多个基于滤波方法的SLAM算法原理? 目前SLAM后端都开始用优化的方法来做,题主想要了解一下之前基于 ...
- SLAM中的优化理论(一)—— 线性最小二乘
最近想写一篇系列博客比较系统的解释一下 SLAM 中运用到的优化理论相关内容,包括线性最小二乘.非线性最小二乘.最小二乘工具的使用.最大似然与最小二 乘的关系以及矩阵的稀疏性等内容.一方面是督促自己对 ...
- SLAM中的优化理论(二)- 非线性最小二乘
本篇博客为系列博客第二篇,主要介绍非线性最小二乘相关内容,线性最小二乘介绍请参见SLAM中的优化理论(一)-- 线性最小二乘.本篇博客期望通过下降法和信任区域法引出高斯牛顿和LM两种常用的非线性优化方 ...
- 视觉SLAM中相机详解
视觉SLAM中,通常是指使用相机来解决定位和建图问题. SLAM中使用的相机往往更加简单,不携带昂贵的镜头,以一定的速率拍摄周围的环境,形成一个连续的视频流. 相机分类: 单目相机:只是用一个摄像头进 ...
- SLAM中的变换(旋转与位移)表示方法
1.旋转矩阵 注:旋转矩阵标题下涉及到的SLAM均不包含位移. 根据同一点P在不同坐标系下e(e1,e2,e3)e'(e1',e2',e3')的坐标a(a1,a2,a3)a'(a1',a2',a3') ...
- 视觉SLAM中的数学基础 第二篇 四元数
视觉SLAM中的数学基础 第二篇 四元数 什么是四元数 相比欧拉角,四元数(Quaternion)则是一种紧凑.易于迭代.又不会出现奇异值的表示方法.它在程序中广为使用,例如ROS和几个著名的SLAM ...
随机推荐
- jQuery validate插件,自动验证无效的原因及解决方法归纳
最近在使用validate插件进行验证的时候,出现有的控件在个别事件(比如keydown.foucs.onchange等)下不能自动验证,而有的控件却又正常,当时觉得很诡异,后来仔细测试查看,归纳原因 ...
- nmcli 命令使用
nmcli 是 NetworkManager 的控制客户端,通过 man 查看可知: NMCLI(1) General Commands Manual NMCLI(1) NAME nmcli - co ...
- orcl创建表及管理表
常用的字段数据类型: .字符串(varchar2(n)) n表示保存最大长度,基本200作用..整数(number(n)) n位的整数,也可用int代替.小数(number(n,m)) m为小数位,n ...
- CentOS7中部署Showdoc
目录 CentOS7中部署Showdoc 前置环境 部署 配置文件 解压安装包 添加启动服务 设置权限 运行安装 界面 CentOS7中部署Showdoc 文:铁乐与猫 前置环境 因为showdoc其 ...
- Office 手动kms激活方法
服务作用:在线激活windows和office 适用对象:VOL版本的windows和office 适用版本:截止到win10和office2016的所有版本 服务时间:24H,偶尔更新维护 优点:在 ...
- arm 开发板更新 gcc/gcc++ | Debain 更新 gcc,无需编译直接更新 gcc
4我的板子是 Orange pi 3,只能以 卧槽来形容... 我是搞.net core的,这板子死活搞不了. 刷的是Debain系统. 说实话,这个板子不错,可就是官方的系统实在不敢恭维,内核旧,软 ...
- 更改win系统的鼠标样式
一.找一个你心仪的鼠标样式(.cur文件),并放到 C:\Windows\Cursors 目录下 二.打开,控制面板 -> 硬件和声音 -> 鼠标 ,如下图: 三.浏览鼠标目录,找到你存放 ...
- PyQt5--MainWindow
# -*- coding:utf-8 -*- ''' Created on Sep 14, 2018 @author: SaShuangYiBing ''' import sys from PyQt5 ...
- 死磕nginx系列--nginx 限流配置
限流算法 令牌桶算法 算法思想是: 令牌以固定速率产生,并缓存到令牌桶中: 令牌桶放满时,多余的令牌被丢弃: 请求要消耗等比例的令牌才能被处理: 令牌不够时,请求被缓存. 漏桶算法 算法思想是: 水( ...
- The Rock Game
Before the cows head home for rest and recreation, Farmer John wantsthem to get some intellectual st ...
