课程一(Neural Networks and Deep Learning)，第二周（Basics of Neural Network programming）—— 1、10个测验题（Neural Network Basics）

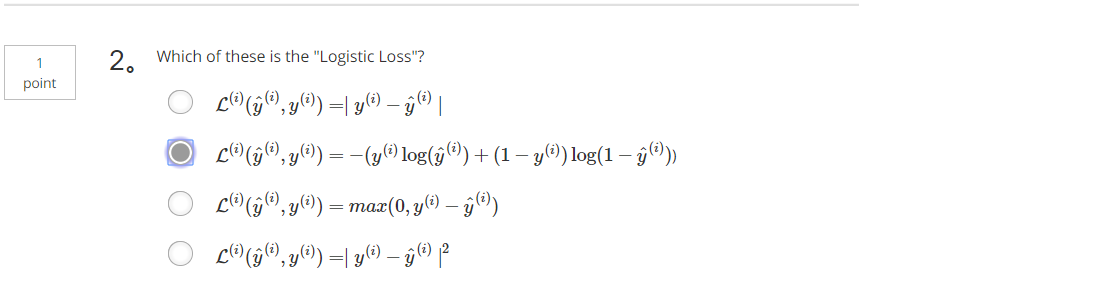
--------------------------------------------------中文翻译-----------------------------------------------------------------------------------------

1、神经元的计算是什么？(B)

A. 在将输出应用到激活函数之前, 神经元计算所有特征的平均值

B. 神经元计算一个线性函数 (z = Wx + b), 然后是一个激活函数

C. 神经元计算一个激活函数, 后跟一个线性函数 (z = Wx + b)

D. 一个神经元计算一个函数 g, 它将输入 x 线性地缩放 (Wx + b)

2、下面哪个是损失函数？（B）

见对应的英文题2

3、假设 img 是一个 (32，32，3) 数组, 代表一个32x32 的图像与3色通道红色, 绿色和蓝色。如何将其重塑为列向量？(B)

A. x = img 重塑 (32 * 32,3))

B. x = img 重塑 (32 * 32 * 3,1))

C. x = img 重塑 (1,32 * 32, * 3))

D. x = img 重塑 (3,32 * 32))

 

4、考虑以下两个随机数组 "a" 和 "b"， "c" 的形状是什么？（B）

a = np.random.randn(2, 3) # a.shape = (2, 3)
b = np.random.randn(2, 1) # b.shape = (2, 1)
c = a + b

A. c.shape = (2, 1)

B. c.shape = (2, 3)

C. c.shape = (3, 2)

D. 由于大小不匹配, 无法进行计算。这将是 "错误"!

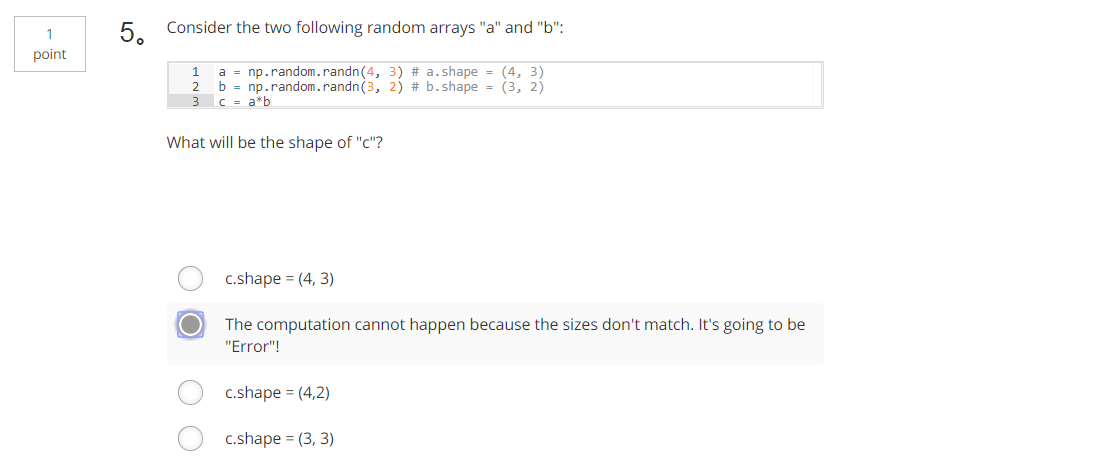
5、考虑以下两个随机数组 "a" 和 "b"， "c" 的形状是什么？（A）

a = np.random.randn(4, 3) # a.shape = (4, 3)
b = np.random.randn(3, 2) # b.shape = (3, 2)
c = a*b

A. 由于大小不匹配, 无法进行计算。这将是 "错误"!

A. c.shape = (3, 3)

B. c.shape = (4, 2)

C. c.shape = (4, 3)

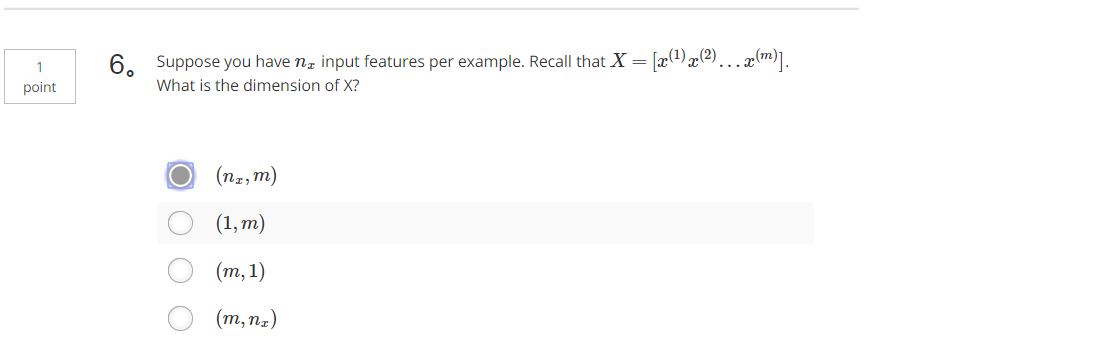
6、假设每一个样本的特征为n_x维，X=[x⁽¹⁾x⁽²⁾...x^(m)]，X的维度是多少？(A)

A. (n_x,m)

B. (1,m)

C. (m,1)

D. (m,n_x)

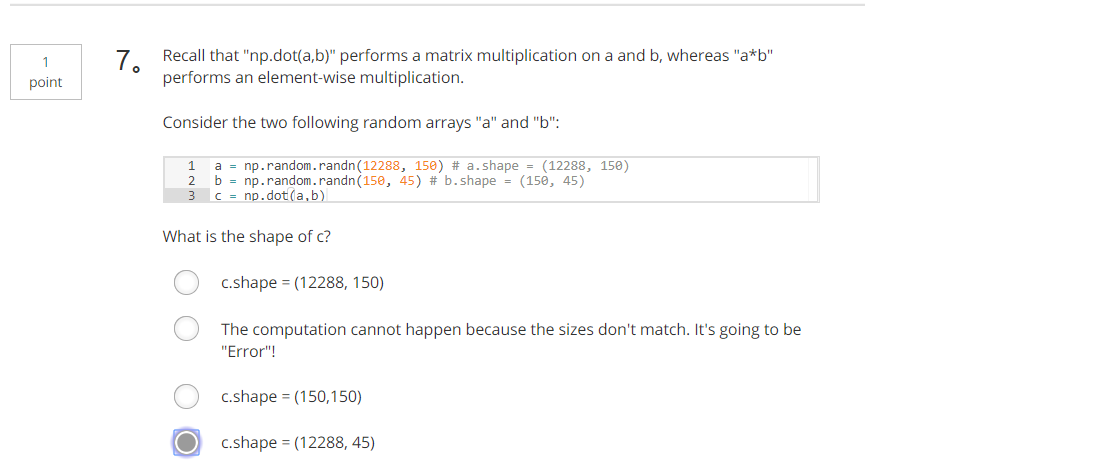
7、记得 "np. dot(a, b)" 在 a 和 b 上执行矩阵乘法, 而 "a * b" 执行元素乘法。考虑以下两个随机数组 "a" 和 "b":

a = np.random.randn(12288, 150) # a.shape = (12288, 150)
b = np.random.randn(150, 45) # b.shape = (150, 45)
c = np.dot(a,b)

c 的形状是什么？(D)

A. c. 形状 = (12288, 150)

B. 由于大小不匹配, 无法进行计算。这将是 "错误"!

C. c. 形状 = (150150)

D. c. 形状 = (12288, 45)

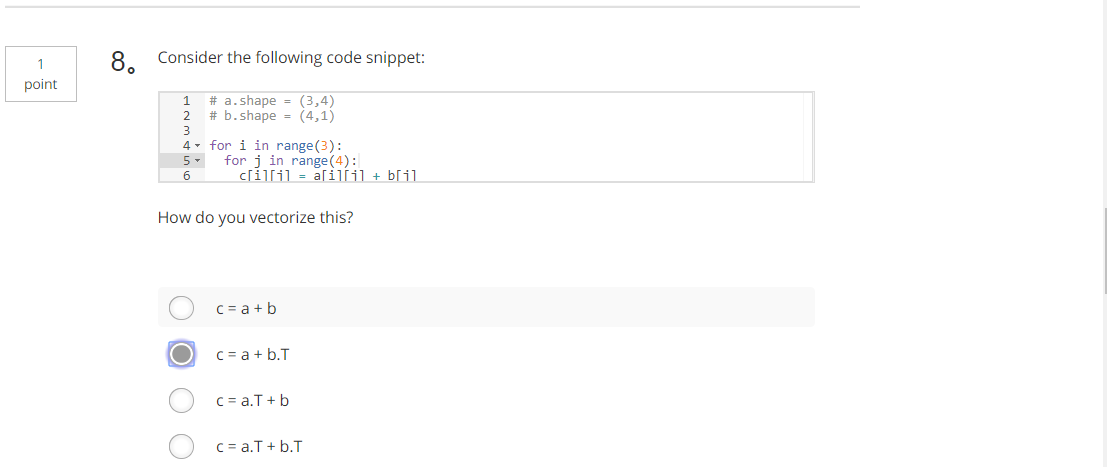
8、请考虑以下代码段，你怎么量化？（B）

# a.shape = (3,4)
# b.shape = (4,1)

for i in range(3):
  for j in range(4):
    c[i][j] = a[i][j] + b[j]

A. c = a + b

B. c = a + b.T

C. c = a.T + b

D. c = a.T + b.T

9、请考虑以下代码：c的结果？(如果您不确定, 请随时在 python 中运行此查找)。(A)

a = np.random.randn(3, 3)
b = np.random.randn(3, 1)
c = a*b

A. 这将触发广播机制, 所以 b 被复制三次，成为 (3，3), * 代表矩阵对应元素相乘, 所以 c 的大小将是 (3, 3)

B. 这将触发广播机制, 所以 b 被复制三次，成为 (3, 3), * 代表矩阵乘法，运算两个3x3 的矩阵, 所以 c的大小将是 (3, 3)

C. 这将乘以一个3x3 矩阵 a 与一个3x1 向量b, 从而得到一个3x1 向量。即, c的大小 (3，1)。

D. 这将导致错误, 因为您不能使用 "*" 来操作这两个矩阵。你需要改用 np.dot(a, b)

 

10、考虑下面的计算图。什么是输出 J？（B） （注：由于网站无法显示图片，这题答案不确定。考察的知识点是计算图）

 

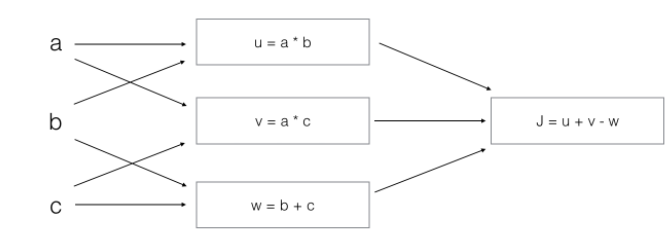
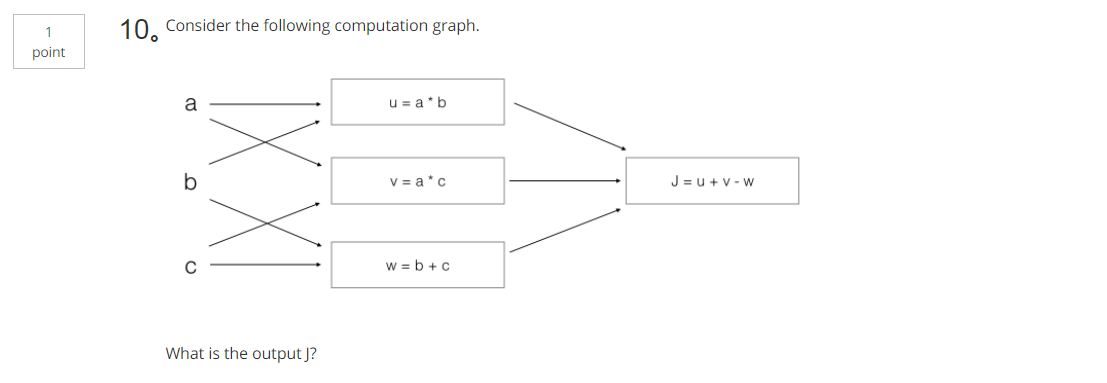
A. J = (c - 1)*(b + a)

B. J = (a - 1) * (b + c)

C. J = a*b + b*c + a*c

D. J = (b - 1) * (c + a)