[软工课程博客] 求解第N个素数

任务

求解第 10,0000、100,0000、1000,0000 ... 个素数（要求精确解）。

想法

Sieve of Eratosthenes

学习初等数论的时候曾经学过埃拉托斯特尼筛法(Sieve of Eratosthenes)，这是一种非常古老但是非常有效的求解$p_n$的方法，其原理非常简单：从2开始，将每个素数的各个倍数都标记成合数。

其原理如下图所示：

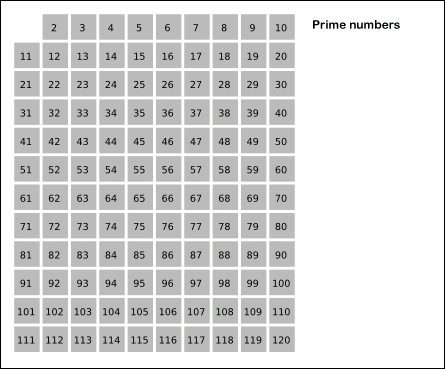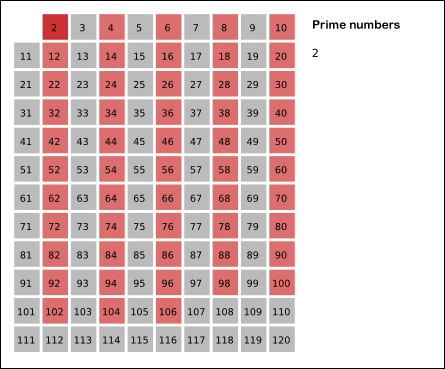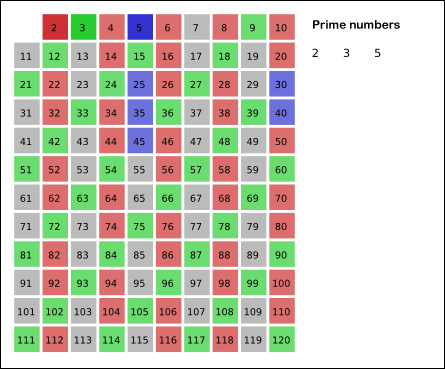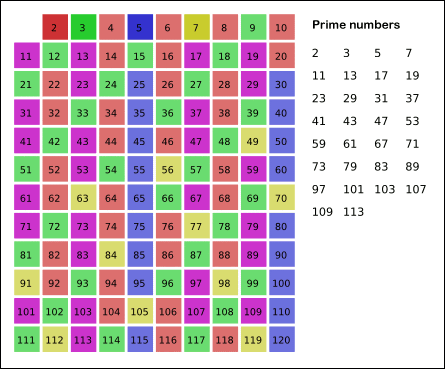图引自维基百科

埃拉托斯特尼筛法相比于传统试除法最大的优势在于：筛法是将素数的各个倍数标记成合数，而非判定每个素数是否是素数的倍数，使用了加法代替了除法，降低了时间复杂度。

举个简单的例子，已知2、3、5、7是素数，求小于49的其余素数。

试除法

对于每一个数$m ( 7 < m < 49 )$而言，都要进行如下判定：

求出 ${\lceil}\sqrt{m}{\rceil} + 1 = n$ ，试除 $ n $以内的素数即可判定 $ m $是否为素数。
m / 2 ... 不整除。
m / 3 ... 不整除。
...

对于m而言，只有两种情况可以结束试除：

m 是素数，要把所有候选素数都试除一遍。
m 是合数，可以被某个素数整除。

对于试除法而言，假设新找到 x 个素数， y 个合数，需要试除的素数因子有 m 个，则至少需要做 $ x * m + y $次除法。

埃拉托斯特尼筛法

2，2 + 2 = 4, 4 + 2 = 6 ... 48 + 2 = 50 > 49，下一个。
3，3 + 3 = 6, 6 + 3 = 9 ... 48 + 3 = 51 > 49，下一个。
5，5 + 5 = 10, 10 + 5 = 15 ... 45 + 5 = 50 > 49，下一个。
7, 7 + 7 = 14, 14 + 7 = 21 ... 42 + 7 = 49 = 49，下一个。
没有小于 8 的素数了，停止标记，没有标记到的都是素数。

实际上，假设在 $\sqrt{x}$ 以内有 $ m $个素数，在 $(\sqrt{x},x]$范围内又找到了 $n $个素数，可以明显看到试除法和筛法的差异：

试除法至少要做 $ n * m + x - n - m (1)$次除法
筛法需要做 $ x - n - m (2)$次加法

做一次除法运算的时间要大于加法，且有 $(1)$ > $(2)$，所以试除法开销远比筛法大。

现在回到问题本身，问题本身是求解第 n 个素数，所以我们一开始并不知道我们需要在多大的范围内求解素数，但是许多数学家给了我们很多定理，比如这个第$n$个素数$p_n$的不等式。

\[p_n < n \ln n + n \ln \ln n\! ( n ≥ 6 )
\]

有了这个函数，我们可以在输入 $ n $之后用它估算第 $ n $个素数的上界，继而求解。

优化一：朴素筛法

输入的 $n$ 值为素数的序号，假设求得的素数上界为 limit。为了让筛法跑得更快，在内存允许的范围内，我们可以直接用一个limit大小的数组 sieve[limit] 求解：下标是int，值为bool，数组初始值均为 true，表示都未标记。假设下标为 index。

index = 2，sieve[index] = true，开始标记，逐次将 sieve[index+2]标记为false，直到下标超过limit。
index = 3，sieve[index] = true，开始标记，逐次将 sieve[index+3]标记为false，直到下标超过limit。
index = 4, sieve[index] = false，跳过。

...

按照上述方式标记完成后，最终在数组中过滤一遍，求得第 n 个未被标记的下标值，即为第 n 个素数。

附代码如下：

public static void Normal_Sieve(int nth)

{

    int startTime = System.Environment.TickCount;

    int limit = nth < 6 ? 25 : (int)(nth * (Math.Log(nth) + Math.Log(Math.Log(nth))));

    int count = 0;

    List<bool> is_prime = new List<bool>(limit+1);

    for (int i = 0; i < limit+1; i++)

        is_prime.Add(true);

    for (int i = 2; i * i <= limit; i++)

        if (is_prime[i])

            for (int j = i * i; j <= limit; j += i)

                is_prime[j] = false;

    for(int i=2;i<is_prime.Count();i++)

    {

        if (is_prime[i])

            count++;

        if(count == nth)

        {

            Console.WriteLine("The nth_prime is:{0} SpentTime:{1}ms",i,Environment.TickCount- startTime);

            break;

        }

    }

}

优化二：位筛法

位筛法相比于简单筛法的改进就是：用1个比特位来标记某个下标是否是素数。1个bool类型要占 8 位，用1个比特位可以使程序在极限内存容量的情况下，比普通筛法能多计算一些素数。

举个例子，按照上面的普通筛法，因为内存大小的限制最多只能求解第 1000,000,000 个素数，那么位筛法就可以求解到第 7000,000,000 个素数。

下面附上位筛法的代码

public static void Bit_Sieve(int nth)

{

    int startTime = Environment.TickCount;

    int limit = nth < 6 ? 25 : (int)(nth * (Math.Log(nth) + Math.Log(Math.Log(nth))));

    int count = 0;

    int total = limit + 1;

    int sqrt = (int)Math.Sqrt(limit) + 1;

    //[31 30 29 ... 0] every number maps to a bit in uint.

    List<uint> is_prime = new List<uint>((total >> 5) + 1);

    for (int i = 0; i < (total >> 5) + 1; i++)

        is_prime.Add(0x0);

    for (int i = 2; i <= sqrt; i++)

        // is_prime[i>>5] bit i % 32 == 0 means it is a prime

        if ((is_prime[i >> 5] & (1 << (i & 31))) == 0)

        {

            for (int j = i * i; j <= total; j += i)

                // is_prime[j>>5] bit j % 32 = 1;

                is_prime[j >> 5] |= (uint)1 << (j & 31);

        }

    for (int i = 2; i < total; i++)

    {

        if ((is_prime[i >> 5] & (1 << (i & 31))) == 0)

        {

            count++;

            if (count == nth)

            {

                Console.WriteLine("The {0}th_prime is:{1} SpentTime:{2}ms",nth , i, Environment.TickCount - startTime);

                break;

            }

        }

    }

}

在位筛法中大部分运算都是移位、与和或的运算，所以在测试时发现要比简单的筛法更快一些。

优化三：局部筛法

假设计算得出的第$n$个素数上界为$x$，在位筛法中，我们申请了一个大小为$x bit$的数组用来标记合数。随之而来一个问题，难道在筛法中，我们必须使用 $x bit$才能求出第 n 个素数吗？

当然不是，对于素数上界$x$，其实不需要这么大的空间，我们只需把$\sqrt{x}$以前的素数保存下来即可。

为什么一定是 $\sqrt{x}$呢？想象一下最暴力的试除法：它在判定一个数是否为素数时，需要遍历试除$\sqrt{x}$及以内的素因子。如果$x$是一个合数，则必然存在一个素因子整除$x$，且其值小于等于$\sqrt{x}$。那么反过来想一下，在筛法中，如果$\sqrt{x}$及以内的所有素因子都没有标记$x$为合数，那么它一定是一个素数了。

基于这样的思想，我们将$[0,\sqrt{x}]$内的素数保存下来，然后对$[\sqrt{x},x]$分段去扫，每扫一段就记录一下本段扫到了多少个素数。这样每次需要载入内存的就只有用于扫描的小素数数组和被扫描的段数组，相比位筛法可以节省更多内存空间。

下面举个简单的例子来说明这种算法：

假设要求解第11个素数(31)，我们估计出上界为 36，然后下面就是局部筛法的求解过程。

$\sqrt{36}=6$，然后利用埃拉托斯特尼筛法求出[2,6]内的素数，即数组 [2,3,5]，此时素数有 3 个。
申请一个大小为10的数组 **A **存储被扫描段。
将[7,36]内的元素按照10个元素一组的方式分成三组（Ps:最后一组不够10个元素）
初始化数组A，此时数组A的下标[0,9]分别映射到[7,16]。
- 用素数2开始标记，因为8、10、12...是2的倍数，所以标记A[1]、A[3]、A[5]...为合数。
- 用素数3开始标记，因为9、12、15...是3的倍数，标记A[2]、A[5]、A[8]...为合数。
- 用素数5开始标记，因为10、15是5的倍数，标记A[3]、A[8]为合数。
- 扫描A数组内未被标记元素下标为：0、4、6、10，所以这一段有 4 个素数，把它们对应的实际数字存入素数数组。
- 现在已经发现了 7 个素数，还未达到预期的11个，继续扫描。
重新初始化数组A，此时数组A的下标[0,9]分别映射到[17,26]。
- 与上述过程一样，用素数2、3、5，分别扫描一遍。
- 记下未被标记的数字，这一段扫描到了 2个素数，到现在已经发现了 9个素数。
重新初始化数组A，继续扫描寻找。

局部筛法的求解过程如上所述，因为每个时刻内存中只需要一个段的内存来存放需要扫描的段，而不需要一次性把所有的段都加载到内存中进行筛选，所以其对内存的要求更低。

下面附上局部筛法的代码

public static void Local_Bit_Sieve(int nth)

{

    int startTime = Environment.TickCount;

    int limit = nth < 6 ? 25 :(int)(nth * (Math.Log(nth) + Math.Log(Math.Log(nth))));

    int sqrt = (int) Math.Sqrt(limit) + 1;

    //Get all primes which are less than \sqrt{limit}

    List<uint> isPrime = new List<uint>((sqrt >> 5) +1);

    for (int i = 0; i < (sqrt >> 5) + 1; i++)

        isPrime.Add(0x0);

    for (int i = 2; i * i <= sqrt; i++)

        // is_prime[i>>5] bit i % 32 == 0 means it is a prime

        if ((isPrime[i >> 5] & (1 << (i & 31))) == 0)

        {

            for (int j = i * i; j <= sqrt; j += i)

                // is_prime[j>>5] bit j % 32 = 1;

                isPrime[j >> 5] |= (uint)1 << (j & 31);

        }

    //smallPrimes store the primes

    List<int> smallPrimes = new List<int>();

    for (int i = 2; i < sqrt; i++)

    {

        if ((isPrime[i >> 5] & (1 << (i & 31))) == 0)

        {

            smallPrimes.Add(i);

        }

    }

    int segSize = Math.Max(sqrt,256 * 256);

    uint[] primeSeg = new uint[segSize];

    //allPrimes store all primes which are found.

    List<int> allPrimes = new List<int>();

    allPrimes.AddRange(smallPrimes);

    int high = segSize << 5;

    //chunk [2,limit] into different segments

    for (int low = sqrt; low <= limit; low += segSize << 5)

    {

        Array.Clear(primeSeg,0,segSize);

        //for each prime, use them to mark the [low,low + segSize]

        foreach (var sPrime in smallPrimes)

        {

            int initValue = low % sPrime;

            for (int i = (initValue == 0 ? initValue : sPrime - initValue); i < high; i += sPrime)

            {

                primeSeg[i >> 5] |= (uint) 1 << (i & 31);

            }

        }

        for (int i = 0; i < high; i++)

        {

            if ((primeSeg[i >> 5] & (1 << (i & 31))) == 0)

                allPrimes.Add(i + low);

        }

        if (allPrimes.Count() > nth)

        {

            Console.WriteLine("The {0}th_prime is:{1} SpentTime:{2}ms",nth, allPrimes[nth-1],

                Environment.TickCount - startTime);

            break;

        }

    }

}

优化四：局部筛法段优化

我们之前之所以说使用朴素筛法可以跑得飞快，是因为从直觉上说，朴素筛法一次性将所有的数据都加载到内存中，一次筛完。而局部筛法却需要筛取多次，筛取多次好像时间开销就要比一次加载筛取要多。

看起来局部筛法好像需要筛多次，所以它所耗费的时间就要比一次筛的要慢，但实际上却不是这样。实际上，计算机系统中Cache的存在对局部筛法更加有利，所耗费的时间也更小。我们分段筛选，反而更加符合空间上的局部性，所以程序可以更高效地利用Cache，Cache的存取速度要远大于内存，所以局部筛法耗费的时间要比朴素筛更少。这个问题可以这么形容：是用一个振动频率比较慢，但是很大的筛子筛选比较快，还是用连续用多个振动频率较快，但是比较小的筛子筛快？

我们可以通过选择一个合理的段大小来减少 Cache miss的概率。我电脑上的L1Cache容量是 256KB，所以最后我选择了 256 * 256 作为段的大小。

Benchmark

n	简单筛法	位筛法	局部位筛法
1,000,000	1.75s	0.938s	0.5s
2,000,000	4.562s	4.328s	2.156s
3,000,000	7.063s	7.140s	3.140s
5,000,000	13.328s	11.407s	4.750s
8,000,000	22.484s	17.110s	9.140s
10,000,000	23.563s	22.347s	11.078s
20,000,000	57.219s	53.313s	22.734s

目前的测试只是大致估计，这个数字不是很准，仅供参考。