NOIP2016-D2-T2 蚯蚓（单调队列）

构建三个单调队列（用STL），分别储存未切的蚯蚓，切后的第一段，切后的第二段，即可简单证明其单调性。

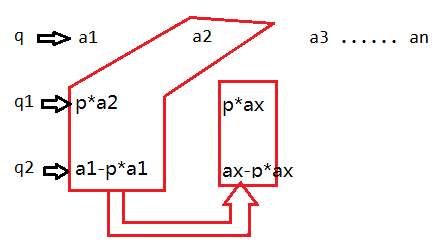
证明：
设$q$为单调队列
$\because a_1 \geqslant a_2 \geqslant a_3 \geqslant \dots \geqslant a_n$
$\therefore a_2\leqslant a_1 ,p\cdot a_1 \leqslant a_1,(a_1-p\cdot a_1)\leqslant a_1$
$又 \because a_x 取自,a_2,(p\cdot a_1),(a_1-p\cdot a_1)中的一个$
$\therefore p\cdot a_x\leqslant (p\cdot a_1) , (a_x-p\cdot a_x)\leqslant a_1-p\cdot a_1 $
以此类推
$\therefore q,q2,q3$三个队列都保持单调递减

以下说明来自题解
- 我们会发现蚯蚓的切割具有单调性：一只蚯蚓切割后会分为$⌊px⌋$ 和 $x−⌊px⌋$两个部分，对于其中的任意一个部分，在某一时刻切割出的那只蚯蚓必然会比在它之后切割出来的蚯蚓要长
- 我们用反证法对此予以证明：
- 设某一时刻被选出的某只蚯蚓切割前的长度为 $a_i$，经过 $N$ 秒后，假设存在一只之前未被切割过的蚯蚓这一秒切割完后长度最大，我们记其N秒前的长度为 $a_j$，那么 $a_i$, $a_j$必然要满足（我们先只考虑切割出的$⌊px⌋$ 那部分蚯蚓， $x−⌊px⌋$ 同理）：
$$a_i×p+N×q≤(a_j+N×q)×pa_i×p+N×q≤(a_j+N×q)×p$$
- 分配后得到 $a_i×p+N×q≤a_j×p+N×q×p$
- 又因为 $N$秒前长度为 $a_i$ 的蚯蚓被选出，所以那一时刻满足 $a_i≥a_j$，而 $p$ 的取值范围为$ 0<p<10<p<1$，所以必然满足
$$a_i×p+N×q>a_j×p+N×q×p$$
- 与之前的假设矛盾，因此上述情况不可能存在，我们证得蚯蚓的切割具有单调性
- 考虑记录三个队列，分别存储未切割过的蚯蚓和切割成的两只蚯蚓，每次将蚯蚓插入对应的队尾。
- 根据我们上面推论得出的单调性，每次取出三个队头的最大值即可，蚯蚓长度的增加和上述堆做法的处理方式相同，这样的总复杂为 $O(n+m)$

 #include<algorithm>
 #include<iostream>
 #include<cstdlib>
 #include<cstring>
 #include<cstdio>
 #include<string>
 #include<queue>
 using namespace std;
 #define rint register int
 #define mem(a,b) memset(a,(b),sizeof(a))
 template<typename T>
 inline void read(T &x)
 {
     x=;T w=,ch=getchar();
     while(!isdigit(ch)&&ch!='-')ch=getchar();
     if(ch=='-')w=-,ch=getchar();
     while(isdigit(ch))x=(x<<)+(x<<)+(ch^''),ch=getchar();
     x=x*w;
 }
 typedef long long ll;
 inline bool cmp(ll x,ll y){return x>y;}
 #include<queue>
 queue<ll> q,q1,q2;
 const int maxn=+;
 const ll inf=0x7fffffffffffffff;
 ll n,m,k,t,a[maxn];
 double p;
 inline ll find(){
     ll len=q.empty()?-inf:q.front();
     ll len1=q1.empty()?-inf:q1.front();
     ll len2=q2.empty()?-inf:q2.front();
     if(len>=len1&&len>=len2){q.pop();return len;}
     else if(len1>=len&&len1>=len2){q1.pop();return len1;}
     else{q2.pop();return len2;}
 }
 int main()
 {
     ll U,V;
     read(n);read(m);read(k);read(U);read(V);read(t);p=1.0*U/V;
     for(rint i=;i<=n;i++)read(a[i]);
     sort(a+,a+n+,cmp);
     for(rint i=;i<=n;i++)q.push(a[i]);
     for(rint i=;i<=m;i++){
         ll maxlen=find()+(i-)*k;
     //    cout<<"##"<<maxlen<<endl;
         double d=p*maxlen;
         ll d1,d2;
         d1=d;
         d2=maxlen-d1;
         q1.push(d1-i*k);q2.push(d2-i*k);
         if(!(i%t))printf("%lld ",maxlen);
     }
     putchar('\n');
     for(rint i=;i<=n+m;i++){
         ll maxlen=find();
         if(!(i%t))printf("%lld ",maxlen+m*k);
     }
     return ;
 }