Linux awk工具简单学习记录

awk是一个文本分析工具，它把文件逐行读入，以特定符号将每行切分（默认空格为分隔符），切开的部分再进行各种分析处理。

awk其名称得自于它的创始人Alfred Aho 、Peter Weinberger 和Brian Kernighan 姓氏的首个字母。

事实上，awk有4个不同版本：awk、nawk和gawk，还有一个是mawk。gawk 是AWK的GNU版本，通常未作特别说明的awk一般指的是gawk。在RedHat系统中，默认是gawk，而在Ubuntu系统中，默认是mawk。如果需要使用gawk，可以使用apt-get来进行安装，如下：

sudo apt-get install gawk -y

　　安装完毕后，默认即为gawk，如果还不是默认，可以通过 update-alternatives 命令来进行更改，如下：

sudo update-alternatives --config awk

　　可以通过输入编号来设置默认的awk版本：

下面是关于awk的使用帮助：

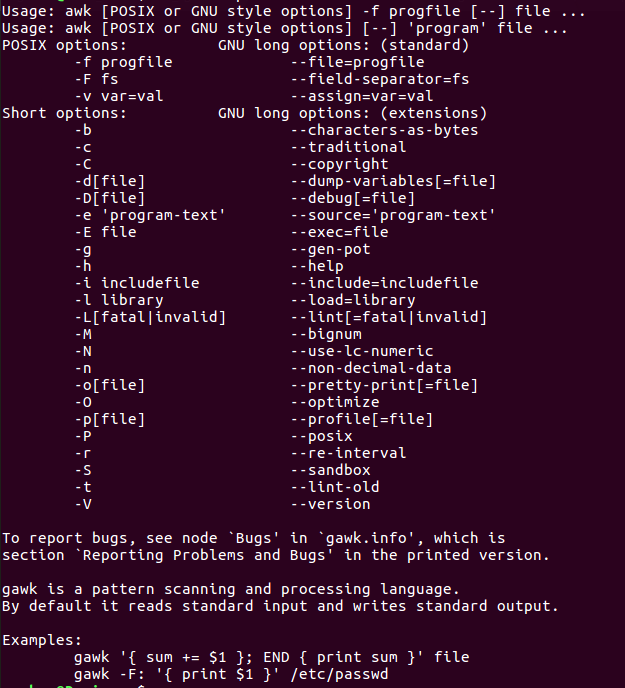
像其他编程语言一样，awk中有一些内置变量，内置变量部分列表如下（重要且常用）：

属性	说明
$0	每次读入的一整行
$1 ~ $n	当前读入行的第n个字段
FS	字段分隔符，默认是空格
NF	当前读入行中的字段个数，也即有多少列
NR	累计读入行的数量，从1开始，多文件处理时累加
FNR	已经读入某一文件行的数量，就是行号，从1开始，多文件处理时不累加
ARGC	命令行参数个数
ARGV	命令行参数数组
BEGIN	程序开始之前要做的事（仅做一次）
END	程序结束之前要做的事（仅做一次）
FILENAME	当前输入文件的名字

awk中的数组无需提前声明，数组下标也不必为整数int类型，可以为字符串string类型，与其说是数组，不如说是映射。

数组下标从1开始，而不是从0开始。

使用for ... in 遍历数组时，每次遍历取得的是数组的index索引，而不是数组元素。

结合上面列举的几个知识点，用个具体例子展示一下。对于有如下的文件：

$ cat word.txt

123456@163.com----a3452801----186035955----123456@163.com
123123@qq.com----wg123123----150731947----123123@qq.com
777888@163.com----li600613----136498718----777888@163.com
456654@qq.com----try649471----134169500----456654@qq.com
159741@qq.com----somechou----186966954----159741@qq.com

　　现在使用awk先输出“第X列”，然后再读取每一列，代码如下：

awk -F'----' 'BEGIN {print "第一列\t\t第二列\t\t第三列\t\t第四列"} {for(a=1;a<=NF;a++) printf("%s\t",$a);print ""}' word.txt

　程序执行结果：

说明：先使用"-F"选项以及"----"字符串指出如何切分每一行，然后在程序开始之前打印一次“第X列”。之后用 for 循环来读取一行中的每一列，for 循环中用到了内置变量NF，NF如前所述，是总的列数量。最后使用 print ""来打印一个换行，print必须带一个空字符串""，否则默认打印每一个列。

下面再用个例子来展示awk中的一种数组功能，文件及其内容依然是上面所给出的那样，这次是将每一列作为一行打印出来，代码如下：

awk -F'----' '{for(a=1;a<=NF;a++) arr[(NR-1)*NF+a]=$a}  END{for(each in arr) print arr[each]}' word.txt

　程序执行结果：

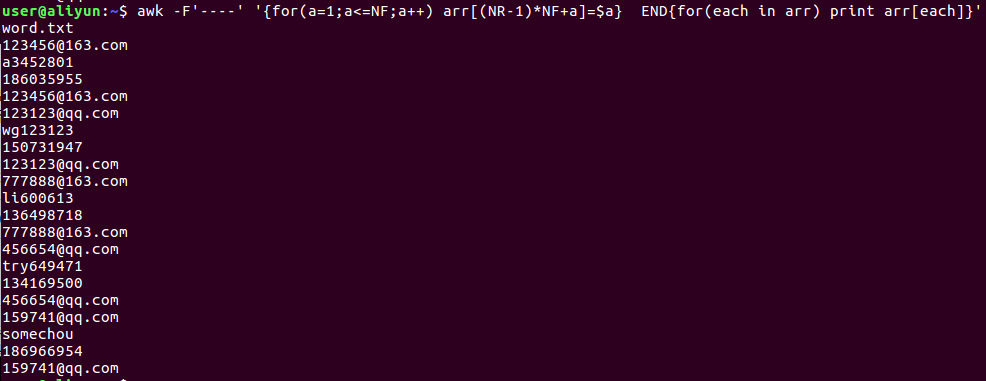
说明：先使用"-F"选项以及"----"字符串指出如何切分每一行。之后用 for 循环来读取一行中的每一列，for 循环中用到了内置变量NF和NR，用NF和NR来计算每一列的index索引并放入数组arr中。这里需要注意的是 a 和 $a，a表示的是下标索引，$a表示的索引对应的值。最后在程序结束之前使用 for ... in 循环遍历数组，将每一列作为一行打印出来。

最后，一个关于awk的坑，在awk中，处理逻辑部分的语句，不要使用双引号，而要使用单引号，否则会出现无法切割的问题，这与shell的变量$是否解释没有关系，如下：

cat a.txt|awk -F "=" "{print 'yes'}"

如果上面的{print yes}使用双引号包含，则会无法切割每一行，必须使用单引号，应该为 ' { print "yes" } '