SSL/TLS All In One

SSL/TLS All In One

HTTPS

SSL/TLS 的工作原理

https://www.websecurity.digicert.com/zh/cn/security-topics/how-ssl-works

浏览器尝试连接受 SSL 保护的网站。

浏览器要求 Web 络服务器确认身份。

服务器向浏览器发送其 SSL 证书副本。

浏览器检查它是否要信任该 SSL 证书。如果信任，则向服务器发送消息。

服务器发回数字签名确认以启动 SSL 加密会话。

SSL / TLS 握手过程

handshake

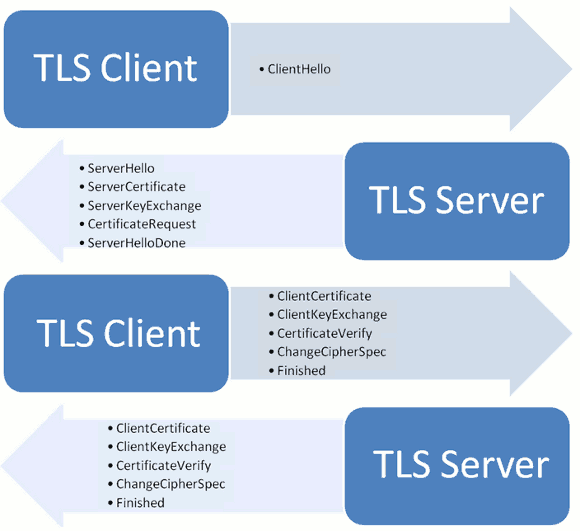
RSA 非对称加密算法

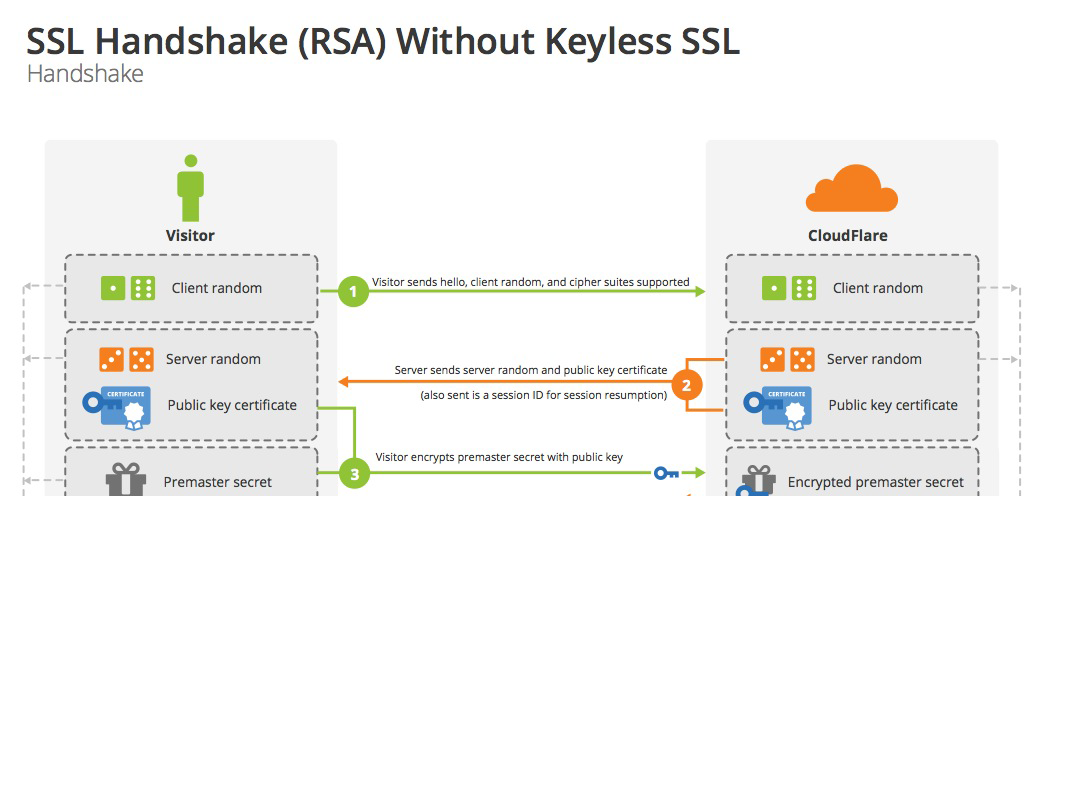
（1）生成对话密钥一共需要三个随机数。

（2）握手之后的对话使用"对话密钥"加密（对称加密），服务器的公钥和私钥只用于加密和解密"对话密钥"（非对称加密），无其他作用。

（3）服务器公钥放在服务器的数字证书之中。

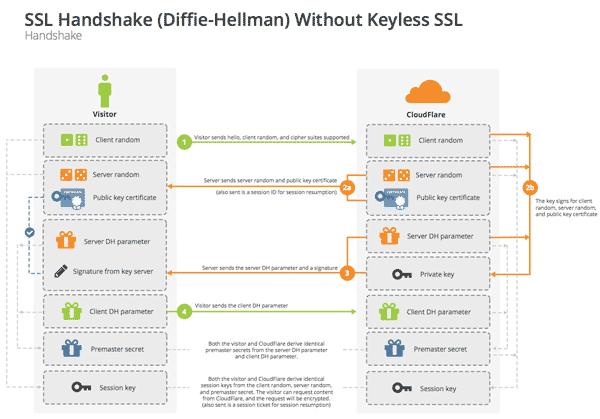
DH 算法

Diffie-Hellman 算法

session的恢复

握手阶段用来建立SSL连接；如果由于某种原因，对话中断，就需要重新握手。

这时有两种方法可以恢复原来的session：一种叫做 session ID，另一种叫做 session ticket。

1. session ID

session ID 的思想很简单，就是每一次对话都有一个编号（session ID）。

如果对话中断，下次重连的时候，只要客户端给出这个编号，且服务器有这个编号的记录，双方就可以重新使用已有的"对话密钥"，而不必重新生成一把。

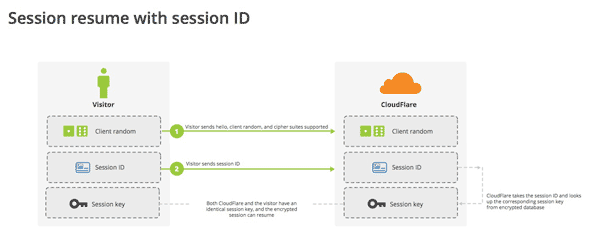
session ID是目前所有浏览器都支持的方法，但是它的缺点在于session ID往往只保留在一台服务器上。

所以，如果客户端的请求发到另一台服务器，就无法恢复对话。

session ticket就是为了解决这个问题而诞生的，目前只有Firefox和Chrome浏览器支持。

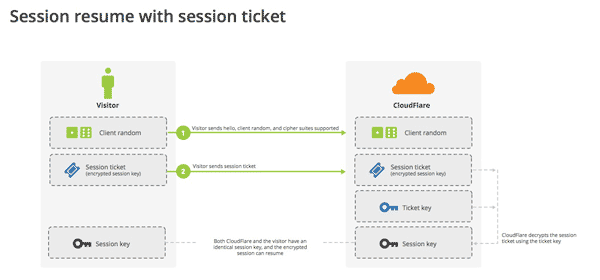
客户端不再发送session ID，而是发送一个服务器在上一次对话中发送过来的session ticket。

这个session ticket是加密的，只有服务器才能解密，其中包括本次对话的主要信息，比如对话密钥和加密方法。当服务器收到session ticket以后，解密后就不必重新生成对话密钥了。

TLS vs SSL

区别 ? rename + upgrade

https://www.ssl2buy.com/wiki/ssl-vs-tls#:~:text=SSL refers to Secure Sockets,same%2C but%2C entirely different.&text=SSL and TLS are cryptographic,%2C systems%2C applications and users.

https://www.globalsign.com/en/blog/ssl-vs-tls-difference

https://www.liquidweb.com/kb/ssl-vs-tls/

结论, SSL和TLS有什么区别？

TLS是SSL的下一个逻辑演进，也是这两种协议中更安全的一种。

除此之外，它们以相同的方式工作，但是较新的版本使用更强的加密类型。

TLS版本1.3是当前最新的首选协议。

https://www.websecurity.digicert.com/security-topics/what-is-ssl-tls-https

https://www.hostingadvice.com/how-to/tls-vs-ssl/

refs

keyless ssl

https://blog.cloudflare.com/announcing-keyless-ssl-all-the-benefits-of-cloudflare-without-having-to-turn-over-your-private-ssl-keys/

http://blog.cloudflare.com/keyless-ssl-the-nitty-gritty-technical-details/

图解 SSL/TLS 协议

http://www.ruanyifeng.com/blog/2014/09/illustration-ssl.html

SSL/TLS 协议运行机制的概述

http://www.ruanyifeng.com/blog/2014/02/ssl_tls.html

---

---

xgqfrms 2012-2020

www.cnblogs.com 发布文章使用：只允许注册用户才可以访问！

---