自已动手作图搞清楚AVL树
@
一、背景
二叉树是一种常用的数据结构,更是实现众多算法的一把利器。(可参考《自己动手作图深入理解二叉树、满二叉树及完全二叉树》)
二分搜索树(Binary Search Tree)做为一种能实现快速定位查找的二叉树也得到了广泛应用(底层实现可参考《用一个图书库实例搞懂二分搜索树的底层原理》)。
1 二分搜索树是一颗二叉树
2 二分搜索树每个节点的左子树的值都小于该节点的值,每个节点右子树的值都大于该节点的值
3 任意一个节点的每棵子树都满足二分搜索树的定义
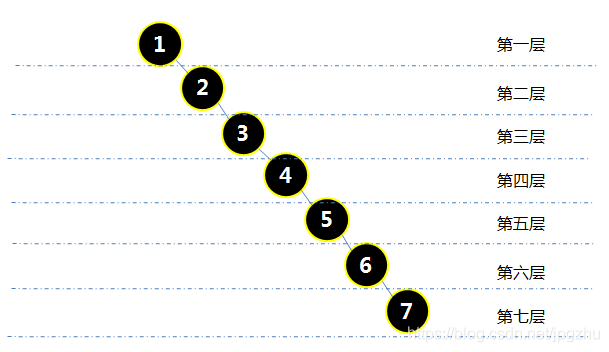
- 但二分搜索树也有其局限性:比如我们给定[1,2,3,4,5,6,7]这样的数据并按顺序构成的二分搜索树就褪化成了线性链表,二分搜索树极度偏向右侧,且深度达到7级,查找搜索的时间复杂度也从O(logn)褪化成了O(n).
二、平衡二分搜索树---AVL树
- 为了解决二分搜索树的不平衡性,科学家创造一种自平衡的二分搜索树,这种树也被简称为AVL(G. M. Adelson-Velsky和E. M. Landis)树,以下的图即为一棵AVL树:
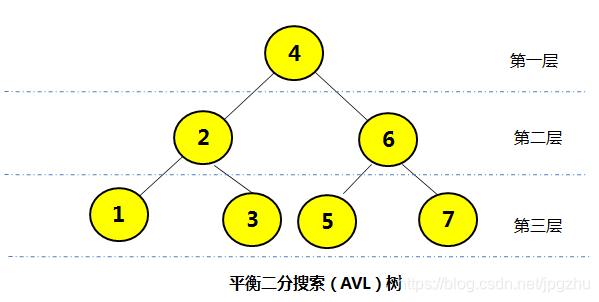
2.1 AVL树的基本概念
每个结点的左右子树的高度之差(平衡因子)不大于1的二分搜索树,即为AVL树。
结点
- 结点是组成二叉树的最小单元。
-- 用图形表示

-- 用代码表示
// 结点
class Node<E> {
E e;
Node left, right;
Node(E e) {
this.e= e;
this.left = null;
this.right = null;
}
}
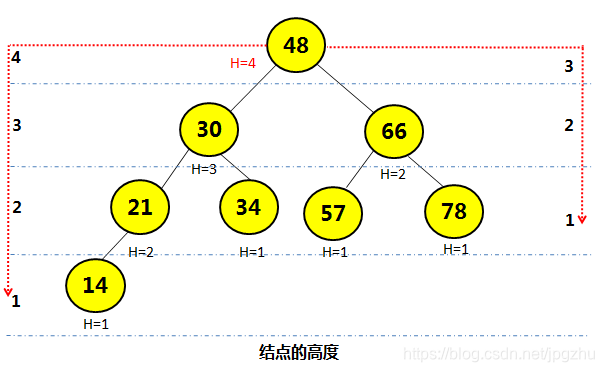
高度
- 叶子结点高度默认为1;非叶子结点的高度为该结点能到达的左子树或右子树的叶子结点的最大跨度。
-- 用代码描述
class Node<E> {
E e;
Node left, right;
// 高度
int height;
Node(E e) {
this.e = e;
this.left = null;
this.right = null;
// 叶子结点高度默认为1
this.height = 1;
}
}
// 获得节点node的高度
private int getHeight(Node node) {
if (node == null) {
return 0;
}
return node.height;
}
// 计算结点的高度
private void setHeight(Node node) {
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
}
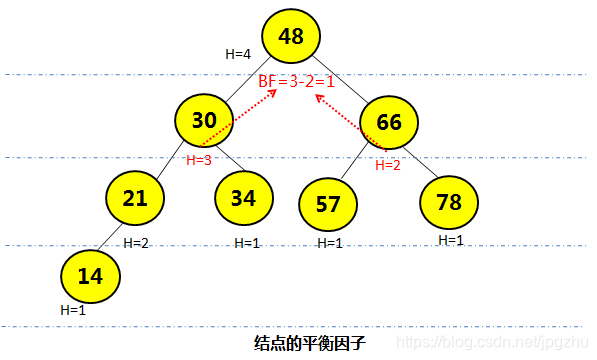
平衡因子
- 叶子结点的平衡因子为0;非叶子结点的平衡因子为该结点的左子结点或右子结点的高度差。
-- 用代码描述
class Node<E> {
E e;
Node left, right;
// 高度
int height;
Node(E e) {
this.e = e;
this.left = null;
this.right = null;
// 叶子结点高度默认为1
this.height = 1;
}
}
// 获得节点node的高度
private int getHeight(Node node) {
if (node == null) {
return 0;
}
return node.height;
}
// 获得节点node的平衡因子
private int getBalanceFactor(Node node){
if(node == null)
return 0;
return getHeight(node.left) - getHeight(node.right);
}
2.2 AVL树的验证
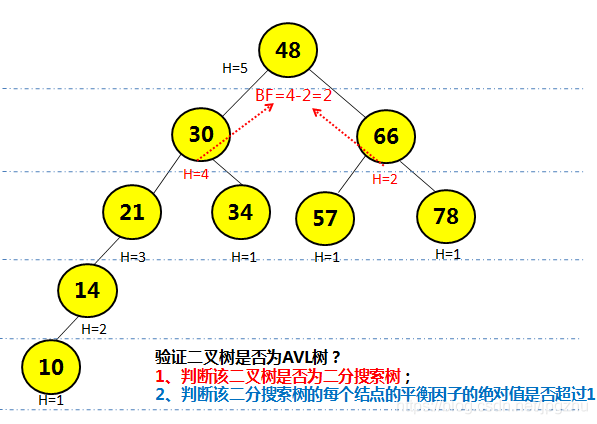
- 按AVL的定义,判断一棵二叉树是否为AVL树
- 首先需判断这棵二叉树是否为二分搜索树:即从根结点开始中序遍历该二叉树,形成的遍历序列一定是按从小到大有序排列的。
- 其实判断该二分搜索树的每个结点的平衡因子的绝对值是否超过1。
-- 用代码描述
/**
* AVL树
* @param <E> 泛型元素
* @author zhuhuix
* @date 2020-07-21
*/
public class AVL<E extends Comparable<E>> {
// 私有内部类-树结点
private class Node<E> {
E e;
Node left, right;
// 高度
int height;
Node(E e) {
this.e = e;
this.left = null;
this.right = null;
this.height = 1;
}
}
// 根结点
private Node root;
// 获得节点node的高度
private int getHeight(Node node) {
if (node == null) {
return 0;
}
return node.height;
}
// 计算结点的高度
private int setHeight(Node node) {
return node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
}
// 获得节点node的平衡因子
private int getBalanceFactor(Node node) {
if (node == null) {
return 0;
}
return getHeight(node.left) - getHeight(node.right);
}
// 增加元素
public void add(E e) {
root = addNode(root, e);
}
// 通过递归算法遍历现有结点,将新结点插入到合适的位置
private Node addNode(Node node, E element) {
if (node == null) {
System.out.println("新增元素[" + element + "] height=1");
return new Node(element);
}
// 新加入元素小于结点值,往左子树增加
if (element.compareTo((E) node.e) < 0) {
node.left = addNode(node.left, element);
// 新加入元素大于结点值,往右子树增加
} else if (element.compareTo((E) node.e) > 0) {
node.right = addNode(node.right, element);
} else // element.compareTo(node.e) == 0
{
node.e = element;
}
// 更新height
node.height = setHeight(node);
System.out.println("元素[" + node.e + "] 更新高度: height=" + node.height);
return node;
}
// 判断二叉树是否为二分搜索树:从根结点中序遍历形成的序列是否从小到大有序排列
public boolean isBST() {
ArrayList<E> arrayList = new ArrayList<>();
InOrderTraversal(root, arrayList);
for (int i = 0; i < arrayList.size() - 1; i++) {
// 相邻两个元素比较,如果前一个元素大于后一个元素,则不为二分搜索树
if (arrayList.get(i).compareTo(arrayList.get(i + 1)) > 0) {
return false;
}
}
System.out.println("中序遍历:" + arrayList.toString());
return true;
}
// 通过中序遍历形成序列
private void InOrderTraversal(Node node, ArrayList<E> arrayList) {
if (node == null) {
return;
}
InOrderTraversal(node.left, arrayList);
arrayList.add((E) node.e);
InOrderTraversal(node.right, arrayList);
}
// 判断是否是一棵平衡二叉树
public boolean isBalancedTree() {
return isBalanced(root);
}
// 通过递归遍历判断是否为平衡二叉树:判断每个结点的平衡因子的绝对值是否有大于1的存在
private boolean isBalanced(Node node) {
if (node == null) {
return true;
}
// 获取该结点的平衡因子,并判断平衡因子的绝对值是否大于1
int balanceFactor = getBalanceFactor(node);
if (Math.abs(balanceFactor) > 1) {
System.out.println("元素["+node.e + "] 平衡因子=" + balanceFactor+",超过1");
System.out.println("元素["+node.e+ "] 左子树的高度="+node.left.height+ ",右子树的高度="+node.right.height);
return false;
}
// 遍历判断结点的左子树和右子树的各个结点
return isBalanced(node.left) && isBalanced(node.right);
}
public static void main(String[] args) {
// 定义一个数组
Integer[] arr = {48, 30, 66, 21, 34, 57, 78, 14};
// 将该数组构建成一个二分搜索树
AVL<Integer> avl = new AVL<>();
for (int i = 0; i < arr.length; i++) {
avl.add(arr[i]);
}
// 判断当前的二叉树是否满足二分搜索树的定义
boolean isBST = avl.isBST();
boolean isBalance = avl.isBalancedTree();
// 判断当前的树是否满足AVL定义
if (isBST && isBalance) {
System.out.println("该二叉树满足二分搜索树及平衡的条件,是AVL树!!!");
} else {
System.out.println("该二叉树不是AVL树;" + "是否满足二分搜索树条件:" + isBST + " ;是否满足平衡条件:" + isBalance);
}
// 给该AVL树加上一个结点,再次判断是否判断
avl.add(10);
// 判断当前的二叉树是否满足二分搜索树的定义
isBST = avl.isBST();
isBalance = avl.isBalancedTree();
// 判断当前的树是否满足AVL定义
if (isBST && isBalance) {
System.out.println("该二叉树满足二分搜索树及平衡的条件,是AVL树!!!");
} else {
System.out.println("该二叉树不是AVL树;" + "是否满足二分搜索树条件:" + isBST + " ;是否满足平衡条件:" + isBalance);
}
}
}
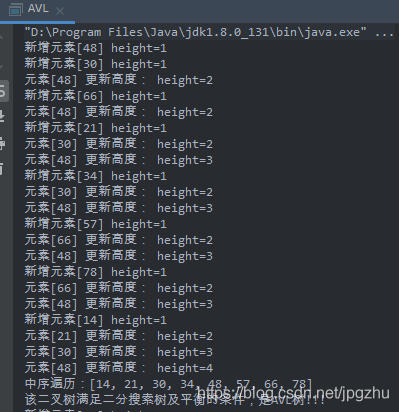
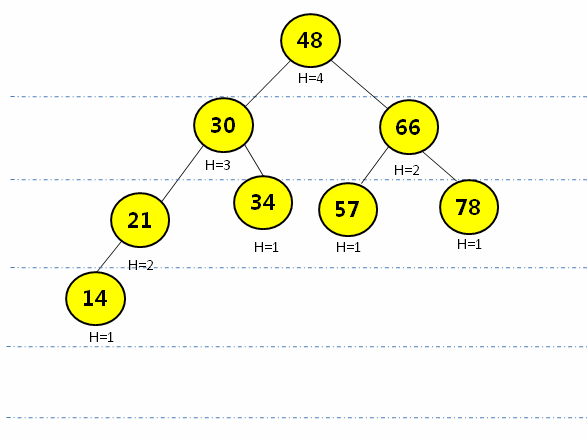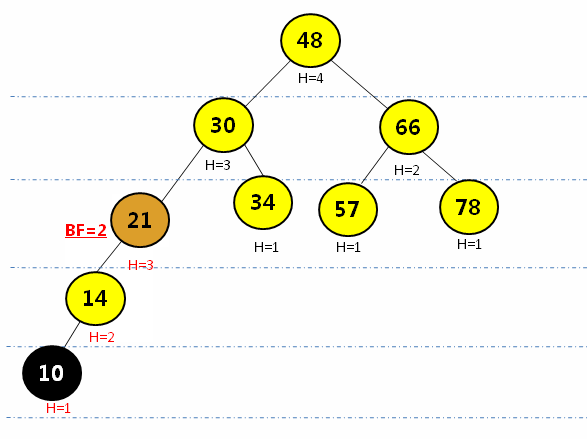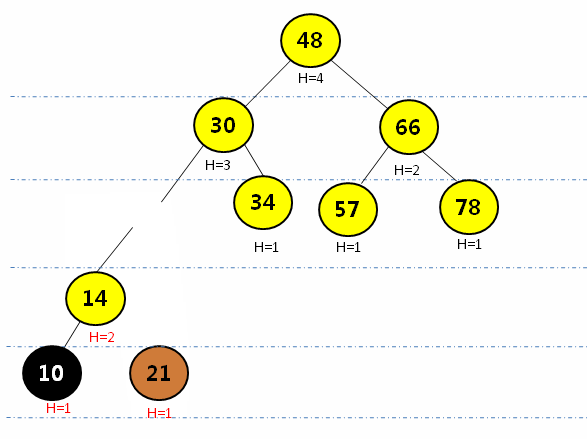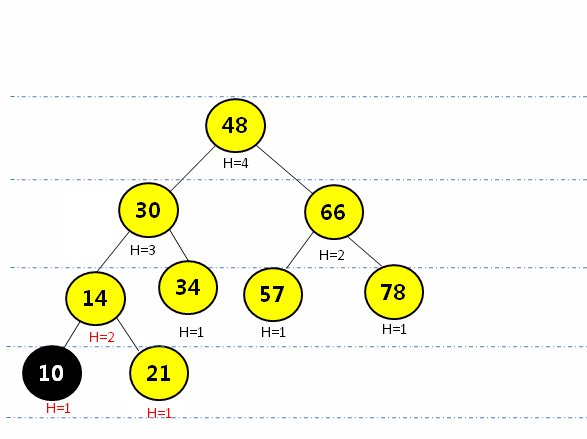
通过{48, 30, 66, 21, 34, 57, 78, 14}构建AVL树
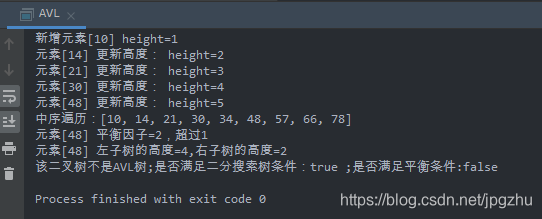
给以上AVL树增加一个结点10,再次判断该树是否满足AVL的定义
三、旋转操作
往AVL树中添加结点很可能会导致失去平衡,所以我们需要在每次插入结点后进行平衡的维护。破坏平衡性有如下四种情况:
3.1 L L--需要通过右旋操作
- 在结点的左子树(L)的左孩子(L)添加新的结点,会导致失去平衡:
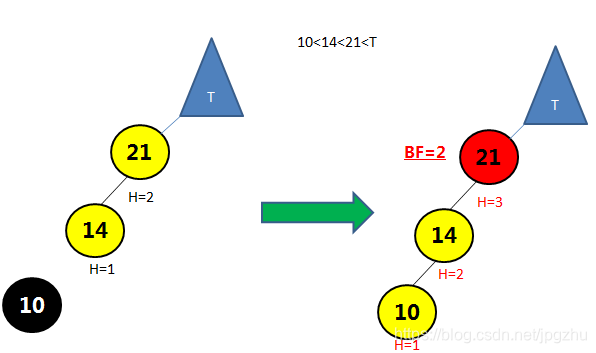
- 通过右旋操作(顺时针转)将平衡因子大于1的结点进行调整
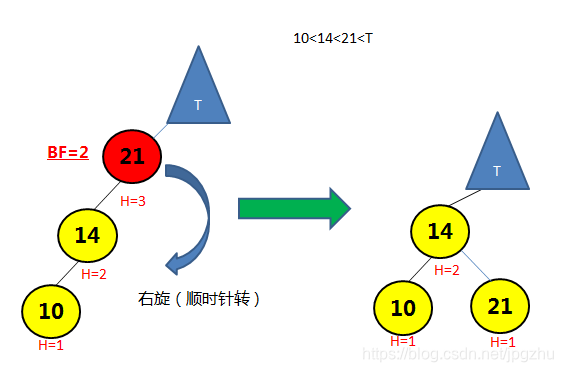
- 完整动画演示
- 代码处理
// 右旋(顺时针转)
private Node rightRotate(Node y) {
Node x = y.left;
Node T = x.right;
// 向右旋转过程
x.right = y;
y.left = T;
// 更新height
y.height = setHeight(y);
System.out.println("元素[" + y.e + "] 右旋后更新高度: height=" + y.height);
x.height = setHeight(x);
System.out.println("元素[" + x.e + "] 更新高度: height=" + x.height);
return x;
}
3.2 R R--需要通过左旋操作
- 在结点的右子树(R)的右孩子(R)添加新的结点,会导致失去平衡:
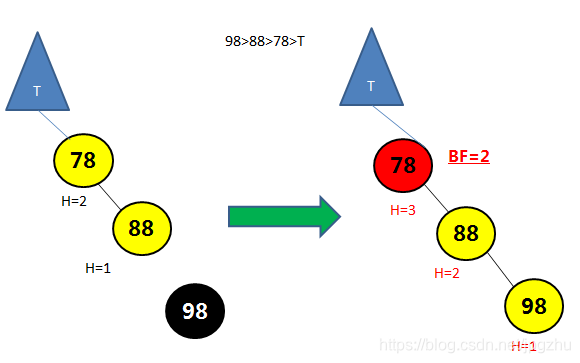
- 通过左旋操作(逆时针转)将平衡因子大于1的结点进行调整
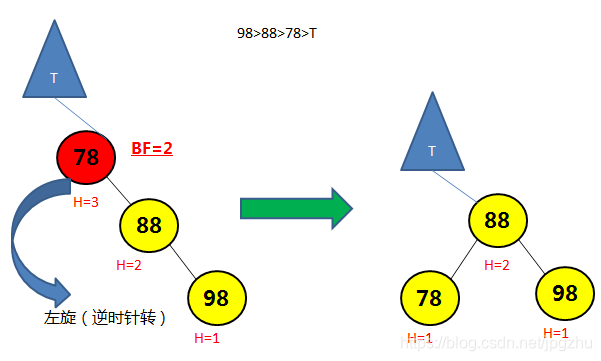
- 完整动画演示

- 代码处理
// 左旋(逆时针转)
private Node leftRotate(Node y) {
Node x = y.right;
Node T = x.left;
// 向左旋转过程
x.left = y;
y.right = T;
// 更新height
y.height = setHeight(y);
System.out.println("元素[" + y.e + "] 左旋后更新高度: height=" + y.height);
x.height = setHeight(x);
System.out.println("元素[" + x.e + "] 更新高度: height=" + x.height);
return x;
}
3.3 L R--需要先通过左旋再右旋操作
- 在结点的左子树(L)的右孩子(R)添加新的结点,会导致失去平衡:
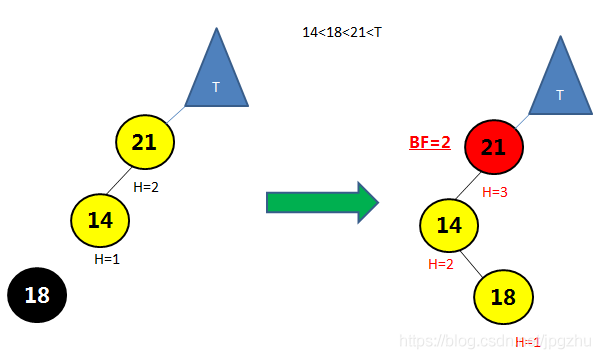
- 先通过左子结点的左旋操作(逆时针转)转成LL形式,再通过右旋操作(顺时针转)将平衡因子大于1的结点进行调整
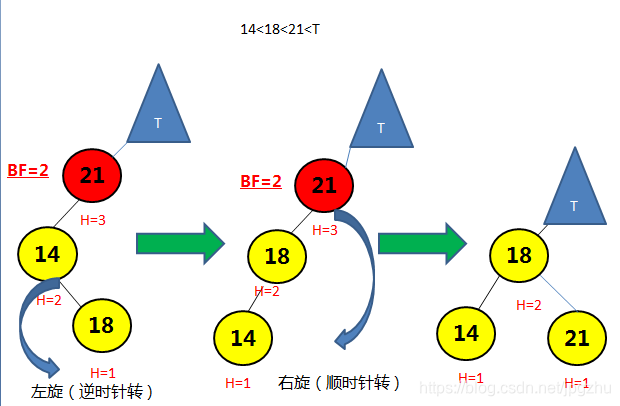
- 完整动画演示
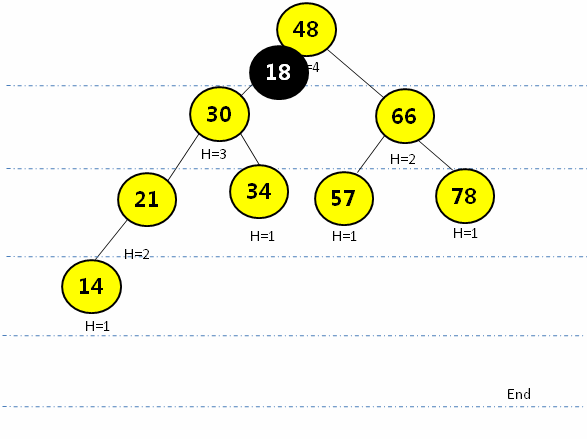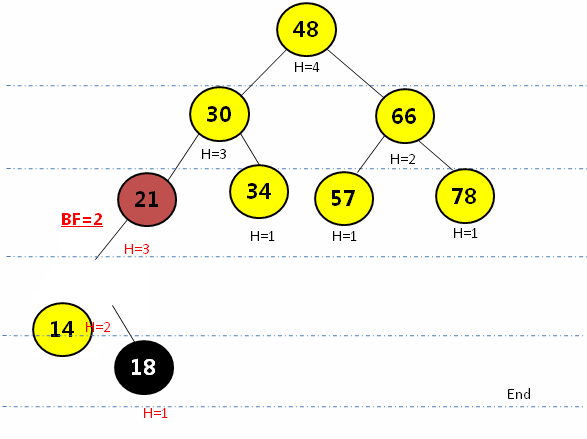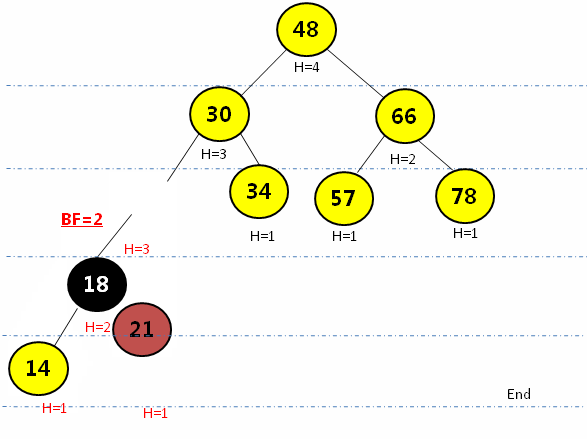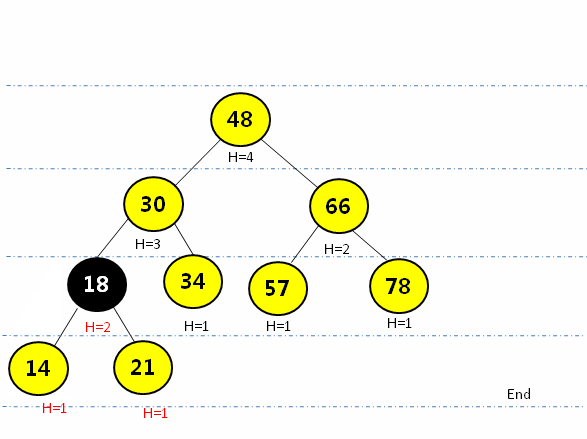
2.4 R L--需要先通过右旋再左旋操作
- 在结点的右子树(R)的左孩子(L)添加新的结点,会导致失去平衡:
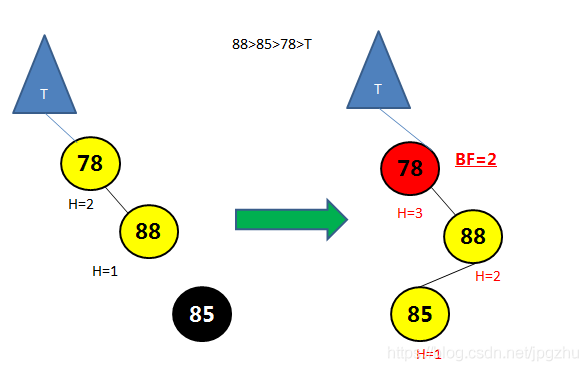
- 先通过右子结点的右旋操作(顺时针转)转成RR形式,再通过左旋操作(逆时针转)将平衡因子大于1的结点进行调整
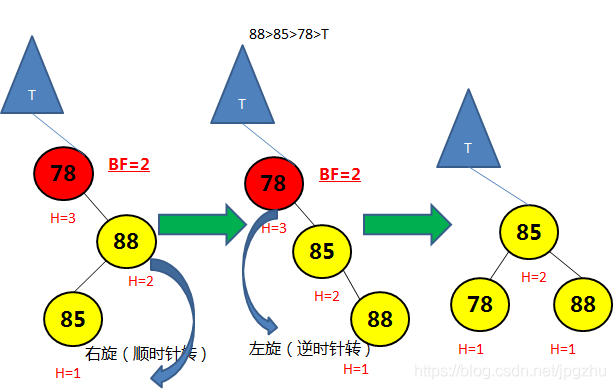
- 完整动画演示
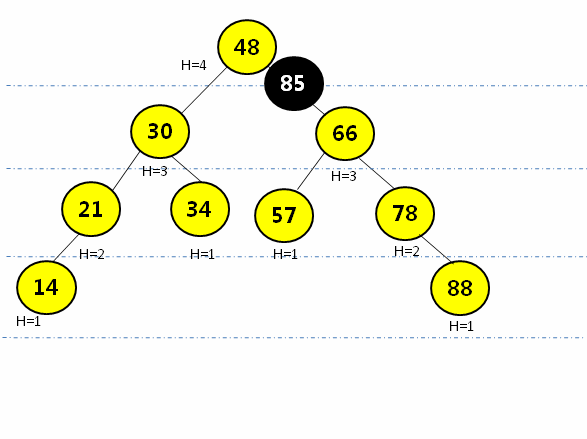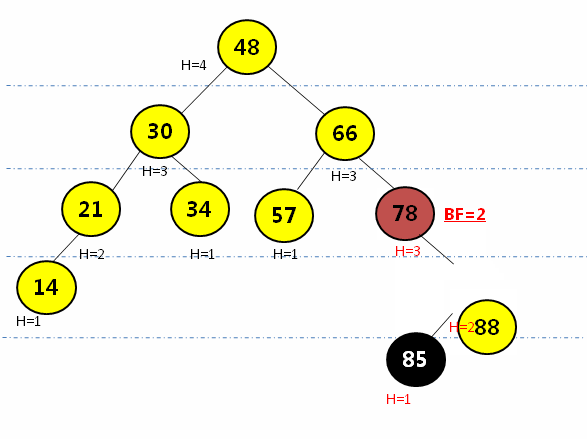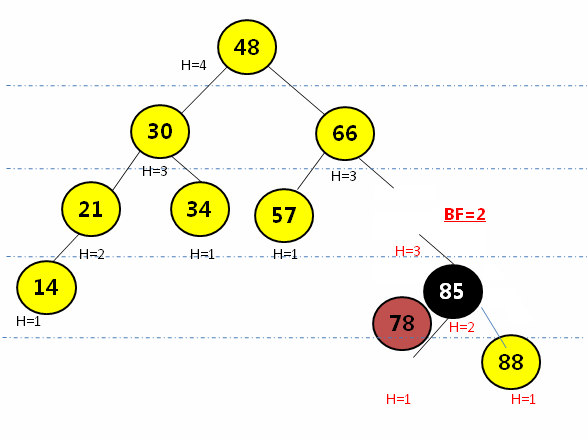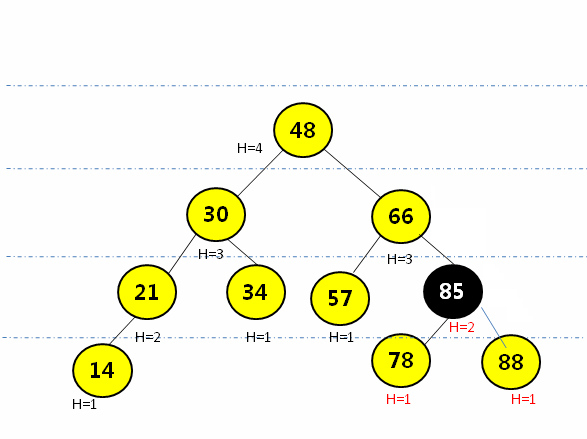
四、AVL树完整代码实现
/**
* AVL树
*
* @param <E> 元素
* @author zhuhuix
* @date 2020-07-21
*/
public class AVL<E extends Comparable<E>> {
// 私有内部类-树结点
private class Node<E> {
E e;
Node left, right;
// 高度
int height;
Node(E e) {
this.e = e;
this.left = null;
this.right = null;
this.height = 1;
}
}
// 根结点
private Node root;
// 获得节点node的高度
private int getHeight(Node node) {
if (node == null) {
return 0;
}
return node.height;
}
// 计算结点的高度
private int setHeight(Node node) {
return node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
}
// 获得节点node的平衡因子
private int getBalanceFactor(Node node) {
if (node == null) {
return 0;
}
return getHeight(node.left) - getHeight(node.right);
}
// 右旋(顺时针转)
private Node rightRotate(Node y) {
Node x = y.left;
Node T = x.right;
// 向右旋转过程
x.right = y;
y.left = T;
// 更新height
y.height = setHeight(y);
System.out.println("元素[" + y.e + "] 右旋后更新高度: height=" + y.height);
x.height = setHeight(x);
System.out.println("元素[" + x.e + "] 更新高度: height=" + x.height);
return x;
}
// 左旋(逆时针转)
private Node leftRotate(Node y) {
Node x = y.right;
Node T = x.left;
// 向左旋转过程
x.left = y;
y.right = T;
// 更新height
y.height = setHeight(y);
System.out.println("元素[" + y.e + "] 左旋后更新高度: height=" + y.height);
x.height = setHeight(x);
System.out.println("元素[" + x.e + "] 更新高度: height=" + x.height);
return x;
}
// 增加元素
public void add(E e) {
root = addNode(root, e);
}
// 通过递归算法遍历现有结点,将新结点插入到合适的位置
private Node addNode(Node node, E element) {
if (node == null) {
System.out.println("新增元素[" + element + "] height=1");
return new Node(element);
}
// 新加入元素小于结点值,往左子树增加
if (element.compareTo((E) node.e) < 0) {
node.left = addNode(node.left, element);
// 新加入元素大于结点值,往右子树增加
} else if (element.compareTo((E) node.e) > 0) {
node.right = addNode(node.right, element);
} else // element.compareTo(node.e) == 0
{
node.e = element;
}
// 更新height
node.height = setHeight(node);
System.out.println("元素[" + node.e + "] 更新高度: height=" + node.height);
// 计算平衡因子
int balanceFactor = getBalanceFactor(node);
if (node != null) {
System.out.println("元素[" + node.e + "] "
+ "左子结点为:[" + (node.left == null ? "" : node.left.e) + "]"
+ "右子结点为:[" + (node.right == null ? "" : node.right.e) + "]"
+ ",balanceFactor=" + balanceFactor);
}
// 平衡维护
if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
System.out.println("元素[" + node.e + "] balanceFactor=" + balanceFactor + ",进行右旋");
return rightRotate(node);
}
if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0) {
System.out.println("元素[" + node.e + "] balanceFactor=" + balanceFactor + ",进行左旋");
return leftRotate(node);
}
if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
System.out.print("元素[" + node.e + "] balanceFactor=" + balanceFactor + " 先将[" + node.e + "的左子结点" + node.left.e + "] 进行左旋");
node.left = leftRotate(node.left);
System.out.println("再将元素[" + node.e + "] 进行右旋");
return rightRotate(node);
}
if (balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
System.out.print("元素[" + node.e + "] balanceFactor=" + balanceFactor + " 先将[" + node.e + "的右子结点" + node.right.e + "] 进行右旋");
node.right = rightRotate(node.right);
System.out.println("再将元素[" + node.e + "] 进行左旋");
return leftRotate(node);
}
return node;
}
// 判断二叉树是否为二分搜索树:从根结点中序遍历形成的序列是否从小到大有序排列
public boolean isBST() {
ArrayList<E> arrayList = new ArrayList<>();
InOrderTraversal(root, arrayList);
for (int i = 0; i < arrayList.size() - 1; i++) {
// 相邻两个元素比较,如果前一个元素大于后一个元素,则不为二分搜索树
if (arrayList.get(i).compareTo(arrayList.get(i + 1)) > 0) {
return false;
}
}
System.out.println("中序遍历:" + arrayList.toString());
return true;
}
// 通过中序遍历形成序列
private void InOrderTraversal(Node node, ArrayList<E> arrayList) {
if (node == null) {
return;
}
InOrderTraversal(node.left, arrayList);
arrayList.add((E) node.e);
InOrderTraversal(node.right, arrayList);
}
// 前序遍历打印
public void preOrderTraversal() {
ArrayList<E> arrayList = new ArrayList<>();
preOrderTraversal(root, arrayList);
System.out.println("前序遍历" + arrayList);
}
// 通过前序遍历形成序列
private void preOrderTraversal(Node node, ArrayList<E> arrayList) {
if (node == null) {
return;
}
arrayList.add((E) node.e);
preOrderTraversal(node.left, arrayList);
preOrderTraversal(node.right, arrayList);
}
// 判断是否是一棵平衡二叉树
public boolean isBalancedTree() {
return isBalanced(root);
}
// 通过递归遍历判断是否为平衡二叉树:判断每个结点的平衡因子的绝对值是否有大于1的存在
private boolean isBalanced(Node node) {
if (node == null) {
return true;
}
// 获取该结点的平衡因子,并判断平衡因子的绝对值是否大于1
int balanceFactor = getBalanceFactor(node);
if (Math.abs(balanceFactor) > 1) {
System.out.println("元素[" + node.e + "] 平衡因子=" + balanceFactor + ",超过1");
System.out.println("元素[" + node.e + "] 左子树的高度=" + node.left.height + ",右子树的高度=" + node.right.height);
return false;
}
// 遍历判断结点的左子树和右子树的各个结点
return isBalanced(node.left) && isBalanced(node.right);
}
public static void main(String[] args) {
// 定义一个数组
Integer[] arr = {48, 30, 66, 21, 34, 57, 78, 14};
// 将该数组构建成一个二分搜索树
AVL<Integer> avl = new AVL<>();
for (int i = 0; i < arr.length; i++) {
avl.add(arr[i]);
}
// 判断当前的二叉树是否满足二分搜索树的定义
boolean isBST = avl.isBST();
boolean isBalance = avl.isBalancedTree();
// 判断当前的树是否满足AVL定义
if (isBST && isBalance) {
System.out.println("该二叉树满足二分搜索树及平衡的条件,是AVL树!!!");
} else {
System.out.println("该二叉树不是AVL树;" + "是否满足二分搜索树条件:" + isBST + " ;是否满足平衡条件:" + isBalance);
}
// 给该AVL树加上一个结点,再次判断是否判断
avl.add(10);
// 判断当前的二叉树是否满足二分搜索树的定义
isBST = avl.isBST();
isBalance = avl.isBalancedTree();
// 判断当前的树是否满足AVL定义
if (isBST && isBalance) {
System.out.println("该二叉树满足二分搜索树及平衡的条件,是AVL树!!!");
} else {
System.out.println("该二叉树不是AVL树;" + "是否满足二分搜索树条件:" + isBST + " ;是否满足平衡条件:" + isBalance);
}
}
}
- 构建AVL树过程
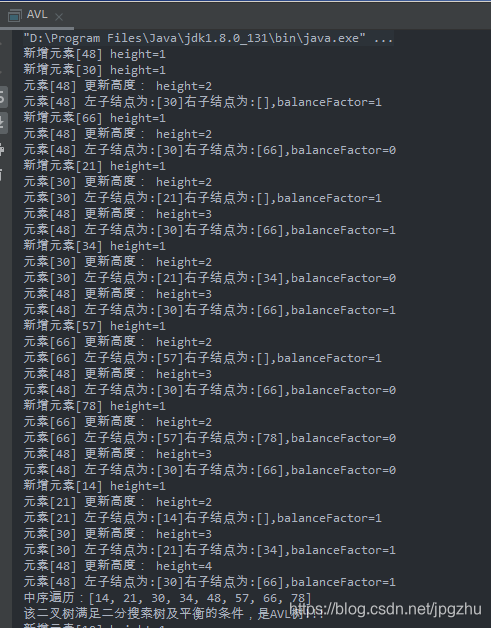
- 添加结点AVL树平衡过程

自已动手作图搞清楚AVL树的更多相关文章
- 自己动手实现java数据结构(七) AVL树
1.AVL树介绍 前面我们已经介绍了二叉搜索树.普通的二叉搜索树在插入.删除数据时可能使得全树的数据分布不平衡,退化,导致二叉搜索树最关键的查询效率急剧降低.这也引出了平衡二叉搜索树的概念,平衡二叉搜 ...
- AVL树与红黑树
平衡树是平时经常使用数据结构. C++/JAVA中的set与map都是通过红黑树实现的. 通过了解平衡树的实现原理,可以更清楚的理解map和set的使用场景. 下面介绍AVL树和红黑树. 1. AVL ...
- AVL 树的插入、删除、旋转归纳
参考链接: http://blog.csdn.net/gabriel1026/article/details/6311339 1126号注:先前有一个概念搞混了: 节点的深度 Depth 是指从根 ...
- 数据结构与算法(九):AVL树详细讲解
数据结构与算法(一):基础简介 数据结构与算法(二):基于数组的实现ArrayList源码彻底分析 数据结构与算法(三):基于链表的实现LinkedList源码彻底分析 数据结构与算法(四):基于哈希 ...
- java项目---用java实现二叉平衡树(AVL树)并打印结果(详)(3星)
package Demo; public class AVLtree { private Node root; //首先定义根节点 private static class Node{ //定义Nod ...
- 线程安全使用(四) [.NET] 简单接入微信公众号开发:实现自动回复 [C#]C#中字符串的操作 自行实现比dotcore/dotnet更方便更高性能的对象二进制序列化 自已动手做高性能消息队列 自行实现高性能MVC WebAPI 面试题随笔 字符串反转
线程安全使用(四) 这是时隔多年第四篇,主要是因为身在东软受内网限制,好多文章就只好发到东软内部网站,懒的发到外面,现在一点点把在东软写的文章给转移出来. 这里主要讲解下CancellationT ...
- AVL树(查找、插入、删除)——C语言
AVL树 平衡二叉查找树(Self-balancing binary search tree)又被称为AVL树(AVL树是根据它的发明者G. M. Adelson-Velskii和E. M. Land ...
- AVL树(二叉平衡树)详解与实现
AVL树概念 前面学习二叉查找树和二叉树的各种遍历,但是其查找效率不稳定(斜树),而二叉平衡树的用途更多.查找相比稳定很多.(欢迎关注数据结构专栏) AVL树是带有平衡条件的二叉查找树.这个平衡条件必 ...
- 数据结构与算法-基础(十一)AVL 树
AVL 树 是最早时期发明的自平衡二叉搜索树之一.是依据它的两位发明者的名称命名. AVL 树有一个重要的属性,即平衡因子(Balance Factor),平衡因子 == 某个节点的左右子树高度差. ...
随机推荐
- Spring Boot]SpringBoot四大神器之Actuator
论文转载自博客: https://blog.csdn.net/Dreamhai/article/details/81077903 https://bigjar.github.io/2018/08/19 ...
- linux网络编程-posix信号量与互斥锁(39)
-posix信号量信号量 是打开一个有名的信号量 sem_init是打开一个无名的信号量,无名信号量的销毁用sem_destroy sem_wait和sem_post是对信号量进行pv操作,既可以使用 ...
- mysql replace替换某字段的值
由于最近我们的一个网站回购了一个很好的域名所有与之相关的项目都需要修改: 今天接到一个任务将我们会员开通的个人网站的二级域名换成新域名,看了一下库已开通的还很少才2w多,且要换的和之前库中的数据很规则 ...
- Win8.1卸载64位Oracle Database 11g的详细图文步骤记录
Oracle Database 11g在Win8 上的卸载过程记录. Step1停用oracle服务:进入计算机管理/任务管理器,在服务中,找到oracle开头的所有服务,右击选择停止: Step2 ...
- SpringSceurity(5)---短信验证码登陆功能
SpringSceurity(5)---短信验证码登陆功能 有关SpringSceurity系列之前有写文章 1.SpringSecurity(1)---认证+授权代码实现 2.SpringSecur ...
- 双缓冲显示字幕(卡拉ok字幕)
思路: 1.设置定时器SetTime,在Ontime()里面确定显示矩形的大小,让后用DrawText把字铁道矩形上面: 2. int nTextHei = dc.GetTextExtent( m_s ...
- paramiko报错 Garbage packet received
前情概要 今天想要写一个多进程的python脚本上传代码至服务器,于是在本地用虚拟机测试了一下,可总是报错,具体报错信息如下 Traceback (most recent call last): Fi ...
- 想做时间管理大师?你可以试试Mybatis Plus代码生成器
1. 前言 对于写Crud的老司机来说时间非常宝贵,一些样板代码写不但费时费力,而且枯燥无味.经常有小伙伴问我,胖哥你怎么天天那么有时间去搞新东西,透露一下秘诀呗. 好吧,今天就把Mybatis-pl ...
- C++ MFC 文件操作(新建,删除,剪切,复制,读数据,写数据,重命名)
源文件:http://pan.baidu.com/s/1ve0hV 这是运行mfc缺失的dll动态链接库:http://pan.baidu.com/s/17pGlT 哈哈,我也是初接触C++,基础的什 ...
- C# wpf 实现 MD5加密解密 小工具
源文件: http://pan.baidu.com/share/link?shareid=2038099474&uk=3912660076 MD5 C# 实现代码来源于网络,感谢原系作者! 参 ...

