字节真题 ZJ26-异或：使用字典树减少计算次数

原题链接

题目描述：

个人分析：从输入数据看，要处理的元素个数（n）没有到达 10^9 或 10^8 级，或许可以使用暴力？但是稍微计算一下，有 10^5 * (10^5 - 1) / 2 = 10^10 / 2

个结果，说明至少运算那么多次。假设每次运算使用1ns(CPU运算速度纳秒为单位)，貌似没有超时，但是加上内存分配，数组越界检查等时间，大概率超时。

需要有一种办法减少重复运算，首先需要了解异或运算的特性：（以下讨论均是正数情况，因为题目的输入范围均是正数）

a 和 b 从高位开始逐位异或，只有两者相应位上的数不同，结果才能是1。

a 和 b 某一位上 异或的结果如果是1 ，并且待比较数上相应位的数是0，说明 a 和 b 异或的结果必定大于待比较数

因为异或结果在高位上大于待比较数，低位就不需要比较了。也就是说，a 和 任何 前缀与 b 相同的数异或，结果都会大于待比较数，因为异或出来的结果

必然和 c 有共同的前缀，有这样的前缀的话，就比如比待比较数大

     

于是得到思路：

如果找到一种能对相同前缀元素进行计数的数据结构，就可以直接返回符合前缀条件的元素个数，减少运算。

字典树：Trie Tree 正好是满足预期的数据结构

我的思路 ：

题目要输入 n 个数，求出 这 n 个数两两异或后 大于 m 的结果。

或许可以先向字典树中插入一个数 A1 ，先保证数不空，而且题目中保证了输入的数的数量大于1个，所以必能有第一个数 A1 插入字典树

对于之后输入的数 Ax (x > 1)，先去字典树里找有几个和 Ax 异或后结果大于 m 的数 （寻找过程见后文），然后再把 Ax 插入到字典树中。

不怕 Ax 错过 之后的 Ax+1 , Ax+2, ......，因为Ax+1, Ax+2,...... 会遇到前面已经在字典树里的Ax，异或运算可交换，a^b = b^a

伪代码: 含义是先把A1插入字典树，之后输入的Ax，都要先去树里找和 他异或大于m 的数有多少个，并且把数量进行累积

tree.insert(A1);

int total = 0;

for( input Ax ){

　　total += tree.compare(Ax, m);

　　 tree.insert(Ax);

}

output total

 实操：（JDK 1.8）

1.打好框架：

　　输入输出流

　　字典树申明

import java.util.Scanner;
 
public class Xor {
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        TrieTree tree = new TrieTree();
 
        while(sc.hasNext()){
            int n = sc.nextInt();
            int m = sc.nextInt();
            long total = 0;
　　　　　　　 //插入A1
            tree.insert(sc.nextInt());
            for(int i = 0; i < n - 1; i ++){
                int me = sc.nextInt();
             　 //找出和Ax异或后结果大于m的数有多少个，并且累加
　　　　　　　    total += tree.compare(me, m);
　　　　　　　　  //插入Ax
                tree.insert(me);
            }
　　　　　　　//输出结果
            System.out.println(total);
        }
    }
    private static class Node{
　　　　 //有多少个数有当前前缀
        public int count = 1;
　　　　 //子节点
        public Node[] child = new Node[2];
    }
 
    private static class TrieTree{
　　　　 //根节点
        Node root;
　　　　
        public TrieTree(){
            //根节点不包含信息，卫星数据
　　　　　　  this.root = new Node();
        }
 
        public int compare(int tar, int m){
        }
 
        public void insert(int tar){
        }
    }
}

2.具体实现

　　最主要的函数只有两个，insert和compare

　   insert很简单，比如插入 00000110000000000000000000000000（100663296），insert忽略掉最高位符号位，因为所有输入都是正数，则我们从左往右数的

第二位开始

只需要新建节点即可，每个节点的count默认是1（因为一个节点必定在某条路径上，而这条路径代表了一个数，这个数包含从根到这个节点位置形成的前缀(假设这个节点是上图的第四个节点，那么形成的前缀就是 0000 ，00000110000000000000000000000000 包含前缀 0000 )，所以这个节点的count必定 >= 1）。

再插入 00010110000000000000000000000000（369098752）

从根节点出发，如果对应位的节点已经存在，则令其count + +，如果不存在则新建

让当前节点 now 等于 root

因为 369098752 的第二位是 0（忽略最高位符号位第一位），所以 看看 now.child[0] 是否为空，发现不为空，则让now.child[0].count ++

并且让当前节点 等于 now.child[0]，接着向下执行，发现当前节点（节点1）的child[0]也不为空，也让其 count++, 依此类推，到了 now = 节点3

因为 now.child[1] （369098752的第四位为1，所以取1）为空，所以新建节点，并且count 默认 = 1

于是下面有三个count = 2 的节点，表示有两个数的路径包含这些节点

        public void insert(int tar){
            Node now = root;
            root.count ++;
            //从第二位开始，忽略最高为第一位，所有输入都是正数，忽略最高符号位
            for(int i = 30; i >= 0; i --){
                //获取要插入的数的第(32 - i )位
                int res = (tar >>> i) & 1;
                //如果之前不存在节点，则新建节点，count 默认 = 1
                if(now.child[res] == null){
                    now.child[res] = new Node();
                    now = now.child[res];
                }else{
                //如果之前已经有节点存在，则count++
                    now = now.child[res];
                    now.count ++;
                }
            }
        }            

　　compare：

假设某次比较时，字典树如下图状态，并且输入的数Ax如图所示，被比较的数m如下图

为了方便观察，只保留 Ax 和 m 的前面几位

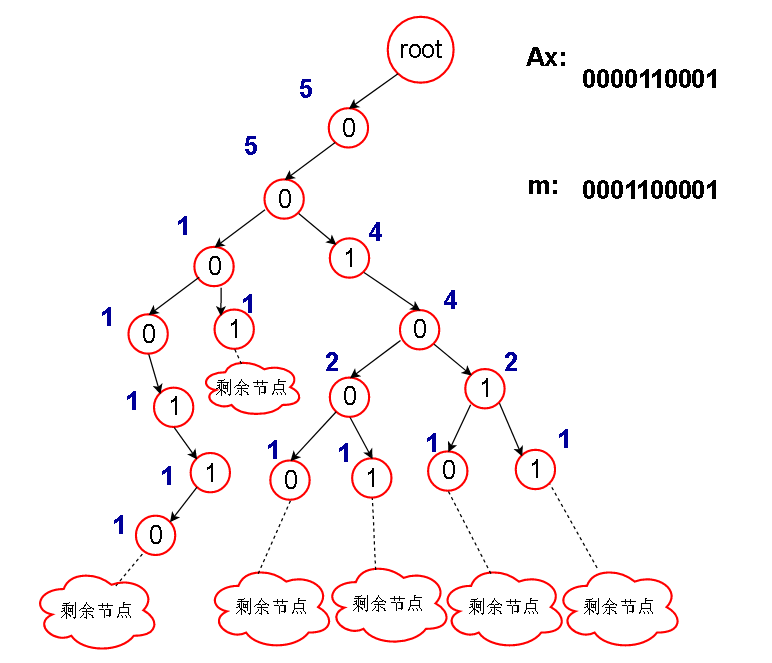
从根节点开始向下比较，也即从第二位开始比较

分如下情况：

1.假设Ax的当前位为 b , 我们的想法当然是想找到 树中当前层次的节点 b ^ 1 ，因为 (b ^ 1) ^ b = 1 ，这样的话，当前位异或的结果为1

如果待比较数m中的当前位为 0，那么Ax和节点 b ^ 1 的所有分支异或的结果都大于m（情况1）

如果待比较数m中的当前位为1，那么目前的比较结果和 m 尚且相等，继续比较下去（情况2）

2.假设 b ^ 1 节点不存在，那么只能委曲求全，走 节点 b，需要注意的是，

如果 m 的当前位为1，说明 m 大于我们能走的唯一路径的全部异或结果（情况3）

因为 b ^ b = 0 < 1 (m 当前位)，说明节点 b 路径上的异或结果都要小于m，而且只能走节点 b 的路径，所以直接返回 0

如果 m 的当前位为0，则目前的比较结果和 m 尚且相等，继续比较下去（情况4）

需要注意的是，情况1不能直接返回节点 b ^ 1 的count，因为另一条路 虽然当前位异或结果 = 0，但是因为 m 的当前位也是0，所以异或结果不至于小于m

还要进行后继比较

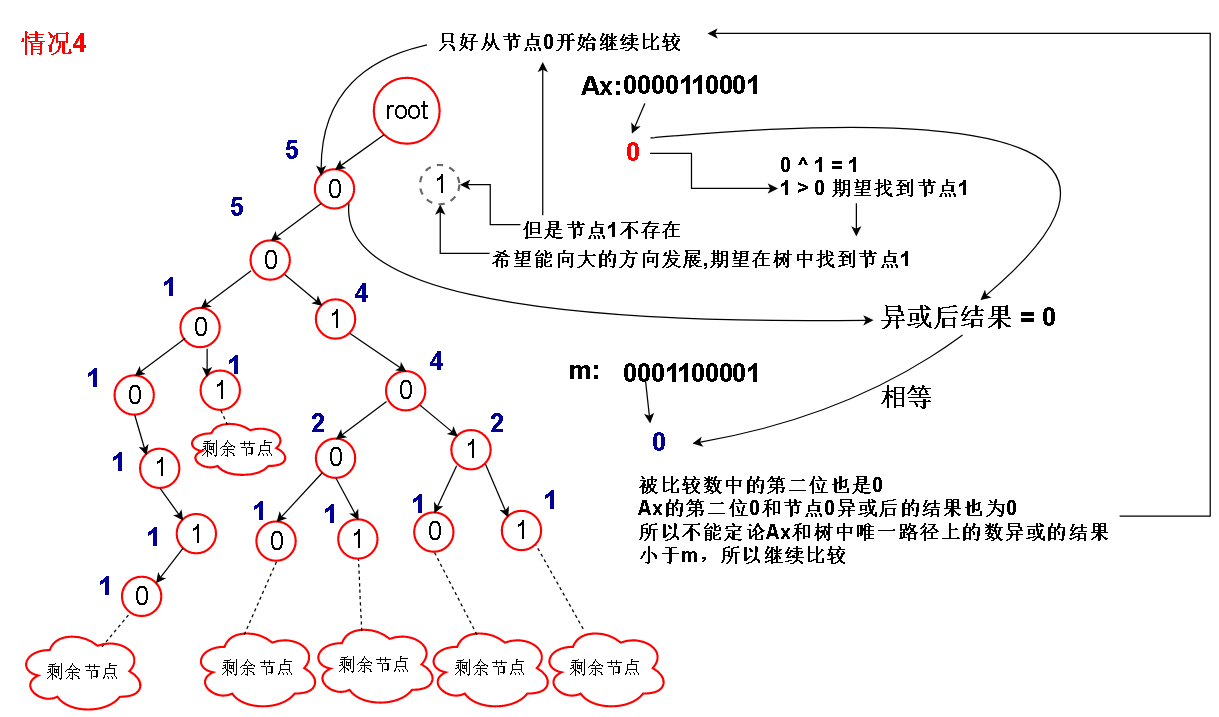
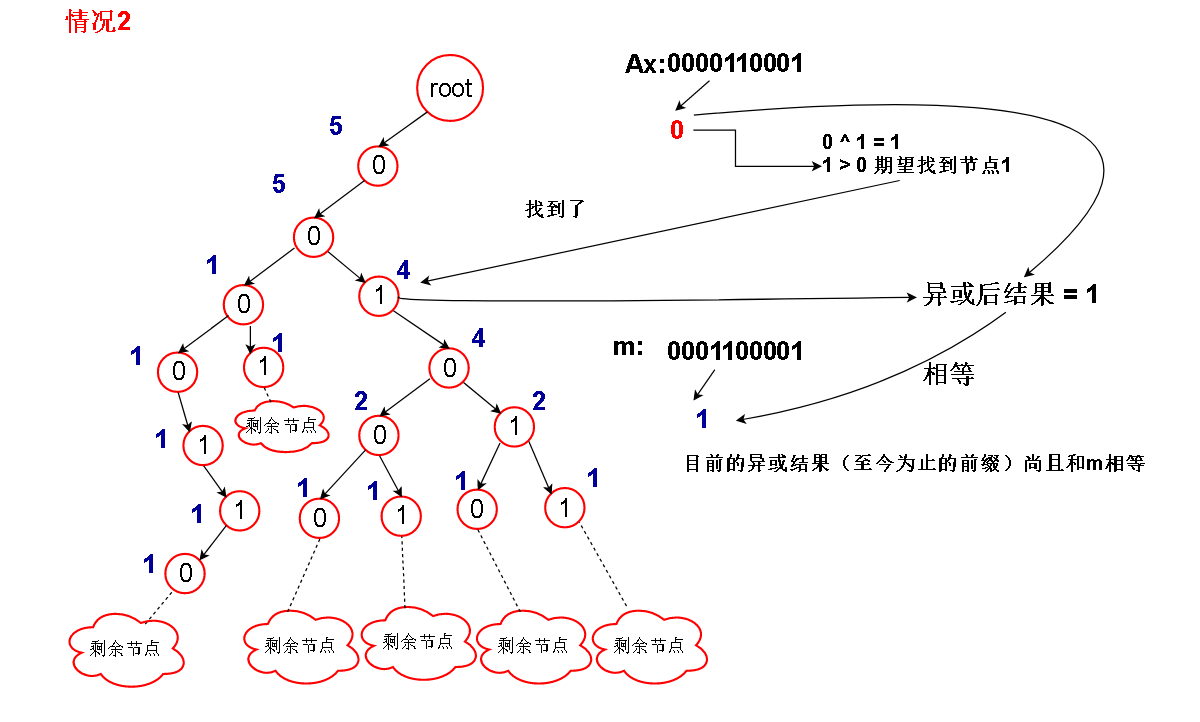
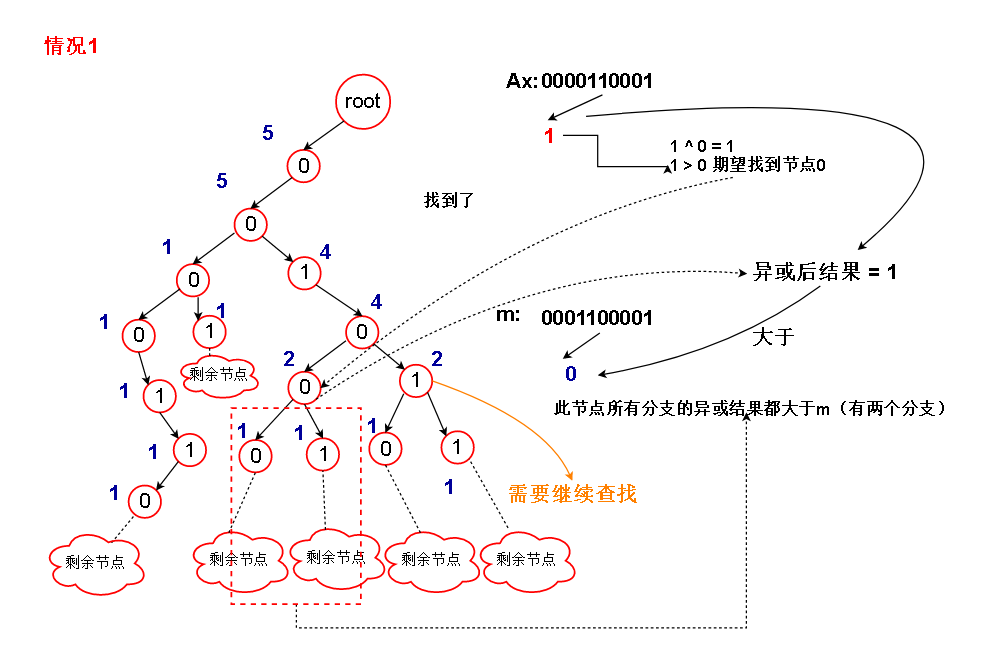
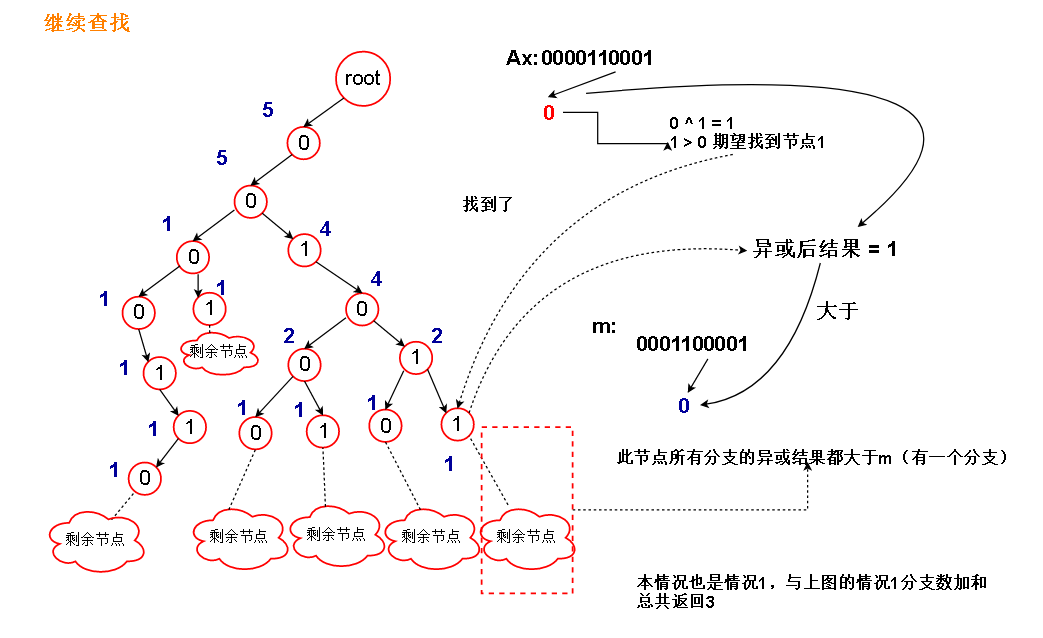
另外，如果当前的节点为空，表明已经比较到叶子节点了，但是还是没有比较出个所以然，说明异或结果与m相等，没有大于m的，返回0(情况5)

 　　　　 // now : 当前前缀树中，需要开始比较的节点
        // tar : 将要插入的数，但是在调用insert插入之前，要和已经插入的数比较（当前前缀树）
        // m : 要大于的那个树
        // bit : 当前节点的儿子们表示的是对第几位的比较
        public int compare(Node now, int Ax, int m, int bit){
            //逐位比较
            for(int i = bit; i >= 0; i --){
                if(now == null){
                    //空节点 表示两者相同 情况5
                    return 0;
                }
                int res = (Ax >>> i) & 1;
                //存在能够 XOR 出 1 的路径, 情况1或2
                if((now.child[res ^ 1]) != null){
                    //如果目标的当前位是 0，说明异或结果已经小于 Ax
                    if(((m >>> i) & 1) == 0){
                        //情况1
　　　　　　　　　　　　　　 //但是不能单纯只返回异或结果大于m的那条路径上的分支数量
                        //因为当前位异或结果相等于m的那条路径上的分支可能还存在满足异或结果大于m的情况
                        return now.child[res ^ 1].count + compare(now.child[res], tar, m, i - 1);
                    } else {
　　　                  //情况2
　　　　　　　　　　　　　　//异或结果相等 接着找
                        now = now.child[res ^ 1];
                    }
                } else{
                    //情况3
                    //异或结果小于 m， 直接返回0
                    if(((m >>> i) & 1) == 1){
                        return 0;
                    }
                    //情况4
　　　　　　　　　　　　//异或结果相等，接着找
                    now = now.child[res];
                }
            }
　　　　　　　//默认返回0
            return 0;
        }

3.结果估计

　  假设输入了 10 ^ 5 个数

　  每个Node对象占用内存 =

　1.没有指针压缩，且在64位机器上

　8字节markOop，8字节 Klass*，8字节数组引用，8字节int(内存对齐)，共32字节

　 每个数占用约32位，每位需要一个节点，且输入了 10 ^ 5 个数，总共占用内存最多 = 10 ^ 5 * 32 * 32 B  = 102 400 KB = 102 MB 左右

　但是实际上字典树中的大部分数都有相同的前缀，真实占用的内存肯定会比 102 MB少不少 （不算上栈上内存）

实际结果：

可见内存占用为 43MB 左右，比102MB小不少。

总结：字典树可以在某些 求最大异或结果或者异或结果如何如何的关于位运算的题目中使用，以减少运算次数，网络IP地址的最长前缀查找等题目同理。