CF877E Danil and a Part-time Job

题目大意: link

有一棵 n 个点的树，根结点为 1 号点，每个点的权值都是 1 或 0

共有 m 次操作，操作分为两种

get 询问一个点 x 的子树里有多少个 1

pow 将一个点 x 的子树中所有节点取反

对于每个 get 给出答案

输入格式：

第一行一个整数 n

第二行共 n−1 个整数，第 i 个数 \(x_i\) 表示 \(x​_i\) 是 i+1 的父亲，

第三行给出每个点的初始权值

第四行一个整数 m

接下来 m 行为操作类型和位置

输入输出样例

输入 #1

4

1 1 1

1 0 0 1

9

get 1

get 2

get 3

get 4

pow 1

get 1

get 2

get 3

get 4

输出 #1

2

0

0

1

2

1

1

0

说明/提示

The tree before the task pow 1.

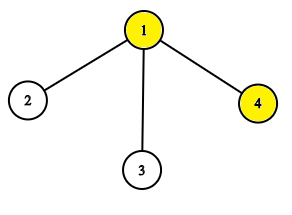
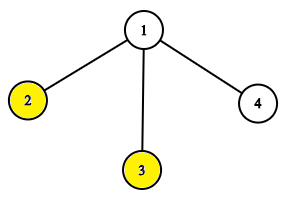
The tree after the task pow 1.

前言

一道很简单的题，当你刷过其他的树剖题，你就会发现这道题是如此的 So,Easy"

题意

两种操作，一个是求子树中 \(1\) 的个数，另一种是区间取反，即 \(0\)变为\(1\)

\(1\)变为\(0\)。（学过树剖的一眼就切了雾）

前置芝士

dfn序

定义： 节点被遍历的顺序

性质： 1. 子树中dfn序是连续的。

   2. 一条重链上dfn序是连续的（~~没学过树剖的请自行跳过~~）

分析

首先，我们可以遍历整棵树，求出每个点的dfn序，在以dfn序建树。

对于操作一，我们可以线段树维护区间和（由性质1可得子树的dfn序是连续的，

所以区间也是连续的）。

对于操作二，我们发现一个序列连续取两次反，就会变为原来的序列。所以我们

维护一个tag标记，1表示未取反，-1表示取反一次。下放时，孩子节点的tag直接

乘以-1就行了，区间和变为区间长度减去原来的区间和。

几个要注意的点

1. 标记要初始化为1，而不是0

2. 下放标记时，孩子节点的标记要乘以-1，而不是变为-1.（因为原来孩子可能

   要取反，现在在取反一次等同于没有取反）。

3. 下放时区间和变为区间长度减去原来的区间和

好像都是打标记出现的问题（雾）

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 2e5+10;
char opt[10];
int n,v,t,x,tot,num;
int dfn[N],w[N],a[N],size[N],head[N];
inline int read()
{
	int s = 0, w = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
	while(ch >= '0' && ch <= '9'){s = s * 10+ch -'0'; ch = getchar();}
	return s * w;
}
struct node{int to,net;}e[N<<1];
void add(int x,int y)
{
	e[++tot].to = y;
	e[tot].net = head[x];
	head[x] = tot;
}
void dfs(int x,int fa)//dfs求dfs序
{
	size[x] = 1; dfn[x] = ++num; w[dfn[x]] = a[x];
	for(int i = head[x]; i; i = e[i].net)
	{
        int to = e[i].to;
        if(to == fa) continue;
        dfs(to,x);
        size[x] += size[to];
	}
}
struct Tree
{
	struct node{
		int lc,rc;
		int tag,sum;
	}tr[N<<2];
	#define l(o) tr[o].lc
	#define r(o) tr[o].rc
	#define tag(o) tr[o].tag
	#define sum(o) tr[o].sum
	void up(int o)
	{
		sum(o) = sum(o<<1) + sum(o<<1|1);
	}
	void cover(int o)
	{
		tag(o) *= -1;
		sum(o) = (r(o) - l(o) + 1) - sum(o);
	}
	void down(int o)//下放标记
	{
		if(tag(o) == -1)
		{
			cover(o<<1); cover(o<<1|1);
			tag(o) = 1;
		}
	}
	void build(int o,int L,int R)
	{
		l(o) = L, r(o) = R; tag(o) = 1;//tag初始化一定要为1
		if(L == R)
		{
			sum(o) = w[L]; return;
		}
		int mid = (L + R)>>1;
		build(o<<1,L,mid);
		build(o<<1|1,mid+1,R);
		up(o);
	}
	void chenge(int o,int L,int R)//区间取反
	{
        if(L <= l(o) && R >= r(o))
        {
        	cover(o); return;
        }
        down(o);
        int mid = (l(o) + r(o))>>1;
        if(L <= mid) chenge(o<<1,L,R);
        if(R > mid) chenge(o<<1|1,L,R);
        up(o);
	}
	int ask(int o,int L,int R)//区间和
	{
		int ans = 0;
		if(L <= l(o) && R >= r(o)) {return sum(o);}
		down(o);
		int mid = (l(o) + r(o))>>1;
		if(L <= mid) ans += ask(o<<1,L,R);
		if(R > mid) ans += ask(o<<1|1,L,R);
		return ans;
	}
}tree;
int main()
{
   n = read();
   for(int i = 2; i <= n; i++)//习惯了从1开始编号
   {
   	   v = read();
   	   add(v,i); add(i,v);
   }
   for(int i = 1; i <= n; i++) a[i] = read();
   dfs(1,1); tree.build(1,1,n);
   t = read();
   while(t--)
   {
   	   scanf("%s",opt+1);
   	   x = read();
   	   if(opt[1] == 'g')//询问子树1的个数
   	   {
   	   	   printf("%d\n",tree.ask(1,dfn[x],dfn[x] + size[x] - 1));
   	   }
   	   if(opt[1] == 'p')//区间取反
   	   {
   	   	   tree.chenge(1,dfn[x],dfn[x] + size[x] - 1);
   	   }
    }
    return 0;
}

ENDING