2019牛客暑期多校训练营（第一场）E ABBA （DP/卡特兰数）

传送门

知识点：卡特兰数/动态规划

法一：动态规划

由题意易知字符串的任何一个前缀都满足\(cnt(A) - cnt(B) \le n , cnt(B)-cnt(A)\le m\)

\(d[i][j]\) 表示前\(i\) 个字符，有 \(j\) 个\(A\) ，有\(i-j\) 个\(B\) 的方案数

• \(d[0][0] = 1,d[2*n+2*m][n+m] 为答案\)
• 当\(j-(i-j)\le n,(i-j)-j\le m\) 时，\(d[i][j] = d[i-1][j] + d[i-1][j-1]\)

#include <bits/stdc++.h>
using namespace std;
const int mod = 1e9+7;
typedef long long ll;
int n,m;
ll d[4010][2010];
int main(){
    while(~scanf("%d%d",&n,&m)){
        d[0][0] = 1;
        for(int i=1;i<=2*(n+m);i++){
            for(int j=0;j<=i && j <= (n+m);j++){
                int a = j;
                int b = i - j;
                if(a - b > n || b - a > m)continue;
                d[i][j] = (d[i-1][j] + d[i-1][j-1])%mod;
            }
        }
        printf("%lld\n",d[2*(n+m)][(n+m)]);
        for(int i=1;i<=2*(n+m);i++){
            for(int j=0;j<=i && j <=(n+m);j++)
                d[i][j] = 0;
        }
    }
    return 0;
}

法二：组合数学

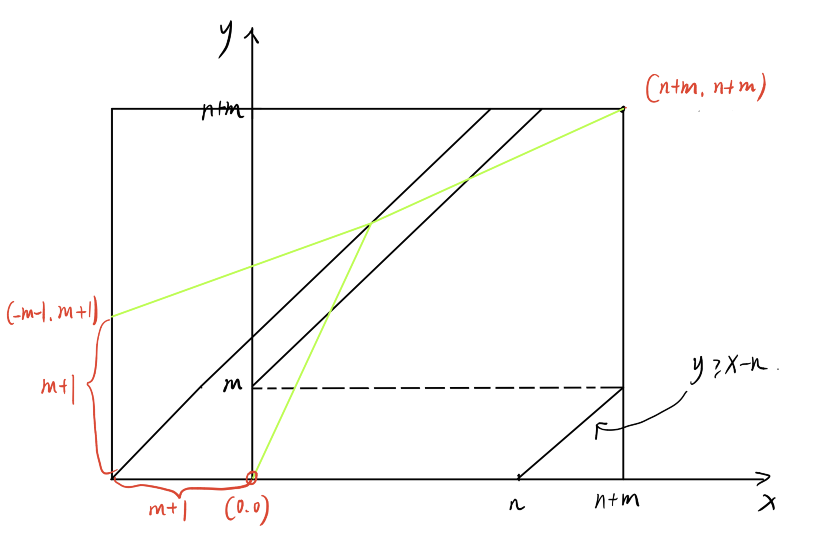
设\(x\) 为A的个数，\(y\)为B的个数，那么由\((0,0)\rightarrow (n+m,n+m)\)的路径上面必须满足\(x-y\le n,y-x\le m\) 两个条件。

在经典的卡特兰数路径计数问题中就有提到，详情请参考：https://oi-wiki.org/math/catalan/

将上面两个限制放在图中就是两个直线，然后求起点到终点的非降路径方案数（非降的意思是x和y不能变小），先考虑偏上的那条线（下面同理可得），如果我们有一条路径越过了\(y=x+m\) 这条线，那么该路径上面一定会有一个点在\(y=x+m+1\)这条线上。

从上图中不难看出来，这样的路径等效于从\((-m-1,m+1)\)到\((n+m,n+m)\) 的路径，因为\((0,0)与(-m-1,m+1)关于y=x+m+1 对称\)。

又

1. \((0,0)\rightarrow (n+m,n+m)\) 的所有非降路径数为\(C_{2n+2m}^{n+m}\)
2. \((-m-1,m+1)\rightarrow (n+m,n+m) 的所有非降路径数为\)C_{2n+2m}^{n-1}$
3. \((n+1,-n-1)\rightarrow (n+m,n+m)\) 的所有非降路径数位\(C_{2n+2m}^{m-1}\)

所以总答案为\(C_{2n+2m}^{n+m}-C_{2n+2m}^{n-1}-C_{2n+2m}^{m-1}\)

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 10010;
const int p = 1e9+7;
ll jc[N],inv[N];
int n,m;
ll ksm(ll a,ll b){
    ll res = 1;
    for(;b;b >>= 1){
        if(b & 1)res = res * a % p;
        a = a * a % p;
    }
    return res;
}
ll C(int a,int b){
    return jc[a] * inv[b] % p * inv[a-b] % p;
}
int main(){
    jc[0] = inv[0] = 1;
    for(int i=1;i<=4000;i++)jc[i] = jc[i-1] * i % p,inv[i] = ksm(jc[i],p-2);
    while(~scanf("%d%d",&n,&m)){
        int s = 2*(n+m);
        printf("%lld\n",(C(s,s/2) - (C(s,n-1) + C(s,m-1))%p + p) % p);
    }
    return 0;
}