洛谷——P2784 化学1（chem1）- 化学合成

P2784 化学1（chem1）- 化学合成

题目背景

蒟蒻HansBug在化学考场上，挠了无数次的头，可脑子里还是一片空白。

题目描述

眼下出现在蒟蒻HansBug面前的是一个化学合成题，据他所知，一般答案如下面这样的格式：

（接下一行）

简单解释下：每种化合物可以通过一步反应生成另一个化合物（将这称作一步反应，设为 A--->B），现在假设每个A--->B中，理论上1个单位的A都仅可以生成1个单位的B。然而实际实验表明，并不存在绝对完全的化学转化，设转化率为C（即1个单位A实际可以生成C个单位的B，0<C<1）。

现在蒟蒻HansBug的知识体系中有N个这样A--->B的转化。然而题目中蒟蒻HansBug要由1个单位的化合物S生成化合物T，可是他脑细胞和RP已经消耗殆尽，所以找到最终产量最高的合成路线的艰巨任务就交给你啦！

输入输出格式

输入格式：

第一行为4个整数：N、M、S、T，分别表示总共出现的化合物个数、HansBug所知道的反应个数、起始的化合物序号、终末的化合物序号。（1<=S、T<=N）

第2-M+1行每行为两个整数和一个实数：Ai、Bi、Ci，分别表示第i个反应为由1个单位的Ai化合物生成Ci单位的Bi化合物。

输出格式：

一行，包含一个实数，为最佳路线下最终的产量（四舍五入保留4位小数），如果没有可行路线的话，输出orz。

输入输出样例

输入样例#1： 复制

3 3 1 3
1 3 0.8
1 2 0.9
2 3 0.9

输出样例#1： 复制

0.8100

输入样例#2： 复制

3 3 2 1
1 3 0.8
1 2 0.9
2 3 0.9

输出样例#2： 复制

orz

说明

样例1和样例2中，两条合成路线分别为1--->3、1--->2、2--->3，产率分别为0.8、0.9、0.9。

在样例1中，有两种可行的路线1--->3和1--->2--->3，最终产量分别为0.8、0.9*0.9=0.81，故第二条路线更优，产量为0.8100。

样例2中，2只能生成3，3无法生成别的化合物，故无法生成，蒟蒻HansBug只好选择orz。

样例数据：

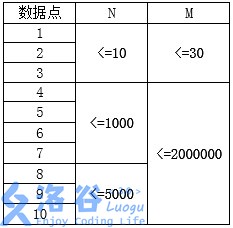
spfa求最长路

#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 1000100
#define maxn 9999999
using namespace std;
queue<int>q;
bool vis[N];
double z,dis[N];
int n,m,a,b,x,y,tot,head[N];
int read()
{
    ,f=; char ch=getchar();
    ;ch=getchar();}
    +ch-',ch=getchar();
    return x*f;
}
struct Edge
{
    int to,next;
    double dis;
}edge[N*];
int add(int x,int y,double z)
{
    tot++;
    edge[tot].to=y;
    edge[tot].dis=z;
    edge[tot].next=head[x];
    head[x]=tot;
}
int spfa(int s)
{
//    for(int i=1;i<=n;i++) dis[i]=0;
    dis[s]=,vis[s]=;q.push(s);
    while(!q.empty())
    {
        x=q.front(),q.pop();vis[x]=false;
        for(int i=head[x];i;i=edge[i].next)
        {
            int t=edge[i].to;
            if(dis[t]<dis[x]*edge[i].dis)
            {
                dis[t]=dis[x]*edge[i].dis;
                if(!vis[t]) vis[t]=true,q.push(t);
            }
        }
    }
}
int main()
{
    n=read(),m=read(),a=read(),b=read();
    ;i<=m;i++)
    {
        x=read(),y=read();
        scanf("%lf",&z);
        add(x,y,z);
    }
    spfa(a);
    ) printf("orz");
    else printf("%.4lf",dis[b]);
    ;
}