概率dp学习记录

论文参考 汤可因《浅谈一类数学期望问题的解决方法》

反正是很神奇的东西吧。。我脑子不好不是很能想得到。

bzoj 1415

1415: [Noi2005]聪聪和可可

Time Limit: 10 Sec  Memory Limit: 162 MB
Submit: 2140  Solved: 1258
[Submit][Status][Discuss]

Description

Input

数据的第1行为两个整数N和E，以空格分隔，分别表示森林中的景点数和连接相邻景点的路的条数。 第2行包含两个整数C和M，以空格分隔，分别表示初始时聪聪和可可所在的景点的编号。 接下来E行，每行两个整数，第i+2行的两个整数Ai和Bi表示景点Ai和景点Bi之间有一条路。 所有的路都是无向的，即：如果能从A走到B，就可以从B走到A。 输入保证任何两个景点之间不会有多于一条路直接相连，且聪聪和可可之间必有路直接或间接的相连。

Output

输出1个实数，四舍五入保留三位小数，表示平均多少个时间单位后聪聪会把可可吃掉。

Sample Input

【输入样例1】
4 3
1 4
1 2
2 3
3 4
【输入样例2】
9 9
9 3
1 2
2 3
3 4
4 5
3 6
4 6
4 7
7 8
8 9

Sample Output

【输出样例1】
1.500
【输出样例2】
2.167

 

---

 

论文题。。自己看看论文就懂了。

 

 

 

 

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define clr_1(x) memset(x,-1,sizeof(x))
 #define INF 0x3f3f3f3f
 #define mod 1000000009
 #define LL long long
 #define next nexted
 using namespace std;
 const int N=1e3+;
 int ans[N][N],vis[N],step[N][N];
 double f[N][N];
 int u,v,m,n,pu,pv;
 vector<int> edge[N];
 void bfs(int root)
 {
     int now,p;
     clr(vis);
     queue<int> que;
     step[root][root]=root;
     vis[root]=;
     for(int i=;i<edge[root].size();i++)
     {
         p=edge[root][i];
         que.push(p);
         step[root][p]=p;
         vis[p]=;
     }
     while(!que.empty())
     {
         now=que.front();
         que.pop();
         for(int i=;i<edge[now].size();i++)
         {
             p=edge[now][i];
             if(!vis[p])
             {
                 que.push(p);
                 vis[p]=;
                 step[root][p]=step[root][now];
             }
         }
     }
     return ;
 }
 double Find(int u,int v)
 {
     if(u==v)
         return f[u][v]=;
     if(f[u][v]>)
         return f[u][v];
     if(step[u][v]==v)
         return f[u][v]=;
     if(step[step[u][v]][v]==v)
         return f[u][v]=;
     int p;
     for(int i=;i<edge[v].size();i++)
     {
         p=edge[v][i];
         f[u][v]+=Find(step[step[u][v]][v],p);
     }
     f[u][v]+=Find(step[step[u][v]][v],v);
     f[u][v]=f[u][v]/(edge[v].size()+)+;
     return f[u][v];
 }
 int main()
 {
     scanf("%d%d",&n,&m);
     scanf("%d%d",&u,&v);
     for(int i=;i<=m;i++)
     {
         scanf("%d%d",&pu,&pv);
         edge[pu].push_back(pv);
         edge[pv].push_back(pu);
     }
     for(int i=;i<=n;i++)
         sort(edge[i].begin(),edge[i].end());
     for(int i=;i<=n;i++)
         bfs(i);
     printf("%.3f\n",Find(u,v));
     return ;
 }

bzoj 2685

2685: Sgu385 highlander

Time Limit: 10 Sec  Memory Limit: 128 MBSec  Special Judge
Submit: 112  Solved: 64
[Submit][Status][Discuss]

Description

一个游戏N个人，每个人开始一张卡片，上面写着N个人中某个人的名字。
每张卡片上的名字都不同，且不会拿到自己名字的卡片。
游戏开始时，每个人开始追自己卡片上写着的人，如果A有写着B的卡片。
当A追到B后，A可以拿到所有B的卡片。如果每个人都没人可追，游戏结束。
这时开始数每个人手上的卡片总数，获得卡片最多的人即是胜者。如果有多个人
的卡片一样多，则都是胜者。现想知道有多少人在理论上有概论成为胜者。

Input

输入一个整数N　２<=N<=100

Output

一个实数

Sample Input

2

Sample Output

2

HINT

你的答案与标准答案的差不超过10^-9

Source

---

同样的一道论文题。

这个题目我们可以把这些错排看成一张有向图。由于每个点出入度为1，且不会指向自己。所以这是一个多个不相交的环，并且不存在自环（这个很重要，公式推导的时候环长度>1）组成的图。

那我们看看数据范围n≤100，所以能接受O(n³)的算法。

于是我们做这么一个三维的推导：

f[i][j][k]代表有i个点确定，其中最长的环长度为j，且长度为j的环数量为k的情况数量，K也为获胜人数。

如果我们只形成一个长度为j的环，他的情况数量为A(n,j)/j，n为剩余点的数量。

如果我们k个长度为j的环，他的情况数量为(A(n,j)*A(n-j,j)*A(n-2*j,j)……A(n-(k-1)*j,j))/A(j,j)，n为剩余点数量。因为A(j,j)==j!==1*2*3……*j，所以我们从k=1推到k=n的时候f[i][j][k]=f[i-j][j][k-1]*A(n-(i-j),j)/j。

然后g[i][j]代表i个点确定，最长环长度为j的情况数量，即把k那一维求和。

可得出以下公式：

答案分母为情况总数，即错排总数，可以通过错排递推式得到：

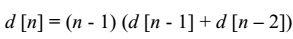
他是所有和项的分母。他和上面的j*f[i][j][k]形成每种获胜人数下的权（概率）。

然后j*k是每种情况的下获胜人数，就是环里所有人都可能赢，没毛病。

相当于运用全概率公式E(K)=E(E(K|J)=|J=1)+E(K|J=2)……E(K|J=n)

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define clr_1(x) memset(x,-1,sizeof(x))
 #define mod 1000000007
 #define LL long long
 #define INF 0x3f3f3f3f
 using namespace std;
 const int N=1e2+;
 double f[N][N][N],g[N][N];
 double pre[],ans;
 double jc[N];
 int n,m,T,p;
 double a(int n,int m)
 {
     return n>=m?jc[n]/jc[n-m]:;
 }
 int main()
 {
     scanf("%d",&n);
     pre[]=pre[]=;
     pre[]=;
     for(int i=;i<=n;i++)
         pre[i%]=(i-)*(pre[(i-)%]+pre[(i-)%]);
     jc[]=jc[]=;
     for(int i=;i<=n;i++)
         jc[i]=jc[i-]*i;
     for(int i=;i<=n;i++)
     {
         for(int j=;j<i;j++)
         {
             p=min(i-j,j-);
             for(int k=;k<=p;k++)
                 f[i][j][]+=g[i-j][k];
             f[i][j][]*=a(n-i+j,j)/j;
             g[i][j]=f[i][j][];
             p=i/j;
             for(int k=;k<=p;k++)
                 g[i][j]+=(f[i][j][k]=f[i-j][j][k-]*a(n-i+j,j)/j/k);
         }
         f[i][i][]=g[i][i]=a(n,i)/i;
     }
     for(int i=;i<=n;i++)
     {
         p=n/i;
         for(int j=;j<=p;j++)
             ans+=f[n][i][j]*j*i;
     }
     ans/=pre[n%];
     printf("%.10f\n",ans);
 }

bzoj 1419

1419: Red is good

Time Limit: 10 Sec  Memory Limit: 64 MB
Submit: 1210  Solved: 560
[Submit][Status][Discuss]

Description

桌面上有R张红牌和B张黑牌，随机打乱顺序后放在桌面上，开始一张一张地翻牌，翻到红牌得到1美元，黑牌则付

出1美元。可以随时停止翻牌，在最优策略下平均能得到多少钱。

Input

一行输入两个数R,B,其值在0到5000之间

Output

在最优策略下平均能得到多少钱。

Sample Input

5 1

Sample Output

4.166666

HINT

输出答案时,小数点后第六位后的全部去掉,不要四舍五入.

Source

 

---

 

这个人的决策只有两种：翻开牌和不翻开牌。所谓的最优策略。。还有什么最优?当然是期望得到的钱最优啊。因此在I张R和J张B的情况下，如果我们翻牌的期望>0也就是还能拿钱的情况下我们选择继续翻牌来获得金钱。反之不翻牌，期望为0。

设f[i,j]表示还剩I张R牌和J张B牌的期望，边界条件是f[i,0]=f[i-1,0]+1,f[0,j]=0。转移方程是$f[i][j]=(f[i-1][j]+1)*\frac{i}{i+j}+(f[i][j-1]-1)*\frac{j}{i+j}$。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define clr_1(x) memset(x,-1,sizeof(x))
 #define mod 1000000007
 #define LL long long
 #define INF 0x3f3f3f3f
 using namespace std;
 const int N=5e3+;
 int n,m;
 double f[][N];
 int main()
 {
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++)
     {
         f[i&][]=f[i&^][]+;
         for(int j=;j<=m;j++)
             f[i&][j]=max(0.0,((f[i&][j-]-)*j+(f[i&^][j]+)*i)/(i+j));
     }
     printf("%.6f\n",((LL)(f[n&][m]*))*1.0/);
 }