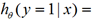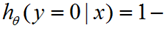softmax回归(理论部分解释)
前面我们已经说了logistic回归,训练样本是
,
(且这里的
是d维,下面模型公式的x是d+1维,其中多出来的一维是截距横为1,这里的y=±1也可以写成其他的值,这个无所谓不影响模型,只要是两类问题就可以),训练好这个模型中
参数θ以后(或者是
这个模型,这俩是一个模型),然后给入一个新的
,我们就可以根据模型来预测
对应label=1或0的概率了。
前面处理的是两类问题,我们想把这个两类问题扩展,即根据训练好的模型,给入一个新的
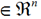 ,我们就可以根据模型来预测
,我们就可以根据模型来预测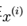 对应label=1,2,…k等多个值的概率。我们首先也是最重要的部分是确定这个新的模型是什么。对于一个x,新的模型
对应label=1,2,…k等多个值的概率。我们首先也是最重要的部分是确定这个新的模型是什么。对于一个x,新的模型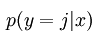 (j=1,2..k)要加起来等于1.
(j=1,2..k)要加起来等于1.
我们假设新模型为:
 ……………………………………..……………………………………………………………………(1)
……………………………………..……………………………………………………………………(1)
(这里模型中的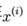 是经过前面的
是经过前面的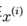 处理后的,每一个
处理后的,每一个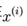 都增加了一维
都增加了一维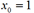 )
)
其中 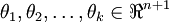 是模型的参数在实现Softmax回归时,将
是模型的参数在实现Softmax回归时,将  用一个
用一个 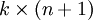 的矩阵来表示会很方便,该矩阵是将
的矩阵来表示会很方便,该矩阵是将 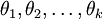 按行罗列起来得到的,如下所示:
按行罗列起来得到的,如下所示:
这里说一个问题:在logistic回归中,是两类问题,我们只用了一个θ,这里我们是不是也可以只用k-1个θk就可以表示所有的模型呢?具体就是我们只需要把 置为0.所以
置为0.所以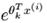 =1,这样带入公式(1)中就可以少使用一个
=1,这样带入公式(1)中就可以少使用一个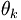 ,我们验证一下,如果k=2即两类问题时,这个模型就退化成logistic回归,我们令θ2=0,那么我们得到:
,我们验证一下,如果k=2即两类问题时,这个模型就退化成logistic回归,我们令θ2=0,那么我们得到:
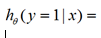
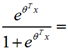
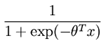 ,
,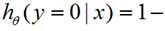
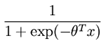 ,得证。所以说我们的
,得证。所以说我们的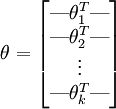 参数矩阵确实存在参数冗余,这个问题,下面还会继续说。
参数矩阵确实存在参数冗余,这个问题,下面还会继续说。
接下来我们要做的是求cost function:
我们知道logistic的cost function(不加约束项)为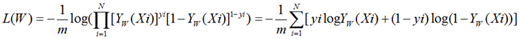 ,即把每个样本
,即把每个样本 带入其label
带入其label  对应的模型公式里(
对应的模型公式里( 的label
的label 是1,就把
是1,就把 代入
代入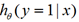 ,是0就代入
,是0就代入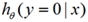 ),然后把所有样本
),然后把所有样本 带入模型得到的结果相乘再取对数log(对数运算也就是每个样本
带入模型得到的结果相乘再取对数log(对数运算也就是每个样本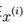 带入模型得到的结果再相加),取平均。我们这里同样这样做,只是因为这里类别计较多,我们使用一个”示性函数‘’来使公式表达整洁:
带入模型得到的结果再相加),取平均。我们这里同样这样做,只是因为这里类别计较多,我们使用一个”示性函数‘’来使公式表达整洁:
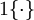 是示性函数,其取值规则为:
是示性函数,其取值规则为: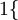 值为真的表达式
值为真的表达式 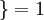 ,
, 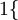 值为假的表达式
值为假的表达式 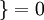 。
。
举例来说,表达式 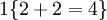 的值为1 ,
的值为1 ,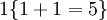 的值为 0。
的值为 0。
我们的代价函数为(不加约束项):
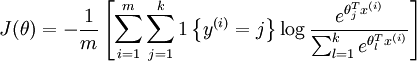
我们知道对logistic回归模型的cost function 最小化,这里以梯度下降法进行说明:
这里的θ是一个k*(n+1)的矩阵,对应着模型里面的所有参数,我们现在有一个θ参数矩阵值
,那么我们通过梯度下降法得到的新的θ’参数矩阵值是多少呢,怎么求?是这样的,比如我们更新θ(1,1)这个参数目前对应的值,
首先我们求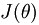 对θ(1,1)这一个参数的偏导:
对θ(1,1)这一个参数的偏导:
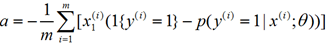 求导得到的是一个数(即把所有
求导得到的是一个数(即把所有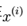 和目前的θ参数矩阵值带入左边这个公式得到的结果即是,而不是还需要θ的第一个元素增加一个增量什么的,因为这里已经对θ(1,1)求导了)。有的地方是按梯度更新的,梯度是一个向量,但梯度也是分别对每一个参数求导得到的数,然后组成的向量。这里这么写是为了便于理解(在程序中还是以矩阵运算进行的,所以跟这个公式会有出入,但是核心思想是一样的)。然后新的θ’参数矩阵值的第一个元素θ’(1,1)=θ(1,1)-a。然后利用同样的方法
和目前的θ参数矩阵值带入左边这个公式得到的结果即是,而不是还需要θ的第一个元素增加一个增量什么的,因为这里已经对θ(1,1)求导了)。有的地方是按梯度更新的,梯度是一个向量,但梯度也是分别对每一个参数求导得到的数,然后组成的向量。这里这么写是为了便于理解(在程序中还是以矩阵运算进行的,所以跟这个公式会有出入,但是核心思想是一样的)。然后新的θ’参数矩阵值的第一个元素θ’(1,1)=θ(1,1)-a。然后利用同样的方法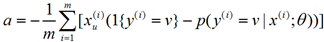 得到新的参数矩阵值θ’的其他元素θ’(v,u)。我们得到θ’后,我们按这种方法再次迭代得到新的参数矩阵值θ”…..最后得到使
得到新的参数矩阵值θ’的其他元素θ’(v,u)。我们得到θ’后,我们按这种方法再次迭代得到新的参数矩阵值θ”…..最后得到使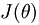 收敛的模型参数。
收敛的模型参数。
这时候我们讨论一下前面提到的参数冗余问题:
现在我们模型的参数矩阵θ求好了,那么我们有一个样本 ,我们想求下这个样本对应的label等于各个i(i=1,2…k)的概率即利用
,我们想求下这个样本对应的label等于各个i(i=1,2…k)的概率即利用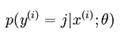 。
。
这时候我们让矩阵θ的每一行 都变成
都变成 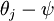 (
(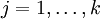 )。那么对任意的j,j∈
)。那么对任意的j,j∈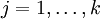 ,有
,有
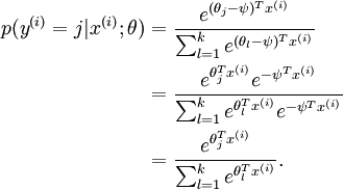
也就是说参数矩阵θ的每一行 都减去减去某一个常向量
都减去减去某一个常向量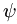 得到新的参数矩阵θ’,那么这两个参数矩阵是等价的,即一个样本
得到新的参数矩阵θ’,那么这两个参数矩阵是等价的,即一个样本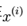 对应的label等于各个i(i=1,2…k)的概率在两个参数矩阵下是一样的。这时候我们假设如果参数
对应的label等于各个i(i=1,2…k)的概率在两个参数矩阵下是一样的。这时候我们假设如果参数 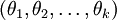 是代价函数
是代价函数  的极小值点,那么
的极小值点,那么 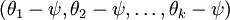 同样也是它的极小值点,其中
同样也是它的极小值点,其中 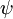 可以为任意向量。因此使
可以为任意向量。因此使  最小化的解不是唯一的。(有趣的是,由于
最小化的解不是唯一的。(有趣的是,由于  仍然是一个凸函数,如果是只是用梯度下降法的话,不会遇到局部最优解的问题。但是 Hessian 矩阵是奇异的/不可逆的,这会直接导致采用牛顿法优化就遇到数值计算的问题,所以我们还是要寻找在使用梯度下降、牛顿法或其他算法时都可以解决参数冗余所带来的数值问题的办法)
仍然是一个凸函数,如果是只是用梯度下降法的话,不会遇到局部最优解的问题。但是 Hessian 矩阵是奇异的/不可逆的,这会直接导致采用牛顿法优化就遇到数值计算的问题,所以我们还是要寻找在使用梯度下降、牛顿法或其他算法时都可以解决参数冗余所带来的数值问题的办法)
这时候我们可以考虑这个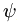 等于某一个
等于某一个 ,那么这个
,那么这个 就变成了0向量,这样新的参数矩阵就少了一组变量,只需要k-1组
就变成了0向量,这样新的参数矩阵就少了一组变量,只需要k-1组 ,我们就可以构建模型,这样我们的cost function的优化结果只有唯一解。并且在logistic公式中我们也是这么做的,前面已经证明了。
,我们就可以构建模型,这样我们的cost function的优化结果只有唯一解。并且在logistic公式中我们也是这么做的,前面已经证明了。
在实际应用中,为了使算法实现更简单清楚,往往保留所有参数  ,而不任意地将某一参数设置为 0。但此时我们需要对代价函数做一个改动:加入权重衰减。权重衰减可以解决 softmax 回归的参数冗余所带来的数值问题。
,而不任意地将某一参数设置为 0。但此时我们需要对代价函数做一个改动:加入权重衰减。权重衰减可以解决 softmax 回归的参数冗余所带来的数值问题。
我们通过添加一个权重衰减项 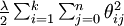 来修改代价函数,这个衰减项会惩罚过大的参数值,现在我们的代价函数变为:
来修改代价函数,这个衰减项会惩罚过大的参数值,现在我们的代价函数变为:
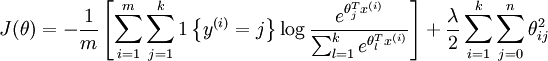
- 那为什么加入这个权重衰减项也就是L2正则项后,就可以解决参数冗余所带来的数值问题?
有了这个权重衰减项以后 (
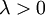
- ),代价函数就变成了严格的凸函数,这样就可以保证得到唯一的解了。 此时的 Hessian矩阵变为可逆矩阵,并且因为

- 是凸函数,梯度下降法和 L-BFGS 等算法可以保证收敛到全局最优解。
在优化参数每次迭代得到新的θ‘时,与前面的相比,我们这里只要需要改变上面的a,即上面的a还要加上一个数。你要更新θ元素的某个元素θ(v,u),就是把对应的a变成:a加上正则项权重lamuda倍的原参数矩阵对应的元素θ(v,u),从而得到a’,然后更新θ’(v,u)=θ(v,u)-迭代速率α倍的a’。
softmax回归(理论部分解释)的更多相关文章
- DNN:逻辑回归与 SoftMax 回归方法
UFLDL Tutorial 翻译系列:http://deeplearning.stanford.edu/wiki/index.php/UFLDL_Tutorial 第四章:SoftMax回归 简介: ...
- 机器学习之线性回归---logistic回归---softmax回归
在本节中,我们介绍Softmax回归模型,该模型是logistic回归模型在多分类问题上的推广,在多分类问题中,类标签 可以取两个以上的值. Softmax回归模型对于诸如MNIST手写数字分类等问题 ...
- 机器学习 —— 基础整理(五)线性回归;二项Logistic回归;Softmax回归及其梯度推导;广义线性模型
本文简单整理了以下内容: (一)线性回归 (二)二分类:二项Logistic回归 (三)多分类:Softmax回归 (四)广义线性模型 闲话:二项Logistic回归是我去年入门机器学习时学的第一个模 ...
- 线性回归、Logistic回归、Softmax回归
线性回归(Linear Regression) 什么是回归? 给定一些数据,{(x1,y1),(x2,y2)…(xn,yn) },x的值来预测y的值,通常地,y的值是连续的就是回归问题,y的值是离散的 ...
- UFLDL深度学习笔记 (二)SoftMax 回归(矩阵化推导)
UFLDL深度学习笔记 (二)Softmax 回归 本文为学习"UFLDL Softmax回归"的笔记与代码实现,文中略过了对代价函数求偏导的过程,本篇笔记主要补充求偏导步骤的详细 ...
- 1.线性回归、Logistic回归、Softmax回归
本次回归章节的思维导图版总结已经总结完毕,但自我感觉不甚理想.不知道是模型太简单还是由于自己本身的原因,总结出来的东西感觉很少,好像知识点都覆盖上了,但乍一看,好像又什么都没有.不管怎样,算是一次尝试 ...
- Haskell手撸Softmax回归实现MNIST手写识别
Haskell手撸Softmax回归实现MNIST手写识别 前言 初学Haskell,看的书是Learn You a Haskell for Great Good, 才刚看到Making Our Ow ...
- 小白学习之pytorch框架(4)-softmax回归(torch.gather()、torch.argmax()、torch.nn.CrossEntropyLoss())
学习pytorch路程之动手学深度学习-3.4-3.7 置信度.置信区间参考:https://cloud.tencent.com/developer/news/452418 本人感觉还是挺好理解的 交 ...
- Softmax回归
Reference: http://ufldl.stanford.edu/wiki/index.php/Softmax_regression http://deeplearning.net/tutor ...
随机推荐
- 报错:PermissionError: [WinError 5] Access is denied: 'C:\\Program Files\\Anaconda3\\Lib\\site-packages\\pywebhdfs'
Outline 在本(Windows系统)地往 “PAI”(hdfs)上上传数据时,需要安装pywebhdfs包,然后就报错了: 报错信息: PermissionError: [WinError 5] ...
- PHP获取客户端的IP
function getClientIP(){ global $ip; if (getenv("HTTP_CLIENT_IP")) $ip = geten ...
- error:No resource found that matches the given name 'Theme.AppCompat.Light'
一.stsckoverflow http://stackoverflow.com/questions/17870881/cant-find-theme-appcompat-light-for-new- ...
- django 中模板语言的各种用法
模板 1.视图中使用模板 模版的创建过程,对于模版,其实就是读取模版(其中嵌套着模版标签),然后将 Model 中获取的数据插入到模版中,最后将信息返回给用户 1.普通方法:HTML被直接硬编码在 P ...
- Spark学习笔记--安装SCALA和IDEA开发环境
一:安装Scala
- 中文Appium API 文档
该文档是Testerhome官方翻译的源地址:https://github.com/appium/appium/tree/master/docs/cn官方网站上的:http://appium.io/s ...
- Vue.js——框架
一.什么是VUE vue 是一个构建用户界面的javascript框架 特点:轻量,高效 特性:双向数据绑定,数据驱动视图 二.vue的使用 1.引入vue.js <script src=vue ...
- begoo——对象的CRUD操作
如果已知主键的值,那么可以使用这些方法进行CRUD操作 对object操作的四个方法Read/Insert/Update/Delete o := orm.NewOrm() user := new(Us ...
- 解释一下python中的赋值运算符
我们将所有的算术运算符和赋值运算符号放在一起展示 a=7 a+=1 print(a) a-=1 print(a) a*=2 print(a) a/=2 print(a) a**=2 print(a) ...
- Building an FTP Test Plan
参考:http://jmeter.apache.org/usermanual/build-ftp-test-plan.html 1.创建一个线程组 2.线程组--->添加--->配置元件- ...