洛谷P2860 [USACO06JAN]冗余路径Redundant Paths

题目描述

In order to get from one of the F (1 <= F <= 5,000) grazing fields (which are numbered 1..F) to another field, Bessie and the rest of the herd are forced to cross near the Tree of Rotten Apples. The cows are now tired of often being forced to take a particular path and want to build some new paths so that they will always have a choice of at least two separate routes between any pair of fields. They currently have at least one route between each pair of fields and want to have at least two. Of course, they can only travel on Official Paths when they move from one field to another.

Given a description of the current set of R (F-1 <= R <= 10,000) paths that each connect exactly two different fields, determine the minimum number of new paths (each of which connects exactly two fields) that must be built so that there are at least two separate routes between any pair of fields. Routes are considered separate if they use none of the same paths, even if they visit the same intermediate field along the way.

There might already be more than one paths between the same pair of fields, and you may also build a new path that connects the same fields as some other path.

为了从F(1≤F≤5000)个草场中的一个走到另一个，贝茜和她的同伴们有时不得不路过一些她们讨厌的可怕的树．奶牛们已经厌倦了被迫走某一条路，所以她们想建一些新路，使每一对草场之间都会至少有两条相互分离的路径，这样她们就有多一些选择．

每对草场之间已经有至少一条路径．给出所有R(F-1≤R≤10000)条双向路的描述，每条路连接了两个不同的草场，请计算最少的新建道路的数量, 路径由若干道路首尾相连而成．两条路径相互分离，是指两条路径没有一条重合的道路．但是，两条分离的路径上可以有一些相同的草场．对于同一对草场之间，可能已经有两条不同的道路，你也可以在它们之间再建一条道路，作为另一条不同的道路．

输入输出格式

输入格式：

Line 1: Two space-separated integers: F and R

Lines 2..R+1: Each line contains two space-separated integers which are the fields at the endpoints of some path.

输出格式：

Line 1: A single integer that is the number of new paths that must be built.

输入输出样例

输入样例#1：

输出样例#1：

说明

Explanation of the sample:

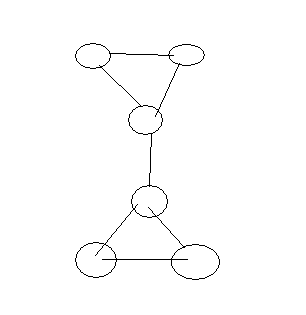
One visualization of the paths is:

1 2 3

+---+---+

   |   |

   |   |

6 +---+---+ 4

/ 5 / / 7 +Building new paths from 1 to 6 and from 4 to 7 satisfies the conditions.

1 2 3

+---+---+

:

6 +---+---+ 4

/ 5 : / :

/ :

7 + - - - - Check some of the routes:

1 – 2: 1 –> 2 and 1 –> 6 –> 5 –> 2

1 – 4: 1 –> 2 –> 3 –> 4 and 1 –> 6 –> 5 –> 4

3 – 7: 3 –> 4 –> 7 and 3 –> 2 –> 5 –> 7

Every pair of fields is, in fact, connected by two routes.

It's possible that adding some other path will also solve the problem (like one from 6 to 7). Adding two paths, however, is the minimum.

做法：

taijan缩点，在缩点后的新图上，如果新点的度为1，那么ans++

最后答案=（ans+1）*2

首先，任意两个点之间都有两条道路，那么任意一个点都要在一个环里

任意一个点都在一个环里，有两个思考方向：

1、没有桥（割边）

2、没有度为1的点

先看1，出现一个桥，补一条边，ans=桥的条数，这种方法是错误的

因为一个n条边的链，它有n-1个桥，但是只需要首尾相连就没有桥

所以我们选择2

这样每两个度为一的点，就连一条边，如果单出一个点就再加一条，所以ans=（ans+1）/2

为什么要在缩点之后的图上呢？直接统计度为一的点的个数不行吗？

看下面这个图就明白了

#include<cstdio>

#include<stack>

#include<algorithm>

#define N 5001

#define M 20011

using namespace std;

int n,m;

int tot=,front[N],to[M],nxt[M];

int dfn[N],low[N],id,bl[N],sum;

int p[M/][],d[N];

stack<int>s;

void add(int u,int v)

{

    to[++tot]=v; nxt[tot]=front[u]; front[u]=tot;

    to[++tot]=u; nxt[tot]=front[v]; front[v]=tot;

}

void tarjan(int u,int pre)

{

    dfn[u]=low[u]=++id;

    s.push(u);

    for(int i=front[u];i;i=nxt[i])

    {

        if(i==(pre^)) continue;

        if(!dfn[to[i]])

        {

            tarjan(to[i],i);

            low[u]=min(low[u],low[to[i]]);

        }

        else low[u]=min(low[u],dfn[to[i]]);

    }

    if(low[u]==dfn[u])

    {

        sum++;

        while(s.top()!=u)

        {

            bl[s.top()]=sum;

            s.pop();

        }

        bl[s.top()]=sum;

        s.pop();

    }

}

int main()

{

    scanf("%d%d",&n,&m);

    for(int i=;i<=m;i++)

    {

        scanf("%d%d",&p[i][],&p[i][]);

        add(p[i][],p[i][]);

    }

    tarjan(,);

    for(int i=;i<=m;i++)

        if(bl[p[i][]]!=bl[p[i][]]) d[bl[p[i][]]]++,d[bl[p[i][]]]++;

    int ans=;

    for(int i=;i<=n;i++)

      if(d[i]==)  ans++;

    printf("%d",ans+>>);

}