【博弈论】【P1288】取数游戏II

传送门

Description

有一个取数的游戏。初始时，给出一个环，环上的每条边上都有一个非负整数。这些整数中至少有一个0。然后，将一枚硬币放在环上的一个节点上。两个玩家就是以这个放硬币的节点为起点开始这个游戏，两人轮流取数，取数的规则如下：

（1）选择硬币左边或者右边的一条边，并且边上的数非0；

（2）将这条边上的数减至任意一个非负整数(至少要有所减小)；

（3）将硬币移至边的另一端。

如果轮到一个玩家走，这时硬币左右两边的边上的数值都是0，那么这个玩家就输了。

如下图，描述的是Alice和Bob两人的对弈过程，其中黑色节点表示硬币所在节点。结果图(d)中，轮到Bob走时，硬币两边的边上都是0，所以Alcie获胜。

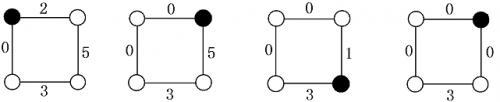
（a）Alice （b）Bob （c）Alice （d）Bob

现在，你的任务就是根据给出的环、边上的数值以及起点（硬币所在位置），判断先走方是否有必胜的策略。

Input

第一行一个整数N（N≤20），表示环上的节点数。

第二行N个数，数值不超过30，依次表示N条边上的数值。硬币的起始位置在第一条边与最后一条边之间的节点上。

Output

仅一行。若存在必胜策略，则输出“YES”，否则输出“NO”。

Sample Input_1

Sample Output_1

YES

Sample Input_2

Sample Output_2

NO

Hint

（N≤20）

Solution

　　博弈论。有如下性质：

　　　定理一：先手决定取数的方向。

　　　　证明：如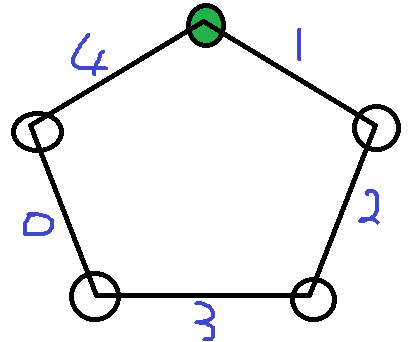图一：（图一）

　　　　　　从绿色点开始取数，不妨设先手想顺时针方向取数，那么只需要把权值为1的边取成0即可。后手只能继续顺时针取数，因为不能取边权0的一侧。

　　　　　　一般的，先手只要将自己想要的方向取成0，那么就可以决定自己取数的方向。

　　　定理2：取数过程的方向是单向的，一旦确定不会折返。

　　　　　证明：

　　　　　　如图一，依然不妨设先手想顺指针取数，那么他先取了边权为1的边，此时后手只能继续顺时针取数，不管他将2取成1还是0，先手如果想继续顺时针取数，那么只需要继续取边权为3的边为0即可，无需考虑后手上一步是怎么取得。因为下一条边取成0之后，无论如何都不会返回上一条边了。

　　　　　　一般的，先手只要把自己经过的边取成0，就可以保证过程单向不会折返。

　　　由定理1、2易推知定理3：在取数过程中，每个人会取到哪个位置是唯一确定的。

　　　由定理2可以推知定理4：在取数过程中，谁的“前进道路”的下一条边是零边谁就会输。

　　　　　证明：由定理2可知方向是单向的。如果前面是0边，则无法往前走，由定理二也无法往后走（只需要上一手的人把上一条边取成0）。于是会输。

　　综合定理1、2、3、4可以知道，只要出发点的取数方向一侧的线段离0边距离为偶数，则必胜，否则必输。由于先手可以选择顺时针或逆时针，所以枚举两个方向，如果有必胜策略则必胜。如果都会输则GG。

Code

#include<cstdio>
#define maxn 25

inline void qr(int &x) {
    char ch=getchar();int f=;
    while(ch>''||ch<'')    {
        if(ch=='-')    f=-;
        ch=getchar();
    }
    while(ch>=''&&ch<='')    x=(x<<)+(x<<)+(ch^),ch=getchar();
    x*=f;
    return;
}

inline int max(const int &a,const int &b) {if(a>b) return a;else return b;}
inline int min(const int &a,const int &b) {if(a<b) return a;else return b;}
inline int abs(const int &x) {if(x>) return x;else return -x;}

inline void swap(int &a,int &b) {
    int c=a;a=b;b=c;return;
}

int n,MU[maxn];

int main() {
    qr(n);for(int i=;i<=n;++i) qr(MU[i]);
    if(MU[]) for(int i=;i<=n;++i) {
        if(MU[i]==) {
            if(!(i&)) {
                putchar('Y');putchar('E');putchar('S');putchar('\n');return ;
            }
            break;
        }
    }
    if(MU[n]) for(int i=n;i;--i) {
        if(MU[i]==) {
            if(!((n-i+)&)) {
                putchar('Y');putchar('E');putchar('S');putchar('\n');return ;
            }
            break;
        }
    }
    putchar('N');putchar('O');putchar('\n');
    return ;
}